一种计算强几何限制自旋模型的量子蒙特卡洛算法的制作方法

本发明属于强关联物理数值技术领域，具体涉及一种计算强几何限制自旋模型的量子蒙特卡洛算法。

背景技术：

强关联系统中由于粒子间的相互作用很强且伴有复杂的量子纠缠，使得体系往往会呈现出新奇的物象，比如自旋液体、高温超导、莫特绝缘体等等。但同时也正由于体系本身的复杂性，我们往往只能借助数值技术进行计算。目前常用的成熟数值技术各有优劣：严格对角化只能计算很小的系统，受到尺寸效应影响巨大；密度矩阵重整化群在（准）一维系统中效果拔群，却难以研究高维体系；量子蒙特卡洛技术受到符号问题限制，难以计算具有量子阻挫的系统。然而可惜的是很多当前科学家关注的新奇物象往往出现在二维、三维的阻挫系统中，使得目前常用的成熟数值技术束手无策。然而很多阻挫体系中的新奇物象，往往可以通过给系统增加一些几何限制而得到，比如由于量子dimer模型中带有很强的几何限制，每个格点属于且仅属于一个最短程的dimer，如图1所示：既不能像(a)所示有空余的格点，也不能像(b)所示一个格点属于多个dimer，更不能像(c)中形成非最短程的dimer。所以体系中往往会出现一些阻挫导致的物相，如z2和u(1)自旋液体以及其他的一些新奇价键固态。量子dimer模型这一类有几何限制的模型，往往没有量子阻挫，但是却可以出现丰富的阻挫物相。对于这一类模型，密度矩阵重整化群类的张量网络方法无法添加block以运作；严格对角化依旧受制于尺寸效应；量子蒙特卡洛也由于几何限制而导致难以有效抽样。本发明提供了一种可以有效抽样，不受制于几何限制的量子蒙特卡洛方法。基于该方法，二维、三维系统的一些新奇物态可以得到有效研究。

技术实现要素：

本发明的目的在于提供一种可以严格计算强几何限制自旋模型的量子蒙特卡洛算法。

本发明提供的量子蒙特卡洛算法，适用于有几何限制的量子自旋模型。

1、以量子dimer模型为例，每个格点属于且仅属于一个最短程的dimer，如图1所示，既不能有空余的格点，也不能一个格点属于多个dimer，更不能形成非最短程的dimer。量子dimer模型的哈密顿量可以写为：

这里，求和表示对晶格里所有的单元方块求和；一个dimer可以理解为端点的两个自旋形成的一个自旋单态，而动能项则可以理解为一个方块内一对平行的dimer的共振。这个看似简单的哈密顿量包含了很强的几何限制，要求每个格点属于且仅属于一个最短程dimer。值得一提的是，这个哈密顿量在v=1的参数点上（rk点），基态是严格可解的。基态的波函数为同一个拓扑类内各个经典构型的等权重叠加，不同拓扑类的权重可以不同。这就是一个共振价键态(rvb)的基态波函数特征，所以这个模型在很多晶格下会出现不同性质的rvb相。由于非对角项是负的，所以这个哈密顿并没有符号问题，不管在任何格子上都可以用量子蒙特卡洛方法来计算。在此模型下，直接选取键的构型来作为基矢，一组构型可以写成|α=|d1,d2,...,dn。当键上有dimer的时候，di取值为1；如果没有dimer，取值为0。

把哈密顿量拆分成方块为单位hp的叠加形式：，这里的p是方块的序号。进一步地，可以把方块的哈密顿量hp拆分成对角算符和非对角算符之和，即hp=h1,p+h2,p。这里脚标1表示对角算符，2表示非对角算符：

在上式的哈密顿量中，配了一个常数np(v+c)上去，这是为了让所有概率为正数。这么做并不影响物理，但是在计算能量的时候要考虑减去这个常数。为了让所有的矩阵元正定，必须满足条件c>min(−v,0)。为了简单方便起见，下文中选取c=1。

2、接下来，把配分函数展开成哈密顿量h的各项级数，并且把h拆分成对角和非对角算符，于是便可以得到一个多项级数展开的求和式。求和的算符脚标可以用sn=[a1,p1],[a2,p2],...,[an,pn]表示。这里的ai∈{1,2}表示算符类型，即1表示对角算符,2表示非对角算符，同时pi∈{1,...,np}表示方块的序号。方便起见，还需要对级数做一个截断，假设保留到h的m阶项，另外，再引入单位算符[0,0]作为一种算符类型。于是可以得到以下配分函数形式：

这个形式和在普通自旋模型方法中是类似的。这里的n表示除了单位算符外的算符数量，即[ai,pi]≠[0,0]的数量。

3、通过对所有构型求内积，可以得到如下的非零矩阵元：

这里的态|others表示这个方块内只有1个或者没有dimer。

4、算符更新。在蒙特卡洛方法中，对于算符列的更新，第一步是插入或者取消一个对角算符，也就是对角更新。本发明算法在对角更新这一步与普通的自旋模型sse算法是类似的，根据metropolis的细致平衡可以给出概率如下：

其中pins表示在原本没有算符（或者说单位算符）的位置插入一个对角算符的概率，而pdel表示在已有对角算符的位置移去这个算符的概率。np表示所有的单元方块数，在插入对角算符时，因为有共np个位置可以插入，所以在分子处要考虑选择概率。同理，选择概率也考虑在逆过程（取消对角算符）时。对角更新应该沿着虚时间逐层扫描，即1,...,m每一层都有该操作。如果遇到非对角算符，则更新构型后继续下一层的扫描。

5、对角更新完成后，一般用集团更新来完成对角算符和非对角算符之间的转化，即算符串中[1,p]↔[2,p]的实现。

针对于不同的自旋模型，有不同的集团构造方法，比如算符圈方法、方向圈方法、团簇型更新等等。但是，由于强几何限制，以上的常规集团更新方法都无法奏效，他们总是难以避免地破坏几何约束。奔放没最主要的结果就是提出了一种有效的集团更新方式，可以自动满足几何限制条件进行抽样。称这种方法叫做“扫描团簇”方法，它引入了“虚时间序”的概念，按照顺序更新。具体方法实现如下：

（1）首先随机任意选取一个算符矩阵元，要求这个矩阵元的两边都是可翻转构型（fp），即方块中有两个平行的dimer。无所谓对角或者非对角的矩阵元，随机选取即可。

（2）矩阵元一侧的方块构型，四条键全部翻转，继而生出四条更新线，注意更新线只能沿着一个虚时间方向顺序生长，直至团簇生成。用更新线在虚时间生长来标记每一个虚时间时刻构型的翻转状态，更新线所到之处键进行翻转。这样按照顺序地扫描各个虚时间层，每扫描到某一层虚时间矩阵元构型的时候，矩阵元的一侧已经被其前端构型生成的更新线所更新。接下来就是讨论另一侧的矩阵元如何更新如图2所示。

（3）每一层的矩阵元更新方式，分为三种情况：

（a）已更新一侧得到了一个新构型，该构型是可翻转的（方块内有2个平行的dimer）。同时待更新一侧的构型是不可翻转的，那么可以有两种更新方式：按照1/2概率选择待更新一侧更新为对角（与已更新侧一致）构型还是非对角（与已更新侧构型相反）构型。如图2中（c）（d）所示，根据不同的选择，生成不同的更新线，继续生长；

（b）已更新一侧得到一个新的构型是不可翻转的，那么待更新一侧只能选择与之一致，生成一个对角矩阵元。如图2中的（a）和（b）以及（e）和（f）所示；

（c）已更新一侧得到了可翻转的新构型，待更新一侧也是可翻转的构型，此时有两种情况：如果除了此矩阵元外没有其他更新线剩余，则团簇生成，不需要继续更新；如果除了此矩阵元外还有其他更新线在生长，那么待更新一侧的4个键全部翻转，生成4条更新线，继续扫描下一层。

当所有更新线走完，生成一个大的团簇，也随即得到了一个新的构型b，它的权重为wb。同时，把翻转前的老构型命名为a，它的权重为wa。值得一提的是，这里不可能像方向圈算法那样边走边更新，因为更新线之间存在着强关联，所有更新线必须一起生长、互相影像，这也决定了它无法如方向圈算法那样让单个的更新线选择如何行走，所以必须让整个团簇生成之后判断是否接受。根据metropolis概率判断是否接受b构型：

这里的pselect(a→b)表示在扫描团簇算法中从构型a转化到构型b的选择概率，即从a走到b的这条途径占从a走到其他构型的所有途径的比例是多少。这其中也包含了上述更新情况中的1号情况，随机选取任意的一个可翻转矩阵元。把构型a中所有的可翻转矩阵元（矩阵元两边的方块都含有一对平行的dimer），即fp的总数记为nfp，同样地，把构型b中可翻转矩阵元的总数记为nfp+∆。则在奔放没算法中，这个接受概率可以简化为：

在温度很低的情况下，第一项nfp/（nfp+∆）≈1，从而paccept(a→b)≈1。在rk点上，任意的新构型能够被接受。这也从另一个角度解释了为什么rk的基态波函数等于所有构型的等权重叠加。

本发明通过引入“虚时间序”的概念，让更新线按照虚时间发展更新，不能“时间倒流”。从而保持世界更新线之间的强关联效应，自动满足几何限制。

目前为止，本发明是全世界第一个不依赖于具体参数、晶格和温度处理强几何限制自旋模型的严格数值方法。

附图说明

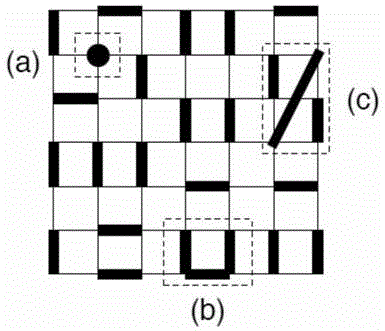
图1：量子dimer模型的几何限制，即每个格点属于且仅属于一个最短程dimer。这里也给出了一些反例，比如:(a)没有dimer的格点，(b)属于多个dimer的格点，以及(c)非最短的dimer。

图2：举例列出一些非零矩阵元构型。更新线所到之处表示该处的键需要翻转。如图(c)和(d)，即使更新出发的构型一致，通过生成不同方式的更新线，可以选择对角算符或者非对角算符。

图3：量子dimer模型的虚时间构型。每一个小图表示某一个特定虚时刻的构型，箭头走向表示虚时间方向。”d”和”n”表示作用在该方块上的对角和非对角算符。(a)和(b)分别表示同一组虚时间构型在团簇翻转前和翻转之后。更新后的图中，空心的小圆圈表示垂直纸面穿过该处键的更新线，也就是说有圆圈的键位处需要翻转。从每一层的虚时间切片看来，回到了经典dimer构型下的经典圈更新方法。

图4：经典dimer构型的圈更新，即每个被圈路经的键位都必须翻转。

图5：扫描团簇算法和对更新算法在三角晶格4×4和4×3格子上与严格对角化（ed）得到的能量之差。

图6：正方晶格上量子dimer模型的关联函数，保留到小数点第三位。实线表示有dimer，虚线表示没有，粗细表示有无dimer的强度。参数选取v=0。

具体实施方式

一个新的算法设计，首先要验证其计算的可靠性，本节所有的结果都在t=0.01的温度下计算。如果要用世界线方法计算量子dimer模型，一般只能用配对更新的方式，即只能翻转面对面的两个算符来更新。这种算法既非常低效又不遍历。在三角晶格中，将扫描算法和配对更新方法做了对比，以严格对角化（ed）的能量为基准做差。在相同的蒙特卡洛步数之下，明显可以看到配对更新离标准能量差距较大，而误差却很小。这是因为配对更新的方式每次只能更新两个算符，这是很局域的，会带来很长的自关联效应。另外也计算了8x8正方格子上的关联函数，与严格对角化得到的结果一致。

本发明通过以虚构时间顺序扫描顶点来维持世界更新线之间的强关联效应，从而保持几何限制。原则上它对量子dimer模型的整个参数区域是有效的。它也是qdm的第一个有限温度qmc方法，它直接对dimer空间进行采样。此外，它适用于任何晶格结构，并可以推广到其他几何限制的模型，如量子圈模型等。