基于信号稀疏表示理论的高精度Gabor时频分析方法与流程

本发明属于信号与信息处理技术，具体涉及一种基于信号稀疏表示理论的高精度gabor时频分析方法。

背景技术：

fourier变换是分析和处理平稳信号最常用的方法，在通讯和自动控制、信号与图像处理、机器视觉等领域有着广泛的应用。然而，由于fourier变换将时间函数变成了频率的函数，该频率函数无局部时间上的频率信息，因此无法表述信号的时频局域性，由fourier变换系数生成的fourier频谱也无法表述信号的频率分量是如何随时间变化的，而频率分量随时间变化的性质恰恰是非平稳信号如语音、雷达信号、生物医学信号等最根本和最关键的性质。

英国物理学家dennisgabor最早发现了fourier变换的这一缺点，从而于1946年提出了在非平稳信号分析和处理中使用时间和频率两个变量对信号进行描述的方法。他将fourier变换的核函数与可时移的高斯窗函数相乘积，构造了一新的可时移和频移的变换核，提出了在联合时频域中将信号展开成一组gauss基函数形式。这一展开形式被后人称为gabor展开，而求解展开系数的式子被称为gabor变换。因此gabor变换与gabor展开构成了一互为逆变换的变换对，成为当今时频分析的主要工具之一。

最初的gabor展开在时间上是连续的、无限长的和非周期的，在提出之后的较长时间里，尽管gabor展开被公认为是有用的，但因为其展开或变换系数计算的困难，应用一直受到限制。造成计算gabor展开或变换系数困难的主要原因是gabor展开的基函数不是正交的，不能用通常的内积规则来计算展开系数。另外，gabor展开与变换是复值形式的，是在复值fourier变换基础上通过引入能够时移和频移的一系列基函数而产生的，其基函数值和变换系数均为复数，对周期的实值离散gabor展开与变换的研究几乎空白。

在对gabor时频分析方法的深入研究中，我们发现由离散gabor变换系数生成的gabor时频谱，即便是取了很大的时频抽样点数，其时频分辨精度也不高，并且极易受其窗函数窗宽的影响，产生这一问题的根本原因，首先是因为由传统的离散gabor变换求得的变换系数其聚集性不高，其次是因为其窗函数受heisenberg不确定原理制约，即其时宽和频宽不可能同时为无限小，二者的乘积大于或等于一常数值(0.25/π)；也就是说，窗函数的时宽和频宽是矛盾的，成反比。这样就对离散gabor变换系数的聚集性产生了很大的影响，有较小时宽的窗函数对应的gabor时频谱时间分辨精度较好但频率分辨精度较差，因为该窗函数的频宽较大；反之，有较大时宽的窗函数对应的gabor时频谱时间分辨精度较差但频率分辨精度较好，因为该窗函数的频宽较小。

技术实现要素：

发明目的：本发明的目的在于解决现有技术中存在的不足，提供一种基于信号稀疏表示理论的高精度gabor时频分析方法，本发明首先基于离散gabor变换窗函数窗宽的大小对变换系数聚集性的影响，求解最佳窗宽的窗函数；其次基于信号稀疏表示理论，求解高聚集性离散gabor变换系数，从而获得高精度gabor时频谱。

技术方案：本发明的一种基于信号稀疏表示理论的高精度gabor时频分析方法，依次包括以下两个步骤：

(1)求解离散gabor变换(dgt)最佳窗宽窗函数；

(2)求解高聚集性dgt系数。进一步的，所述步骤(1)中求解dgt最佳窗宽窗函数的具体内容为：

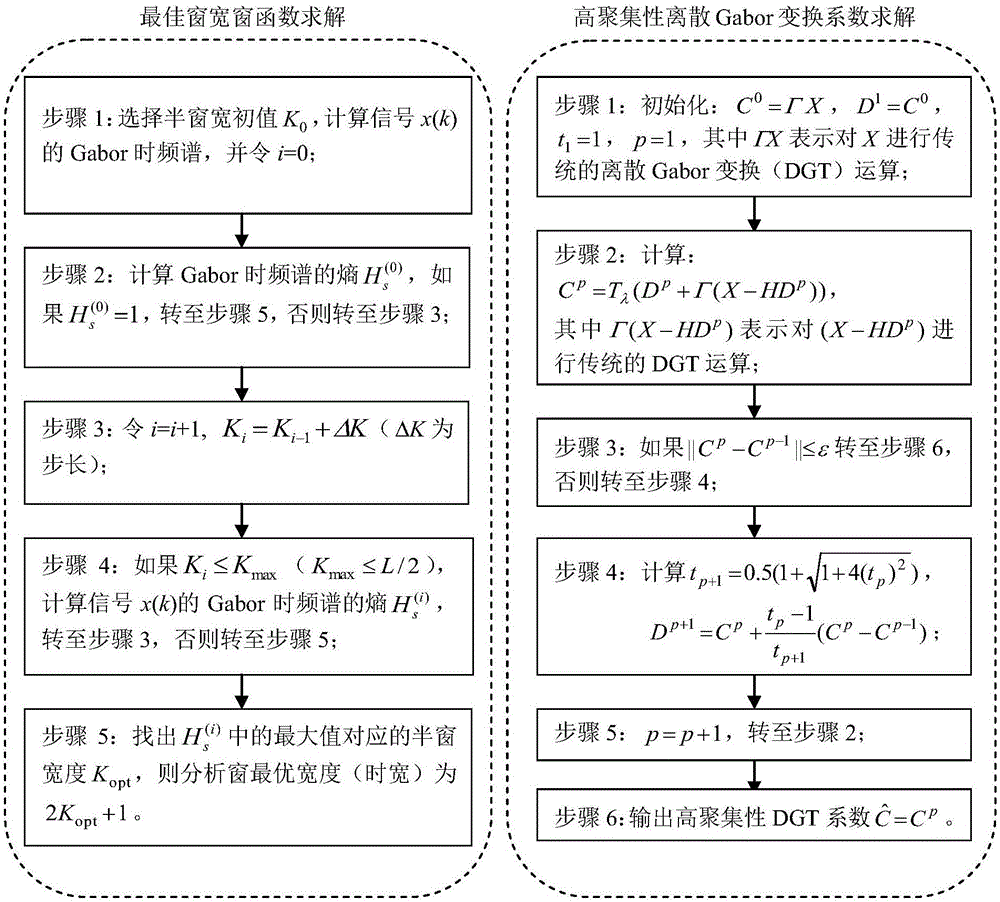
(1.1)选择半窗宽初值k0，计算信号x(k)的gabor时频谱，并令i＝0；

(1.2)计算gabor时频谱香农熵如果转至步骤(1.5)，否则转至步骤(1.3)；

(1.3)令i＝i+1,半窗宽度ki＝ki-1+△k，△k为步长(例如取整数3左右)；

(1.4)如果ki≤kmax且kmax≤l/2，计算gabor时频谱的熵转至步骤(1.3)，否则转至步骤(1.5)；

(1.5)找出中的最大值对应的半窗宽kopt，则分析窗最优宽度(时宽)为2kopt+1；

此处设x(k)表示由一个有限长序列拓展成周期为l的实序列，其离散gabor展开和变换分别为

其中“*”表示复数共轭。上两式中

式中，w＝exp(j2π/n)，m和n分别为时频域中时间和频率的gabor抽样点数，和分别为频率和时间的gabor抽样间隔，稳定的重建条件(完备性条件)是(或mn≥l)；和分别是综合窗h(k)、分析窗γ(k)的周期延伸。满足下列离散双正交条件：

或对偶式：

上两式中在给定综合窗h(k)条件下由(5)式即可求出分析窗γ(k)，反之，在给定分析窗γ(k)条件下由(6)式即可求出综合窗h(k)。为能够获得高分辨率时频谱(增加其时频点数)，取mn>>l(即gabor过抽样率β＝mn/l>>1)，此时综合窗h(k)与分析窗γ(k)高度相似(具有几乎相同的时宽)。

值得注意的是利用上述传统的双正交分析法(包括框架理论法或似正交分析法)得到的离散gabor变换系数c(m,n)其聚集性都不高，并且极易受综合窗(或分析窗)尤其是其窗宽选择的影响，从而造成由变换系数生成的gabor时频谱s(m,n)时频精度也不高。

s(m,n)＝|c(m,n)|²,0≤m≤m-1,0≤n≤n-1(7)

本发明将离散gabor展开式(1)表示成矩阵形式:

x＝hc(8)

式中x为x(k)的l维列向量，c为c(m,n)的mn维列向量，h为由基函数构成的l×mn维矩阵。再将求离散gabor变换系数的式子(2)表示成矩阵形式：

c＝γx(9)

式中γ为由基函数构成的mn×l维矩阵。

所述步骤(1)中，归一化香农熵：

其中ps(m,n)为gabor时频谱s(m,n)的归一化时频分布，s(m,n)＝|c(m,n)|²，且hs∈[0,1]，0≤m≤m-1,0≤n≤n-1；采用高斯函数作为综合窗对信号进行展开，即其中，k为半窗宽。

进一步的，步骤(2)求解高聚集性dgt系数算法1的具体内容为：

(2.1)初始化：dgt系数c⁰＝γx，d¹＝c⁰，t1＝1，p＝1，其中γx表示对x进行离散gabor变换运算；

(2.2)计算c^p＝tλ(d^p+γ(x-hd^p))，其中γ(x-hd^p)表示对(x-hd^p)进行离散gabor变换运算；

(2.3)如果||c^p-c^p-1||≤ε转至步骤(2.6)，否则转至步骤(2.4)；

(2.4)计算

(2.5)p＝p+1，转至步骤(2.2)；

(2.6)输出高聚集性dgt系数

所述步骤(2)中，根据时频变换系数的聚集性与其稀疏性等同关系，并利用线性方程稀疏解算法，将高聚集性离散gabor变换系数求解问题转换成求其稀疏解的最优化问题，即按下式求线性方程组(8)式的稀疏解：

式中λ是一惩罚因子(大于0的正实数)，利用快速迭代收缩阈值算法(fastiterativeshrinkage-thresholdingalgorithm,fista)对上式稀疏解进行快速求解，即：

c^p+1＝tλ(c^p+γ(x-hc^p))

式中p为迭代次数序号，软阈值函数tλ(c)列向量第k项定义为

算法中给定变换系数迭代收敛容限值ε。

有益效果：本发明通过将高聚集性离散gabor变换系数求解问题转换成求其稀疏解的最优化问题，从而提出高聚集性离散gabor变换系数求解算法，本发明对已有的实值线性方程组稀疏解算法进行改进，并利用传统离散gabor变换及其逆变换快速算法加速求解计算。另外，基于gabor时频谱香农熵的窗函数最佳窗宽求取算法，在变换系数的高聚集性约束条件下计算不同窗函数窗宽对应的变换系数聚集性评估值(即gabor时频谱香农熵)，从而找出最佳窗函数窗宽。有了最佳窗宽的窗函数，就可以求出对应的离散gabor变换系数稀疏解，从而获得更高时频精度的gabor时频谱。

附图说明

图1为本发明的整体流程图；

图2为传统离散gabor变换使用较小时宽窗函数产生的gabor时频谱；

图3为传统离散gabor变换使用较大时宽窗函数产生的gabor时频谱；

图4为传统离散gabor变换使用适中(最佳)时宽窗函数产生的gabor时频谱；

图5为本发明中利用离散gabor变换系数稀疏解生成的gabor时频谱(使用了最佳窗宽的窗函数)。

具体实施方式

下面对本发明技术方案进行详细说明，但是本发明的保护范围不局限于所述实施例。

如图1所示，本发明的一种基于信号稀疏表示理论的高精度gabor时频分析方法，其特征在于：包括以下两个步骤：

(1)求解dgt最佳窗宽窗函数；

(2)求解高聚集性dgt系数。

所述步骤(1)求解dgt最佳窗宽窗函数的具体内容为：

(1.1)选择半窗宽初值k0，计算信号x(k)的gabor时频谱，并令i＝0；

(1.2)计算gabor时频谱香农熵如果转至步骤(1.5)，否则转至步骤(1.3)；

(1.3)令i＝i+1,半窗宽度ki＝ki-1+△k(△k为步长)；

(1.4)如果ki≤kmax(kmax≤l/2)，计算gabor时频谱的熵转至步骤(1.3)，否则转至步骤(1.5)；

(1.5)找出中的最大值对应的半窗宽kopt，则分析窗最优宽度(时宽)为2kopt+1；

步骤(2)求解高聚集性dgt系数的具体内容为：

(2.1)初始化：dgt系数c⁰＝γx，d¹＝c⁰，t1＝1，p＝1，其中γx表示对x进行离散gabor变换运算；

(2.2)计算c^p＝tλ(d^p+γ(x-hd^p))，其中γ(x-hd^p)表示对(x-hd^p)进行离散gabor变换运算；

(2.3)如果||c^p-c^p-1||≤ε转至步骤(2.6)，否则转至步骤(2.4)；

(2.4)计算

(2.5)p＝p+1，转至步骤(2.2)；

(2.6)输出高聚集性dgt系数

上述步骤(1)中，为第i次迭代中用于时频分布聚集性度量的香农熵。

上述步骤(2)中，x＝hc，x为x(k)的l维列向量，c为c(m,n)的mn维列向量，h为由基函数构成的l×mn维矩阵，γ为由基函数构成的mn×l维矩阵；λ是一惩罚因子；p为使用快速迭代收缩阈值算法fista求稀疏解过程中的迭代次数序号，ε为变换系数迭代收敛容限值；

所述步骤(1)中，香农熵ps(m,n)为gabor时频谱s(m,n)的归一化时频分布，s(m,n)＝|c(m,n)|²，且hs∈[0,1]，0≤m≤m-1,0≤n≤n-1；采用高斯函数作为综合窗对信号进行展开，即其中k为半窗宽。

所述步骤(2)中，x(k)的离散gabor展开和变换分别为：

这里“*”表示复数共轭，上两式中

其中，w＝exp(j2π/n)，和分别是综合窗h(k)和分析窗γ(k)的周期延伸；

将离散gabor展开式(1)表示成矩阵形式:

x＝hc

式中x为x(k)的l维列向量，c为c(m,n)的mn维列向量，h为由基函数构成的l×mn维矩阵。再将求离散gabor变换系数的式子(2)表示成矩阵形式：

c＝γx

式中γ为由基函数构成的mn×l维矩阵。

接着根据时频变换系数的聚集性与其稀疏性等同关系，并利用线性方程稀疏解算法将高聚集性离散gabor变换系数求解问题转换成求其稀疏解的最优化问题，即按下式求线性方程组x＝hc的稀疏解：

λ为大于0的正实数，然后利用快速迭代收缩阈值法fista对上式快速求取稀疏解即：

c^p+1＝tλ(c^p+γ(x-hc^p))

式中p为迭代次数序号，软阈值函数tλ(c)列向量第k项为：

实施例：

本实施例的具体步骤如下：

假设x(t)＝cos(50cos(πt)+10πt²+70πt)+cos(25πt²+130πt)是一频率随时间变化信号，该信号包含两余弦函数，理论上在时频谱中两余弦函数的频率分别对应一条随时间变化的直线和曲线。

对其进行离散gabor变换，使用较小时宽窗函数产生的gabor时频谱如图2所示，其时间分辨精度较好但频率分辨精度较差。

使用较大时宽窗函数产生的gabor时频谱如图3所示，其时间分辨精度较差但频率分辨精度较好。

若兼顾时间分辨精度和频率分辨精度都不要太差(即最佳时频精度)，可找到一适中(最佳)时宽窗函数，其对应的gabor时频谱如图4所示。也就是说图4是采用传统离散gabor变换能够获得的具有最佳时频精度的gabor时频谱。显然，由传统离散gabor变换系数生成的gabor时频谱，其时频精度极易受窗函数窗宽大小的影响，即便在最佳窗函数窗宽条件下，其对应的gabor时频谱时频精度也不高。

图5所示为本发明中利用离散gabor变换系数稀疏解生成的gabor时频谱(使用了最佳窗宽的窗函数)。显然，由变换系数稀疏解生成的gabor时频谱，其时频精度远高于传统离散gabor变换系数生成的gabor时频谱。

通过上述实施例可以看出，本发明首先解决由传统的离散gabor变换求得的变换系数其聚集性(时频分辨精度)不高的问题，将基于信号稀疏表示理论并依据变换系数的聚集性(时频分辨精度)与其稀疏性等同关系，把传统离散gabor变换求变换系数的问题转换成求其稀疏解的最优化问题；其次解决最佳窗函数窗宽选择问题，在变换系数的高聚集性约束条件下计算不同窗函数窗宽对应的变换系数聚集性评估值，从而找出最佳窗函数窗宽。有了最佳窗宽的窗函数，就可以求出对应的变换系数稀疏解，从而获得更高时频精度的gabor时频谱。本发明丰富和完善了gabor时频分析理论，使之成为信号与图像处理、通讯、机器视觉、模式识别和自动控制等领域更具吸引力的工具。