一种基于拉格朗日-粒子群更新算法的故障诊断方法与流程

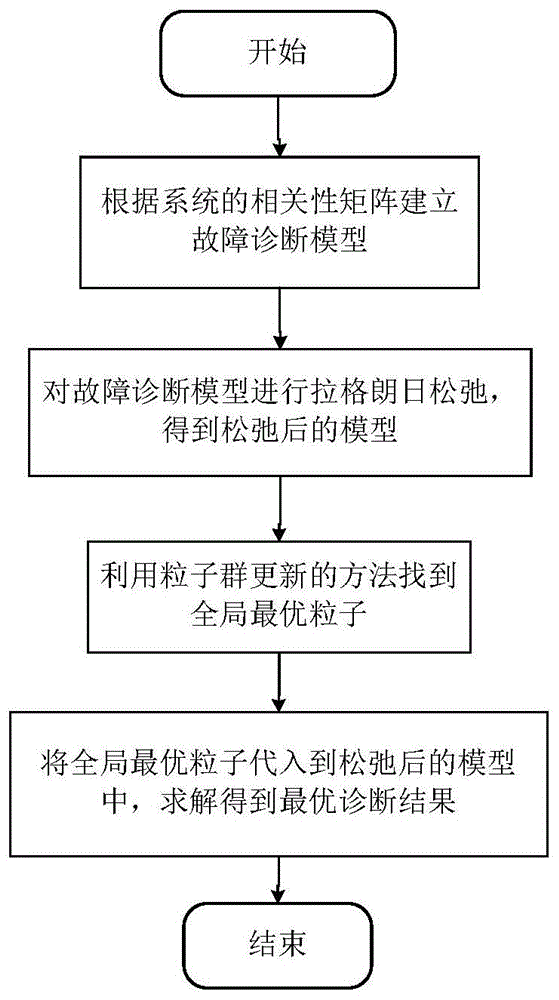
本发明涉及一种基于拉格朗日-粒子群更新算法的故障诊断方法，属于故障诊断领域。技术背景基于模型和测试结果的故障诊断是目前应用较为广泛的故障诊断方法。该方法基于系统的相关性矩阵，采用贝叶斯理论建立其故障诊断模型并使用人工智能算法进行求解。拉格朗日松弛算法属于人工智能算法，已成熟应用于求解基于贝叶斯理论建立的故障诊断模型。但是现有的拉格朗日松弛算法理论分析较为复杂，算法涉及最优解与拉格朗日乘子相互迭代的过程，结构层次不分明，算法中判断和循环较多，编程实现难度较大。目前，尚未发现一种利用粒子群方法更新拉格朗日乘子，对拉格朗日松弛算法进行改进的算法。技术实现要素：本发明的目的是采用粒子群算法对拉格朗日松弛算法进行改进，提出一种基于拉格朗日-粒子群更新算法的故障诊断方法。首先，基于故障-测试相关性矩阵，利用贝叶斯理论构造故障诊断模型；其次，对故障诊断模型进行拉格朗日松弛，得到松弛后的模型；最后，采用粒子群算法更新拉格朗日乘子找到其全局最优解，利用该乘子求解拉格朗日模型得到诊断结果。一种基于拉格朗日-粒子群更新算法的故障诊断方法包括以下4个步骤：步骤1：利用相关性矩阵构造故障诊断模型。根据系统结构和信号流向，利用图论分析得到故障-测试相关性矩阵：其中，fi(i＝1,…m)表示第i个故障；tj(j＝1,…n)表示第j个测试；相关性矩阵d中元素dij取值为1或0，分别表示第i个故障与第j个测试相关或不相关。基于该相关性矩阵，利用贝叶斯后验概率公式，将需要求解的最大后验故障概率转化为系统已知的先验故障概率，得到故障诊断模型：其中，s-为故障集s中去除确认未发生故障的故障集合，a为d矩阵中除去未发生故障的测试列的矩阵再转置得到；pi(i＝1,…,m)为故障fi的先验概率；x为故障向量，表示组件的故障状态，当故障fi发生故障时，xi＝1；反之xi＝0。步骤2：将故障诊断模型进行拉格朗日松弛，得到松弛后的优化模型。将约束条件ax≥e吸收到目标函数zip中，得到进行拉格朗日松弛后的模型为：式中，为拉格朗日乘子；tf为测试未通过的测试列。步骤3：利用粒子群更新方法找到全局最优的拉格朗日乘子λb。流程图如图2所示，包括以下步骤：步骤3.1：根据拉格朗日乘子λ的维数和种群数量，构造初始的拉格朗日乘子种群；步骤3.2：计算种群每个粒子λ的上下界之差的绝对值j；具体方法为：将每个粒子代入到模型(2)中，求解出下界zdw和故障x，再根据故障x构造可行解x′，将可行解x′代入模型(1)求解得到上界zup，计算上下界之差的绝对值j＝|zup-zdw|。步骤3.3：计算每个粒子的适应度函数值其中，k为比例系数。步骤3.4：当本代粒子的适应度函数值ft大于粒子在历史最佳位置时的适应度函数值fb时，即ft＞fb时，更新粒子的历史最佳位置pb＝pt，否则，不更新历史最佳位置；初始历史最佳位置即种群的初始值。步骤3.5：根据所有粒子在历史最佳位置时的函数值，找出其中函数值最大的粒子对应的历史最佳位置，即为本代的全局最优粒子步骤3.6：惯性权重更新wt＝wmax-t(wmax-wmin)/nmax，其中，t为迭代代数；wmax、wmin为惯性权重的最大值和最小值。步骤3.7：更新粒子的速度和位置，第i个粒子在第t+1次迭代中第d维的速度为其中，c1、c2为加速度因子；第t代生成的在0-1之间的随机数。若更新后的速度为负，令以减缓粒子向负方向移动的速度(因拉格朗日乘子λ要求非负)。其中，k1为比例系数；vmax为设定的速度最大值。更新后的位置为若令步骤3.8：判断t是否达到最大迭代次数nmax，即t≥nmax，或者本代的全局最优粒子对应的适应度函数值是否大于等于设定的阈值。若是，执行步骤4；若不是，迭代次数t＝t+1，转步骤3.2。步骤4：利用得到的最优乘子λb代入到松弛后的模型(2)中，求解得到诊断结果xb。以上为基于拉格朗日-粒子群更新算法的故障诊断方法具体实施步骤。本发明的优点在于：(1)本发明能根据适应度函数值从种群中选出最优粒子，粒子的可选范围更广，选取出的全局最优粒子更好，相比于拉格朗日松弛算法求解出的诊断结果精度更高。(2)本发明能发现隐含故障，排除所有可能存在故障的组件，提高了故障诊断的安全性和可靠性。(3)本发明不涉及拉格朗日乘子与故障相互迭代的过程，而是先求解最优拉格朗日乘子，再代入模型求解诊断结果。并且改进后算法只需一次判断，而拉格朗日松弛算法需要三次判断，结构更加复杂。改进后的算法理论分析简单，结构清晰明了，编程易于实现。附图说明图1是基于拉格朗日-粒子群更新算法的故障诊断流程图。图2是拉格朗日-粒子群更新算法的流程图。图3是拉格朗日松弛算法与拉格朗日-粒子群更新算法的对比图。图4是实例中故障为1,5时全局最优粒子适应度函数值随迭代次数的变化图像。具体实施方式以下结合具体的实施例对基于拉格朗日-粒子群更新算法的故障诊断方法作进一步的说明：阿波罗飞船发射前系统相关性矩阵如表1所示。表1阿波罗飞船系统相关性矩阵选取系统中故障的先验概率相等，均为0.1。若系统故障为1,5时，则检测到故障的测试有2,4,6,7,8,9,10,11,12,13,14。算法应当能够根据测试点未通过(检测到故障)的情况求解出故障1,5。步骤1：利用相关性矩阵构造故障诊断模型。构造的故障诊断模型为：其中，s-为故障集s中去除确认未发生故障的故障集合，(在实际计算的过程中，对于确认未发生的故障xi，将其值先取0，其余值仍为未知)，由d矩阵化简后的得到的a如表2所示；系数均为2.1972。表2化简后得到的的矩阵a步骤2：将故障诊断模型进行拉格朗日松弛，得到松弛后的优化模型。进行拉格朗日松弛后的模型为：式中，λi≥0,(i＝1,…,11)为拉格朗日乘子。步骤3：利用粒子群更新方法找到全局最优的拉格朗日乘子λb。步骤3.1：构造初始的拉格朗日乘子种群，种群数量选取50，具体编程时构造50行11列的矩阵，每一行相当于一个粒子，初始种群矩阵元素均为0-1之间的随机数；步骤3.2：计算种群每个粒子λ的上下界之差的绝对值j；具体方法为：将每个粒子代入到模型(2)中，求解出下界zdw(即模型求解出的函数值)和故障向量x。构造可行解向量x′，初始值与故障向量x相等，然后，对故障向量x中不满足约束条件ax≥e的行(即)，将对应的行添加到解向量x′中，最后，对解向量x′中的每一个故障进行判断，如果将该故障去除后仍满足约束条件，则将故障去除。将得到的可行解向量x′代入模型(1)求解得到上界zup，计算上下界之差的绝对值j＝|zup-zdw|。步骤3.3：计算每个粒子的适应度函数值步骤3.4：根据粒子的适应度函数值决定是否更新粒子的位置，初始历史最佳位置即种群的初始值。具体方法为：当本代粒子的适应度函数值ft大于粒子在历史最佳位置时的适应度函数值fb时，即ft＞fb时，更新粒子的历史最佳位置pb＝pt，否则，不更新历史最佳位置。步骤3.5：根据所有粒子在历史最佳位置时的函数值，找出其中函数值最大的粒子对应的历史最佳位置，即为本代的全局最优粒子步骤3.6：惯性权重更新wt＝1.2-0.004t，t为迭代代数。步骤3.7：更新粒子的速度和位置，第i个粒子在第t+1次迭代中第d维(这里速度的与粒子的维数均为11)的速度为其中，第t代生成的在0-1之间的随机数。若更新后的速度为负，令v＝-0.2×e-(v+2)，减缓向负方向移动的速度(因拉格朗日乘子λ要求非负)。更新后的位置为若令步骤3.8：判断t是否达到最大迭代次数200次，即t≥200，或者本代的全局最优粒子对应的适应度函数值是否大于等于1。若是，执行步骤4；若不是，迭代次数t＝t+1，转步骤3.2。最后求解得到的全局最优粒子λb如表3所示。表3故障为1,5时的全局最优粒子λb故障状态全局最优粒子值λb适应度函数值1,55.6156,0,0.8886,2.9666,0,0,0,4.8169,0.6259,0,0.90801.0000全局最优粒子在故障状态为1,5时的适应度函数值随迭代次数的变化图像如图4所示。步骤4：利用得到的最优乘子λb代入到松弛后的优化模型(2)中，求解得到诊断结果向量xb如表4所示。表4故障为1,5时的故障向量xb故障状态报故测试的序号xb对应的故障状态1,52,4,6,7,8,9,10,11,12,13,141,5求解出的故障状态与设定的故障状态相同，说明算法能有效地解决故障诊断问题。将该算法应用于其余双故障状态，求解得到的结果如表5所示。从双故障的诊断结果来看，拉格朗日松弛算法的故障隔离率为88.89％，改进后的算法为91.11％，高于前者的精度。并且当故障为4,6和5,6时，测试的结果相同，改进后的算法能够将故障4,5,6都找出，说明改进后的算法能够发现隐含故障，排除所有故障。表2拉格朗日-粒子群更新算法双故障诊断结果当前第1页12