色噪声环境下基于约束Kalman波束形成方法与流程

本发明属于自适应阵列信号处理领域，具体涉及一种色噪声环境下基于约束Kalman波束形成方法。

背景技术：

近年来，波束形成器被广泛应用于无线通信、语音处理、雷达、声纳、医学成像和其它领域。常见的波束形成器是最小方差无失真响应波束形成器(Minimum Variance DistortionlessResponse,MVDR)。MVDR算法是通过求解输入信号的协方差矩阵进而求取阵列权值，该方法受到采样快拍数的影响较大，当采样快拍数小时，所求的估计协方差和真实协方差之间误差较大，算法的性能下降甚至失效，并且MVDR的收敛速度比较慢。针对收敛速度问题，Kalman滤波算法被应用到波束形成器上，在文献(C.A.Baird,Jr.Kalman-type processing for adaptive antenna arrays.IEEE Int.Conf.Common.(Minneapolis,MN),June 1974,pp.10G–1-10G-44.)中，Baird提出了将Kalman滤波器应用到平稳环境下求解自适应阵列天线的阵列权值上，但是要求输出信号大小必须近似于期望信号，并且估计的不准确性会导致在观测方向上信号的损失。为了解决这个问题，在文献(Y.H.Chen,C.T.Chiang,AdaptiveBeamforming Using the Constrained Kalman Filter.IEEE Trans.AntennasPropag.vol.41,no.11,pp.1576-1580,Nov.1993.)中，Yuan-Hwang等人提出了基于约束Kalman下的自适应波束形成，该方法在原有的Kalman滤波算法的基础上，添加一个沿着观测方向的阵列响应约束到Kalman滤波算法的量测方程上，该算法可以实现非常快的收敛速度，并且能够在干扰方向上形成零陷。Kalman滤波算法由于其高收敛速度和低失调量的优点，被广泛应用到波束形成上。

但是以上波束形成器设计方法通常假定背景噪声为白噪声，但在应用中，实测数据表明，背景噪声并不总是白噪声而是色噪声。在色噪声环境下会导致波束形成算法波形畸变—旁瓣升高和主瓣下降或消失。文献(ZHANG Linrang,LIAOGuisheng,and BAO Zheng.AdaptiveBeamforming in Colored No-ise Environment.ACTA E L EC TR ONI CA SINICA,1998,(12)：75-78.)提出了一种有色噪声环境下克服波形畸变的自适应波束形成方法，但是该方法须知有色噪声的特性。文献(ZHANG Yi,YANGQiong,and TANG Chengkai.An Anti-jamming Algorithm for GPS Adaptive Nulling Antenna Based on Colored Loading[J].Journal ofNorthweaternPolytechnical University,2015，33(5)：874-878.)提出了基于有色对角载入的GPS自适应调零天线抗干扰方法，先对采样协方差矩阵进行扩展，再根据滤波器权值矢量和方向矢量确定一个有色对角矩阵，对采样协方差矩阵进行修改。以上方法都是针对有色噪声下MVDR算法的改进，改进的算法只是能够消除波形畸变，并不能提高算法的收敛速度。色噪声环境下如何改进算法来消除畸变是一个需要解决的问题。

技术实现要素：

本发明的目的在于克服上述技术的缺陷，提出一种色噪声环境下基于约束Kalman波束形成方法。

本发明的目的是这样实现的：

(1)建立阵列天线接收信号模型；

(2)建立白噪声环境下阵列接收数据的状态方程和量测方程，并应用Kalman滤波五组方程，求解出白噪声环境下阵列权矢量；

(3)对色噪声进行一阶马尔科夫建模，将有色量测噪声白化，并在此基础上对阵列接收数据量测噪声进行量测扩充；

(4)将色噪声模型和扩充后的量测带入到Kalman滤波五组方程中，得到新的Kalman滤波方程，最后求解阵列天线权矢量；

所述的步骤(3)包括以下步骤：

(3.1)对量测噪声进行一阶马尔科夫建模，将有色量测噪声白化，建立模型如下

V_m(k+1)＝ψ(k+1,k)V_m(k)+ζ(k).

上式中，相关系数ψ(k+1,k)＝exp(-βT)，β为反相关时间，T为采样时间间隔，ζ(k)为零均值高斯白噪声，并且与v_s(k)不相关；

(3.2)将量测有色噪声白化，对量测矩阵进行扩充得到

Y＝B(k+1)^Hw(k+1)+ψ(k+1,k)V_m(k)+ζ(k).

上式中，B(k)^H为量测矩阵，V_m(k)为量测噪声；将原来的量测方程进行变换得到V_m(k)＝Y-B(k)^Hw(k)，带入到上式中得到

Y-ψ(k+1,k)Y＝[γB(k+1)^H-ψ(k+1,k)B(k)^H]·

w(k)+B(k+1)^Hv_s(k)+ζ(k).

若设则上式可以转化成量测方程的标准形式

Z＝H(k)w(k)+n(k).

由上式可知，新的量测噪声n(k)为高斯白噪声，并且其协方差矩阵为R^*(k)＝E[n(k)n^H(k)]。

所述的步骤(4)包括以下步骤：

(4.1)将扩充后的新的量测方程带入到Kalman滤波方程中可以得到新的权值更新方程

w(k+1)＝K(k+1)[Z-H(k)w(k+1|k)].

上式中，K(k+1)为Kalman滤波增益；

(4.2)求取滤波增益K(k+1)

K(k+1)＝P(k+1|k)H^H(k)[H(k)P(k+1|k)H^H(k)+R^*(k)]^-1.

上式中w(k+1|k)为状态的一步预测，P(k+1|k)为一步预测方差阵；

(4.3)求取w(k+1|k)和P(k+1|k)；

w(k+1|k)＝γw(k).

P(k+1|k)＝γ²P(k)+Q.

其中P(k)为k时刻Kalman滤波方程的误差方差阵；

(4.4)求取P(k+1)

P(k+1)＝[I-K(k+1)H(k)]P(k+1|k).。

本发明具有的有益效果在于：

本发明是在色噪声环境下对波束形成算法的改进。将Kalman滤波算法应用到波束形成上，大大提高了收敛速度，同时低快拍数下波束形成算法波形畸变问题得到了一定的改善；对色噪声进行一阶马尔科夫建模，并对量测矩阵扩充，最后带入到Kalman滤波五组方程中得到新的滤波方程，最终求出阵列权矢量。本发明在低快拍数和色噪声环境下能够分别在期望信号和干扰方向上形成波束和零陷，并且波束图的旁瓣相比原有的算法具有较为明显的改进。

附图说明

图1是均匀线阵模型；

图2是低快拍数下MVDR算法和Kalman滤波算法波束图对比；

图3是MVDR算法和Kalman滤波算法输出SINR随快拍数变化；

图4是单干扰下有色噪声下MVDR算法、Kalman滤波算法和本发明提出的算法的波束图对比；

图5是单干扰下有色噪声下MVDR算法、Kalman滤波算法和本发明提出的算法的输出SINR随快拍数的变化；

图6是三干扰下有色噪声下MVDR算法、Kalman滤波算法和本发明提出的算法的波束图对比；

图7是三干扰下有色噪声下MVDR算法、Kalman滤波算法和本发明提出的算法的输出SINR随输入SNR的变化。

具体实施方式

下面结合附图对本发明做进一步描述。

该方法首先利用约束Kalman的波束形成算法来提高收敛速度；其次对有色噪声进行一阶马尔科夫建模，然后进行量测扩充后建立新的状态方程和量测方程，最后根据扩展后的Kalman滤波方程组求取阵列权值矢量。本文提出的改进后的算法在低快拍数下仍能够在期望信号方向上形成波束和干扰方向上形成零陷，并且对旁瓣有较好的抑制作用。

实现本发明目的技术方案：

色噪声环境下基于约束Kalman波束形成方法，其特征在于：

步骤1：建立阵列天线接收信号模型；

步骤2：建立白噪声环境下阵列接收数据的状态方程和量测方程；并应用Kalman滤波五组方程，求解出白噪声环境下阵列权值量；

步骤3：对色噪声进行一阶马尔科夫建模，将有色量测噪声白化，并在此基础上对阵列接收数据量测噪声进行量测扩充；

步骤4：将色噪声模型和扩充后的量测带入到Kalman滤波五组方程中，得到新的Kalman滤波方程，最后求解阵列天线权矢量。

步骤3中，具体包括以下步骤：

步骤3.1：对量测噪声进行一阶马尔科夫建模，将有色量测噪声白化，建立模型如下

V_m(k+1)＝ψ(k+1,k)V_m(k)+ζ(k).

步骤3.2：将量测有色噪声白化，对量测矩阵进行扩充得到新的量测方程

Z＝H(k)w(k)+n(k).

步骤4中，具体包括以下步骤：

步骤4.1：将扩充后的新的量测方程带入到Kalman滤波方程中可以得到新的权值更新方程

w(k+1)＝K(k+1)[Z-H(k)w(k+1|k)].

步骤4.2：求取滤波增益K(k+1)

K(k+1)＝P(k+1|k)H^H(k)[H(k)P(k+1|k)H^H(k)+R^*(k)]^-1.

步骤4.3：求取w(k+1|k)和P(k+1|k)。

w(k+1|k)＝γw(k).

P(k+1|k)＝γ²P(k)+Q.

步骤4.4：求取P(k+1)

P(k+1)＝[I-K(k+1)H(k)]P(k+1|k).

步骤1：建立阵列天线接收信号模型；

考虑M个阵元组成的均匀线阵，如图1所示，假设阵元间各向同性并忽略阵元间互耦作用，阵元间距d为1/2λ，其中λ＝c/f，c为光速，f为入射信号的频率。则接收信号模型可表示为

X(t)＝as(t)+j(t)+n(t). (1)

上式中，j(t)为干扰信号，n(t)为高斯白噪声，s(t)为期望信号的大小，a为期望信号的导向矢量，可以写成

a＝[e^{j2πdsinθ/λ}...e^{j2π(M-1)dsinθ/λ}]. (2)

假设期望信号和干扰信号互不相关并且都为平稳信号，则天线阵列所接收信号的协方差矩阵定义为

上式中，R_s＝E[s(t)s(t)^H]为期望信号的协方差矩阵，R_j为干扰的协方差矩阵，I为M维单位阵，为阵元噪声功率，(·)^H代表矩阵共轭转置。在实际中，上式的协方差矩阵无法获得，可以根据信号的时间平稳特性，由采样快拍数据得到其最大似然估计值，表示为

R_X＝X(t)X^H(t)/K. (4)

步骤2：建立白噪声环境下阵列接收数据的状态方程和量测方程，并应用Kalman滤波五组方程，求解出白噪声环境下阵列权矢量；

针对传统的波束形成器收敛速度慢的问题，将Kalman滤波器应用到波束形成上，大大提高了算法的收敛速度，并且稳态失调较小。

为了方便后面的推导，引进了输出信号与零信号的均方差(MSE)，表示为

MSE＝E[|0-X^H(k)w(k)|²]＝w^HR_Xw. (5)

因此，使波束形成器输出功率最小等价于使上式中MSE最小。同时波束形成器的约束函数可以表示为

st.w^Ha＝1. (6)

要利用Kalman滤波器来解决式(6)中阵列天线的约束函数，需要建立状态方程和量测方程。波束形成器可以描述成阵列权值w满足一阶马尔科夫过程的滤波器。因此阵列权值更新方程建立如下

w(k+1)＝γw(k)+v_s(k). (7)

上式中，γ式模型中的固定参数，v_s(k)为系统噪声，假定为零均值高斯白噪声，并且协方差矩阵为其中I为单位矩阵，下标“s”代表状态方程。因此，式(7)给出了最优权值状态方程。由式(6)中约束函数可以得到Kalman量测方程如下表示

上式可以写成矩阵形式，表示如下

Y＝B(k)^Hw(k)+V_m(k). (9)

其中，Y＝[0 1]^T，量测矩阵可以表示为

量测噪声可以表示为

其中v₁(k)和v₂(k)分别为残余误差和约束误差，下标“m”表示量测方程，v₁(k)和v₂(k)均为零均值高斯白噪声，其协方差矩阵可以表示为

在平稳环境下，由于最优约束权值矢量一直是一个常矢量，因此约束Kalman算法的真实模型过程方程，即一步预测方程可以表示为

w(k+1|k)＝γw(k). (13)

由式(13)和量测方程(9)可知，约束Kalman滤波算法最小化真实权值矢量与估计权值矢量之间的误差并在观测方向上保持无畸变。Kalman滤波算法的一步预测协方差矩阵记为

P(k+1|k)＝γ²P(k)+Q. (14)

Kalman滤波算法的估计权值矢量表示为

w(k+1)＝w(k+1|k)+K(k+1)[Y-B^H(k+1)w(k+1|k)]. (15)

上式中Kalman增益K(k+1)可以通过下式求取

K(k+1)＝P(k+1|k)B(k+1)[B^H(k+1)P(k+1|k)B(k+1)+R]^-1. (16)

其中用于计算一步预测协方差矩阵的滤波方差阵P(k)可以记为

P(k)＝[I-K(k)B^H(k)]P(k|k-1). (17)

上述参数中，γ和是状态方程必须选定的参数，当外界环境发生变化时能够按照系统模型变化求解最优权值，它们的功能可以从一步预测误差方差阵看出，当这些参数增大时，Kalman滤波器给当前数据更大的权重，保证能够更好的跟踪环境。对于非平稳环境，γ值的典型选取为稍微比1大的值。尽管这个值的选取使状态方程(7)不平稳，但是滤波器的观测环境的平稳性可以通过观测条件保证。的典型值一般选取这也就是说权值的每个元素的变化范围为0.01。这里说明一下，的值越大，表明环境的变化越迅速。对于平稳环境来说，最优权值不随时间发生变化，因此，在这种情况下，可以选择γ＝1，

从量测方程的第一行可以得到，的选取必须同阵列天线的最优输出功率的规则相同，后者的功率可以粗略的估计为σ²和分别为期望信号和入射信号中噪声功率。w为波束形成器的最优权值矢量。值得我们注意的是波束形成器对的选取并不敏感，主要原因是，权值矢量范数的选取是由滤波器选择的，因此波束形成器的输出功率是与的值是相匹配的。但是的取值必须选择很小(比如，)，这样的话，系统的稳健性具有较高的精度。

上述算法中，系统噪声v_s(k)和量测噪声V_m(k)均假设为高斯白噪声，但是在实际应用中，许多系统的干扰和量测噪声均为有色噪声，此时应用Kalman滤波算法求解波束形成器的阵列权值并不是最优的权值，并且与最优权值存在误差，会导致算法性能下降甚至不能形成波束。

步骤3：对色噪声进行一阶马尔科夫建模，将有色量测噪声白化，并在此基础上对阵列接收数据量测噪声进行量测扩充；

步骤3.1：对量测噪声进行一阶马尔科夫建模，将有色量测噪声白化，色噪声模型；

在原有的Kalman滤波算法的基础上，对系统进行分析，可以得到阵列天线模型系统中的输入的有色噪声可以等价于量测噪声，为保证量测噪声始终为白噪声序列，在应用Kalman滤波方程之前必须预白化有色噪声V_m(k+1)。通过对量测噪声进行一阶马尔科夫建模，将有色量测噪声白化，建立如下模型

V_m(k+1)＝ψ(k+1,k)V_m(k)+ζ(k). (18)

其中相关系数

ψ(k+1,k)＝exp(-βT). (19)

式(19)中，β为反相关时间，T为采样时间间隔，式(18)中ζ(k)为零均值高斯白噪声，并且与v_s(k)不相关。

步骤3.2：将量测有色噪声白化，对量测矩阵进行扩充得到新的量测方程；

量测有色噪声白化常用的处理方法为观测增广法(差分法)，通过增广观测矩阵Y，量测矩阵B(k)^H和量测噪声V_m(k)，将式(9)中的量测方程转化成新的量测方程。将(18)式代入(8)式可得

Y＝B(k+1)^Hw(k+1)+ψ(k+1,k)V_m(k)+ζ(k). (20)

由量测方程(9)式可得

V_m(k)＝Y-B(k)^Hw(k). (21)

将上式代入(20)式中可得

Y-ψ(k+1,k)Y＝[γB(k+1)^H-ψ(k+1,k)B(k)^H]w(k)+B(k+1)^Hv_s(k)+ζ(k). (22)

若设(22)式被转化成量测方程的标准形式

Z＝H(k)w(k)+n(k). (23)

由上式可知，新的量测噪声n(k)为高斯白噪声，并且其协方差矩阵为

R^*(k)＝E[n(k)n^H(k)]

＝E{[B(k+1)^Hv_s(k)+ζ(k)][B(k+1)^Hv_s(k)+ζ(k)]^H}

＝B(k+1)^HQ(k)B(k+1)+R_ζ. (24)

步骤4：将色噪声模型和扩充后的量测带入到Kalman滤波五组方程中，得到新的Kalman滤波方程，最后求解阵列天线权矢量。

步骤4.1：将扩充后的新的量测方程(23)和状态方程(7)带入到Kalman滤波方程中可以得到新的权值更新方程

w(k+1)＝K(k+1)[Z-H(k)w(k+1|k)]. (25)

上式中K(k+1)为Kalman滤波增益。

步骤4.2：求取滤波增益K(k+1)

K(k+1)＝P(k+1|k)H^H(k)[H(k)P(k+1|k)H^H(k)+R^*(k)]^-1. (26)

(25)式中w(k+1|k)为状态的一步预测，(26)式中P(k+1|k)为一步预测方差阵。

步骤4.3：求取w(k+1|k)和P(k+1|k)。

w(k+1|k)＝γw(k). (27)

P(k+1|k)＝γ²P(k)+Q. (28)

上式中P(k)为k时刻Kalman滤波方程的误差方差阵，描述的是真实的阵列权值和估计得到的阵列权值的误差的大小。

步骤4.4：求取P(k+1)

P(k+1)＝[I-K(k+1)H(k)]P(k+1|k). (29)

由以上方程可以求得基于有色噪声下的Kalman滤波波束形成器的阵列权值，该阵列权值的求取过程中考虑了有色噪声对阵列权值的影响，波束形成器的性能能够得到一定程度上的改善。

下面将所提的色噪声环境下基于约束Kalman算法与现有的MVDR算法和约束Kalman算法比较，比较这些算法的在色噪声环境下的性能。

相比现有的MVDR算法，Kalman滤波算法由于本身具有很快的收敛速度，能够使算法输出迅速达到收敛。但是在色噪声环境下，无论是Kalman滤波算法还是MVDR算法，都会出现波形畸变问题-主瓣偏移和旁瓣上升，算法的性能下降。本专利提出的方法，考虑到色噪声对算法性能的影响，对色噪声进行建模，然后对Kalman滤波方程进行扩充，从根本上解决了色噪声对算法性能的影响。因此本专利提出的方法相比其它两种算法在色噪声环境下的性能更优。

本发明的效果可通过以下仿真说明：

(一)仿真条件与内容：

1、低快拍数下波束形成器的性能分析

由于空间媒介不均匀等因素的原因，导致信号在传播过程中出现损失，可以用一个方差为0.04的高斯白噪声来修正。假设信号传播过程中的噪声为高斯白噪声，均值为0，方差为0.04。并且选取γ＝1，P(0)＝αI,其中α值为常值，w(0)＝0，

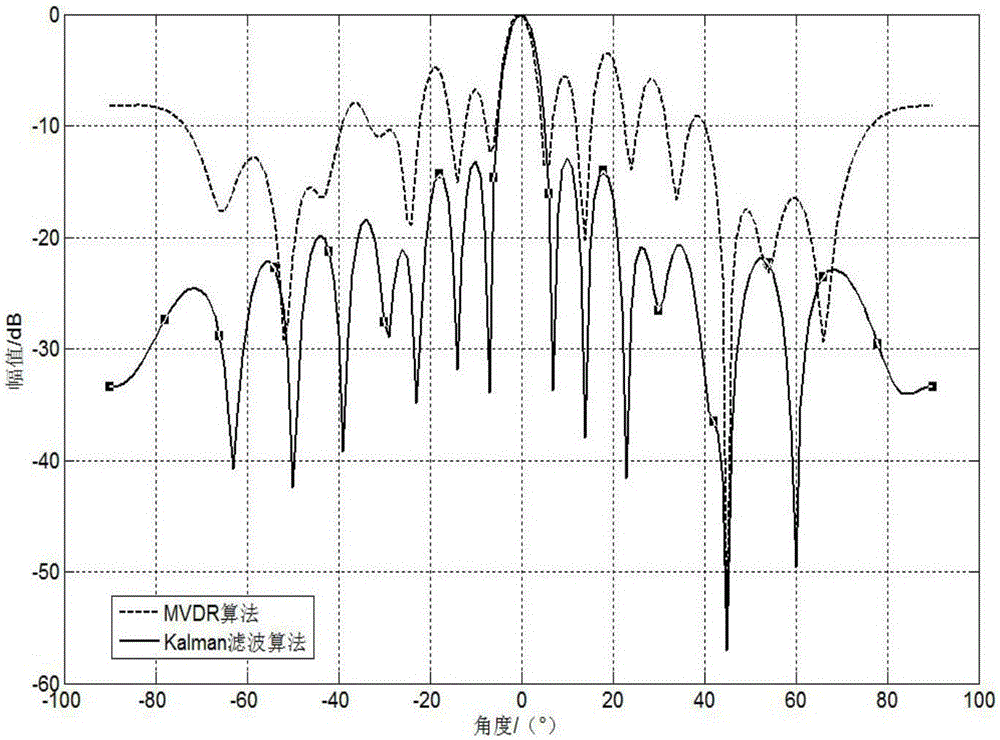
图2是在低快拍数Kalman滤波算法和传统的MVDR算法的输出波束图。从图中可以看出，在快拍数为30时，MVDR算法的输出波束图中主瓣有略微偏移并且旁瓣发生严重的升高。而采用Kalman滤波算法不仅能够在干扰方向上形成较深的零陷而且还能够在期望方向上形成较好的主波束。因此我们可以得到，在低快拍数下，MVDR算法的性能下降，而Kalman滤波算法仍然具有较好的性能。

图3是两种算法随着快拍数不同输出信干噪比(SINR)的变化，从图中可以看出两种算法最终的输出SINR几乎相同，但是Kalman算法在迭代次数较少时，输出SINR仍然较高，并且在快拍数10以内时仍然具有较高的输出SINR为-10dB左右。在快拍数变换范围内Kalman滤波算法的输出SINR几乎保持稳定，而MVDR算法在快拍数低于40左右时，输出SINR值随快拍数变化迅速，在低快拍数时输出SINR可以达到较低值-24dB，在快拍数为50时达到稳定值为-10dB左右。因此可以得出在低快拍数下，MVDR的算法性能受到很大的影响，但是当迭代次数增加时，算法的性能也在随之增加，但是当快拍数达到一定值时，算法的输出SINR保持不变；而Kalman滤波算法在快拍数为10左右时就已经达到稳定，输出的SINR几乎不随快拍数发生改变。因此，从算法稳定性和收敛速度来看，Kalman滤波算法都具有一定的性能优势。

从以上的仿真中我们可以得到，利用基于Kalman滤波下的波束形成算法能够有效地提高算法的收敛速度，在快拍数为十几次时算法就已经达到稳定，并且算法的性能相比MVDR算法来讲，具有一定的优势。因此，可以利用基于Kalman滤波下的波束形成算法来提高低快拍数下算法的收敛速度。

2、低快拍数和色噪声环境下的波束形成器的性能分析

仿真中输入信号噪声选取有色噪声，参数值的选取γ＝1，P(0)＝αI,其中α值为常值，w(0)＝0，有色噪声一阶马尔科夫系数为ψ(k+1,k)在仿真中为常值。

图4是在有色噪声环境下，三种算法：本文所提出的算法，Kalman滤波算法和MVDR的波束图。从波束图中我们可以得到，在有色噪声环境条件下，MVDR算法虽然能够在干扰方向上形成零陷，但是不能在期望方向上形成波束，并且波束图中旁瓣增益上升；Kalman滤波算法虽然能够在干扰方向上形成零陷，也能够在期望方向上形成主波束，但是主波束和旁瓣峰值的差距较小，旁瓣增益明显上升，算法的性能有所下降；而本文提出的改进的算法不仅能够形成主波束，并且能够降低旁瓣增益，并且在干扰方向上还能形成零陷。从以上仿真结果图可以得到，本文提出的改进的算法在有色噪声环境下系统的性能可以得到很大的改善，明显优于Kalman滤波算法和MVDR波束形成算法。

图5是对改进的算法的输出SINR的仿真图，从图中可以看出，在有色噪声环境下，本文提出的算法最终的输出SINR为-16dB左右，并且在迭代次数较少时，输出SINR就已经达到稳定；而Kalman滤波算法的最终输出SINR为-22dB左右，并且在20次迭代以后输出SINR趋于稳定，MVDR算法的最终输出SINR为-23dB左右，并且在60次迭代以后输出SINR趋于稳定。从而可以得出本文的算法在有色噪声环境下输出SINR相比其他两种算法较高，并且达到稳定所需的迭代次数更少。

图6是三干扰有色噪声下算法的波束图，从图中可以看出，三种算法均能够在干扰方向上形成较深的零陷，但是MVDR算法和Kalman滤波算法不能够在期望方向上形成波束，并且旁瓣相对较高，而本文提出的算法能够在期望方向上形成主波束，并且有效的抑制了旁瓣增益。因此，从此图中可以得出，在三个干扰情况下，本文所提出的算法相比其他两种算法性能较好。

图7是输出SINR随输入SNR的变化，从图中可以得出SINR随着SNR变化近似成线性变化，并且相比MVDR算法和Kalman滤波算法来说，本文提出的算法在相同的SNR时，输出SINR较大，从侧面说明了本文算法的优越性。