用于物品的序列化并从序列化物品恢复数据的方法和系统与流程

1.本发明涉及物品的安全编码以实现物品的识别、认证以及跟踪和追踪的技术领域，具体地，涉及用于物品的序列化的方法以及用于物品的序列化的相应系统。


背景技术：

2.多年来，伪造消费品，特别是药物产品，已成为巨大的问题，导致全球市场上的大量低质量危险产品和制造商相当大的收入损失。
3.解决伪造问题的当前解决方案涉及物品序列化和/或标号序列化，其在于在一系列产品、包装、邮票等上印刷唯一码，以能够唯一地标识各单独的产品。通常，码是由对与物品相关联的唯一(序列)号的加密而产生的符号序列，例如如字形、字符、数字等。该唯一序列号实际上指定给定系列的物品内的物品次序(例如，生产线中物品的次序)，从该方面来说，序列号对应于序数。这种唯一序列号的加密的主要目标是隐藏物品的实际顺序以防止伪造者容易地猜出序列号的可信序列(对应于连续物品)。
4.例如，wo2018204319a1描述了对产品的跟踪和认证，诸如存储在泡罩或类似包装中的药物片剂和其他元素，以验证其真实性。由药物产品在包装中的物理属性和位置定义的产品序列被加密并用于利用编码来标记包装。
5.通常，序列化不具有同步问题，各个产品/物品/标签使用适当的触发器或编码器来接收一个唯一的码。通常，可以从生产线中自动地排出错误印刷的产品。这种经典的序列化仅在各个物品被严格标记有其唯一码而没有错误时才工作良好。
6.然而，在一些情形下，可能发生线性不同步，即，码在物品内失准(未正确同步)，导致码在连续物品之间分开，使得一个物品可能具有与下一码的开头级联的先前码的末尾。在这种情况下，经典的序列化不能对码进行解密以找到正确的序列号。线性失准可能由于各种技术原因而发生，诸如在箔上施加预标记，而箔随后在被施加到物品上时在严格控制切割的位置的情况下被切割。例如，一批物品的序列号可以顺序地印刷在连续条带(通常为纸)上，并且随后被切割成与要施加在物品上的码长度相对应的长度片段：由于在切割阶段可能的偏移，施加在给定物品上的片段可能包括相应码的仅一部分和相邻码的一些部分。对于具有序列化安全线的纸币尤其如此：在连续的线上按顺序印刷经编码的序列号，并且这个线被切割成长度通常对应于纸币宽度的片段，并且各个片段被施加(或插入)到相应的纸币上，这具有可能的偏移问题。线在纸币上的横向定位甚至也可能变化。在一些情形下，由于移动物品的高速度、复杂的配准机制的缺失、或者配准的机械不可能性，配准可能是困难的。在任何情况下，线性失准使得典型的序列化是不可能的，从而危害编码物品的后续识别和/或认证(这种失准的切割也可能发生在采集和读取阶段)。
7.示例涉及作为认证特征插入到许多央行的纸币中的安全线，如图11所示。这种线由大的聚合物或金属箔制成，并用不变的印刷进行标记。箔在大辊上连续地被切割并分成线，这些线在安全纸的制造过程中结合到安全纸中。在印刷之后，线最终仅在纸币内的末端被切割。由于线性配准的缺失，不可能进行典型的序列化。因此，安全线当前不以该方式使
用。
8.因此，本发明的目的是提供一种用于物品的序列化的方法和相应的系统，其将允许线性不同步-恢复性编码并且使得能够在任何情形(包括码配准困难或不可能时的情形)下应用适当的序列化。
9.由于本发明，上述药物泡罩现在可以在被切割并用于药丸包装之前被序列化。如图12所示，纸币的安全线可以受益于本发明并且可以被序列化。更具体地，印刷在安全线上的连续码流现在可以使两个不同的纸币永不携带相同的铭文，并且因此这些纸币可以被唯一地认证。此外，不同步-恢复性将使得它们在任何情形下可读。这样的附加安全特征可以是人可读且机器可读的。


技术实现要素：

10.根据一个方面，本发明涉及一种用于物品的序列化的方法，包括：
[0011]-使用加密密钥k来加密各个物品的唯一序列号以获得相应的唯一码，以及
[0012]-用各个物品的相应的唯一码来标记该物品，
[0013]
其中，各个唯一码具有长度l并且被包括在具有长度l’的符号串中，所述符号串被标记在相应的物品上，并且其中，l’大于l。
[0014]
符号串中的符号可以包括选自人类可读字符和机器可读符号的图形符号。符号串中的这些符号可以从字形集合中选择，优选地从字母表、字母数字或数字符号中选择。
[0015]
根据上述方法的变型，唯一码以偏移存在于符号串中，其中l’大于或等于(2l-1)。在另一变型中，唯一码以偏移存在于符号串中，其中l’小于(2l-1)。
[0016]
在上述方法中，唯一码在符号串中的偏移优选地通过以下方式来进行：对于唯一码中的符号的不同位置应用不同的字母表，或者在连续的唯一码之间应用标记，其中该标记选自间隔、特殊标志或框。也可能不使用偏移的指示符，即，对于所有符号，不使用标记并且使用相同的字母表。
[0017]
物品上的符号串的上述标记可以包括直接标记或印刷、应用预印刷标号或激光雕刻。可以通过应用块加密或与格式保留加密(fpe)组合的块加密来进行对物品的序列号进行加密以获得唯一码。
[0018]
可替代地，可以通过基于自同步的密文反馈的流加密来进行对物品的序列号的加密以获得唯一码，其中序列号的符号被以具有格式保留加密(fpe)的流密码结构逐一加密。密文反馈(“cfb”)意味着一个符号的加密取决于一个或若干先前加密的符号。此外，物品上标记的符号串的最小长度l’可以等于(l+k)，k》0是反馈长度，该反馈长度包括所述唯一码的长度l之外的若干字符或至少一个符号。在该变型中，优选地通过将不同的字母表用于唯一码中的符号的不同位置或者在码的开头处使用特定符号来指示偏移。
[0019]
根据另一方面，本发明涉及一种用于根据上述序列化方法从物品上标记的符号串恢复唯一码和相应序列号的解密方法，包括：
[0020]-读取物品上标记的具有长度l’的符号串；
[0021]-基于解密密钥k’，对在所述物品上读取的具有长度l’的所述符号串内具有从0到l-1的偏移的、具有长度l的符号块进行解密，其中l’大于l；
[0022]-对于与具有长度l的块相对应的各个序列号候选n，计算前一序列号n-1和下一序
列号n+1；
[0023]-用加密密钥k分别对序列号n-1和序列号n+1进行加密，分别获得表示为符号串的前一序列号候选和下一序列号候选；
[0024]-逐符号地将所述前一序列号候选与具有长度l’的符号串的相应左侧部分进行比较，并且逐符号地将所述下一序列号候选与具有长度l’的符号串的相应右侧部分进行比较，
[0025]
其中，
[0026]
如果所有被比较的符号匹配，则从读取的符号串中恢复出正确的唯一码和相应的正确的序列号n；以及
[0027]
如果针对偏移至少一个符号比较失败，则没有序列号对应于所述偏移。根据另一方面，本发明还涉及一种用于物品的序列化的系统，包括：
[0028]-存储器和处理器，该存储器与该处理器一起被配置为使该系统使用存储在该存储器中的加密密钥k来对各个物品的序列号进行加密以获得相应的唯一码，以及
[0029]-标记装置，其连接至该处理器并且适于将从该处理器接收的唯一码标记在物品上，
[0030]
其中，该系统被配置为将具有长度l的各个唯一码包括到具有长度l’的符号串中，其中，l’大于l，并且被配置为将符号串标记在相应物品上。
[0031]
存储器连同处理器可以被配置为使系统应用与格式保留加密(fpe)组合的块加密或基于自同步反馈的流加密。
[0032]
可替代地，存储器连同处理器可以被配置为使系统应用格式保留加密(fpe)，其中序列号的密码被以流密码结构逐一加密。
[0033]
根据另一方面，本发明还涉及一种系统，该系统用于如上所述由用于物品的序列化的系统从物品上标记的符号串恢复唯一码和相应序列号，该系统包括配备有存储器单元的处理单元和读取器，其中该读取器被适配成读取物品上标记的符号串并且将所读取的符号串存储在该存储器单元中，并且该处理单元被配置为使该系统进行以下操作：
[0034]-基于存储在存储器单元中的解密密钥k’，对存储在存储器单元中的具有长度l’的符号串内具有从0到l-1的偏移的、具有长度l的符号块进行解密，其中l’大于l；
[0035]-针对与具有长度l的块相对应的各个序列号候选n，计算前一序列号n-1和下一序列号n+1；
[0036]-用加密密钥k分别对序列号n-1和序列号n+1进行加密，并且分别获得前一序列号候选和下一序列号候选；
[0037]-逐符号地将前一序列号候选与具有长度l’的符号串的相应左侧部分进行比较，并且逐符号地将下一序列号候选与具有长度l’的符号串的相应右侧部分进行比较，
[0038]
其中，
[0039]
如果所有比较的符号匹配，则系统适于传送指示从所读取的符号串中恢复出正确的唯一码和相应的正确的序列号n的信号；以及
[0040]
如果针对偏移至少一个符号比较失败，则没有序列号对应于所述偏移。
[0041]
在下文中，将参考附图更全面地描述本发明，其中，贯穿不同的附图，相同的附图标记表示相同的元素，并且在附图中，示出了本发明的突出的方面和特征。
附图说明
[0042]
图1例示了4字符长度码(长度l＝4的码的符号)的7个印刷字符(长度l’＝7的级联串的符号)的示例。
[0043]
图2例示了4字符长度码(l＝4)的6个印刷字符(l’＝6)的示例。
[0044]
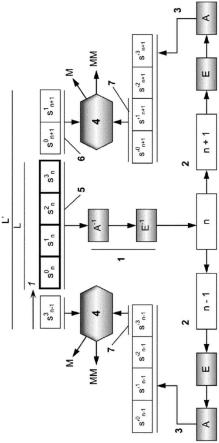
图3是用于解密具有比实际序列长度更长的印刷码的序列号的方法的示意图。
[0045]
图4是在当l’小于2l-1时可能发生的l’字符内不存在l长度码的情况下解密序列号的方法的示意图。
[0046]
图5例示了使用格式保留加密来进行序列化。
[0047]
图6例示了对于4个字符长度(l＝4)码和3个字符长度(k＝3)密文反馈，使用流密码格式保留加密以进行序列化。
[0048]
图7例示了序列化解密方案，其需要至少l’＝l+k个印刷字符来适当地对l个字符进行解密。
[0049]
图8是流密码序列化加密的示意图，其中l’＝l+k+t，t是可选的额外长度，即t≥0(这里：t＝1并且l’＝8)。
[0050]
图9例示了对字符的流密码序列化解密的示例。
[0051]
图10示出了由线性印刷的迷你1d/2d图案构成的专有条形码/符号系统的示例，各个图案表示字母表的符号。
[0052]
图11例示了整合到许多国家的纸币中的常规安全线，其示出了它们的铭文沿其长度的不同步以及变化的横向定位。
[0053]
图12例示了用线性不同步-恢复性序列化标记的安全线，该安全线可以用作纸币的附加认证特征。
具体实施方式
[0054]
序列号是与单个物品相关联的唯一编号。序列号对应于属于序列号集合的序数，该序数以已知序列(诸如0、1、2、3、4、
……
、n-1、n、n+1、
……
、m-1)被逻辑排序：该集合总共包含m个不同的序列号，其中m大于或等于必须被标记的物品的总数(例如，生产批量的物品的总数)。因此，各个物品唯一地与序列号相关联，诸如序列号n与第n个物品相关联、n+1与第(n+1)个物品相关联、等等。序列号可以以任何基数表示，诸如十进制或二进制：编码这些m个不同的序列号所需的最小位长度l
bin
是l
bin
＝ceil(log2(m))，或最小十进制数位长度l
dec
是l
dec
＝ceil(log
10
(m))(其中log2(.)和log
10
(.)分别是以2为底和以10为底的对数，并且ceil(.)是大于或等于整数的最小值)。
[0055]
然后，对这些序列号进行加扰(例如，加密)以隐藏其实际顺序，以防止潜在的伪造者容易地从几个已知的序列号猜测序列号的连续。为此目的，使用应当保密的加密密钥k用加密算法对序列号进行加密，得到加扰序列号，该加扰序列号将被转换/格式化为编码数字或码，以在物品上标记。由于加密是一对一可逆的，因此在序列号和加扰序列号(即码)之间存在双射关系：后者也是唯一的，并且各个原始序列号可以通过用与用于加密的密钥k相对应的解密密钥k’对加扰序列号进行解密来恢复。在不知道解密密钥k’的情况下加扰序列号的排序对于伪造者而言是不可预测的。加扰的格式化序列号可以用除了未加扰的格式化序列号之外的其他基数来表示，但是这两者通常使用相同的基数。
[0056]
加密的替代方案是简单地生成一系列真随机码并且将其存储在数据库中，该一系列真随机码与它们的顺序索引0、1、
……
、n、n+1、
……
相关联。然而，这不能保证它们在非常长的码序列上的唯一性。此外，检查尚未在数据库中的各个新码将在计算上是不实用的。
[0057]
相比之下，由于加密的双射性质，序列号的加密的第一个优点是其是用于以混洗顺序生成码的非常容易且常用的方法。这些码还可以被存储到数据库中(以其相关联的序列号作为索引)，就好像它们是真正随机的那样，但不需要唯一性检查。
[0058]
对序列号进行加密的第二个优点是允许我们避免使用码数据库：从码中找到序列号仅需要密钥。
[0059]
通常，用于序列化的加密使用对称加密，即，k＝k’，其应被保密。其在图3中由框e标注，具有由e-1
标注的互逆解密。对非对称密码的泛化在理论上是可能的(不同的k和k’，k保持私有)，但是以显著更长的加扰序列号为代价以确保足够的密码安全性：例如，对于rsa，推荐最少2048位，或者对于椭圆曲线密码术为256或384，等等。要求这样的长序列号(和加扰序列号)通常是用序列号来序列化物品的问题，其中需要被标记串的最短可能长度l’。
[0060]
相比之下，对称加密提供了将序列号的位长度减少到确保足够的序列号总数m的最短值的可能性。通常使用对称块加密，诸如aes、twofish、idea、des、triple-des等，用于逐一加密序列号。然而，它们使用固定的块长度：64位、128位等，因此必须应用步骤以确保更好地调整到m个所需序列号(通常短于64位)的块大小。这可以通过在这些方案(诸如feistel结构)之上应用熟知和验证的组成方法来完成。还可以从具有luby-rackoff结构的非密钥安全散列算法(如sha-2族、whirlpool等)导出ad-hoc块长度密钥密码。
[0061]
在对称加密的情况下，另一泛化包括使用非块加密，诸如流加密或流密码：输入数据的位或位组通过将这些位组与位组的伪随机序列相组合而被顺序地和连续地加密，该伪随机序列取决于密钥k而被密码地生成(通常位与原始数据位异或)。然而，应当使用重新同步机制来确保解码阶段。流加密既不相关，也不被推荐用于经由对称块加密的第一序列化方法(即，“方法1”)。与此相对，充分利用具有密文反馈的流加密并且在稍后的段落中描述第二序列化方法(即，“方法2”)。
[0062]
在标记物品之前，加扰序列号必须被格式化成l个符号的串(即，长度l或l长度码的串)，得到码，这些码因此也被加扰(因为它们在码序列内的排序是不可预测的)。格式化在图3中表示为操作“a”，并且其倒数，即，解格式化为操作“a-1”。各个符号取自n个可能的符号的有限集合，称为基数n的字母表的集合。这种格式化通常是基础转换，其中基础等于字母表基数n，可选地将码分成小的符号组，以使该转换更高效。通常，在与l长度码的开头不同的位置处的符号可以由不同的符号、从一个字母表或从不同的字母表编码，这取决于码中的该位置，并且可能具有不同的基数。然而，对于所有l个符号，通常使用相同的字母表和相同的基数。l长度码唯一地表示序列号，但通常以除了基础2(二进制)之外的另一基础，并且通常处于更适合于物品标记和人类阅读的格式。
[0063]
因此，码的长度l应足够大以允许要标记的物品的总数：l＝ceil(logn(m))，其中n是字母表基数(为简单起见，我们对于所有符号考虑相同的字母表)，logn(.)是基础n的对数，ceil(.)是最小的大于或等于-整数值，并且m是要标记的物品的不同序列号、码的总数。
[0064]
在序列化领域中，通常的做法是选择比预期物品的总数大许多倍的m以使码不易
被攻击者猜测。这降低了随机(猜测)码偶然对应于现有序列号/现有物品的概率。
[0065]
最后，为了标记物理物品，码的各个符号应当被给予图形表示。它们可以是(并且不局限于)任何人类可读字符、图形符号、表意符号、字形、绘图等，或者甚至是单色或彩色的机器可读符号，如1d或2d条形码。可替换地，人眼可能不能察觉到(例如，印有ir或uv墨水)，并且只能通过机器和算法检测。我们将准备好被标记的码的这种表示称为可标记码。
[0066]
上面已经描述了序列号在格式化成l长度码之前可以如何被加扰(即，加密)，但是这不是强制性的：还可以在序列号的加扰之前对其进行格式化。在这种情况下，我们获得由来自以上介绍的字母表的l长度符号组成的格式化序列号(但是尚未加扰，并且因此它们不是“码”)。它们的生成顺序仍是可预测的，并且然后需要加扰它们。为了在加密中保留格式化，应当使用格式保留加密(fpe)，即采用长度l的符号串作为输入、并且得到通常从具有相同基数的相同字母表中采用的加密的l长度符号串的密码。在现有技术中，fpe用于例如：对信用卡号进行加密；对一种语言的文本(诸如单词)进行加密以加密成相同语言的其他单词；等等。存在若干算法，但fpe还可以例如使用feistel结构从块密码(如上文介绍的aes、des)构造。这样的密码工作在符号级而不是位级。最后，最终获得码，必须将其转换成l长度的字形串，从而产生可标记码。使用对称块加密进行的所有先前考虑是相同的，序列号被逐一加密成可标记码。
[0067]
当码与物品同步时，这种序列化易于读取和解码：仅对码进行逐一读取和解密。然而，当发生不同步时，这种方法不再起作用：没有触发、没有可见标记、间隔等允许找到各个码的开始和结束。最糟的是，先前码的一部分可能与一个标记物品上的后续码的一部分级联。
[0068]
因此，附加的技术用于从这样的码中恢复，连同标记每个物品更多的码符号/字形，即。l’，而不是实际码长度l，以帮助该重新同步。为此目的，l长度的可标记码被连续地生成，码对应于序列号n(以及相应物品)，下一码对应于下一序列号(让我们将其标注为n+1)，下下一码对应于n+2序列号，等等。所有可标记码形成长(连续)串，该长(连续)串由以所描述的顺序级联在一起的连续l长度符号串组成。通常，为了在物品上标记码，这个长字符串在(或多或少)不受控制的位置/长度被裁剪，得到短“级联串”，即包括长度为l的码的仅一部分(长度短于l)的符号的符号串。该短级联串是在物品上有效标记的符号串。因此，短级联串是非同步的，即，不知道哪些符号/字形是这种短级联串内的标记码的第一个。我们是在不能使用其他同步技术的情况下，例如在读取码时，没有可见的标记也没有触发信号来帮助重新同步。根据本发明，为了避免这种可能的非同步效应(或不同步效应)，级联串的长度l’应严格大于l(l’》l)，因此该级联串现在包含两个连续码的至少两个部分。
[0069]
出于一般性，这还包括这样的不同步发生在读取阶段而不是标记阶段的情况，例如当存在不具有可见同步标记的长连续标记符号流时。
[0070]
根据本发明的上述方法1是一种从由上述码生成和标记处理产生的一个标记物品恢复适当码和相应序列号的方法。因此，我们具有长度l’的级联串，其中l’》l(l是码的长度)和物品内的未知同步。可以区分两种情况：l’≥(2l-1)的情况，以及l’《(2l-1)的情况
[0071]
1)情况l’≥(2l-1)：
[0072]
图1描述了具有长度l＝4的码和长度l’＝7的标记的符号串(即，级联串)的情况，因此，这里l’＝(2l-1)。人们不知道同步，即，不知道l长度码的第一符号在l’长度级联串中
的位置是什么。让我们称该位置为l长度码从l’长度级联码的开始的偏移位置，或者简称为偏移。但是人们知道，具有四个符号s
0n
、s
1n
、s
2n
、s
3n
的完整l长度码(见图1中的框(5))总是存在于l’长度级联串内至少一次，即级联块(5)+(6)，被码的不完整部分(即部分(6)(下一物品n+1的相应三个符号s
0n+1
、s
1n+1
、s
2n+1
))左和/或右包围。应当尝试l个不同的偏移位置；这是足够的，因为不同步的可能数量显然等于完整码的长度，任何附加偏移重复先前测试的偏移。
[0073]
图3所示的方法包括以下步骤：
[0074]-对于各个偏移位置(由图3上的箭头表示的当前位置1)，从l’长度级联串的开始从0到l-1，裁剪由符号s
in
(i＝0，1，2，3)组成的l长度候选码sn(5)。
[0075]-用解密密钥k’来解密该候选码，得到序列号候选n。解密是以应用加密的逆方式应用的，并且取决于此：
[0076]
(1)反转格式化(即，应用a-1
)，即，解格式化该l长度符号码候选，以获得相应的加扰序列号，然后，使用解密密钥k’来解密该结果以获得相应序列号候选n(即，应用e-1
)；
[0077]
或者：使用解密密钥k’来解密具有格式保留加密的l长度符号码(应用fpe-1
，这里未表示)以获得格式化的序列号候选，然后反转后者的格式化(即应用a-1
)以找到相应序列号候选n；
[0078]
对于该序列号候选n，计算其前一候选n-1及其下一候选n+1(2)；
[0079]-分别通过以下步骤，从该前一候选n-1和该下一候选n+1获得相应的加密且格式化的前一和下一候选(3)：
[0080]
使用加密密钥k来加密前一n-1和下一n+1序列号候选，并且格式化(经由操作a)所获得的前一和下一加扰序列号候选以分别形成前一和下一码候选s’n-1
、s’n+1
；
[0081]
或者：分别格式化(a)前一序列号候选n-1和下一序列号候选n+1以获得格式化的序列号候选，使用加密密钥k用fpe加密它们，以分别获得前一码候选s’n-1
和下一码候选s’n+1
。图5中描述了使用fpe的编码：在格式化之后而非之前应用加密。
[0082]-将前一候选s’n-1
(7)的符号与当前尝试的偏移位置之前剩余的读取级联串(6)的相应符号(如果存在)进行比较(4)(参见图3)；将下一候选s’n-1(7)的符号与刚好从当前尝试的偏移+l开始的所读取的级联串(6)的相应符号(如果存在)进行比较(4)：
[0083]
如果所有符号匹配(来自4的结果m，左侧和右侧)，则找到正确的偏移、正确的码和正确的序列号n：可以保留这个序列号n作为正确解码的候选；
[0084]
如果至少一个符号比较失败(即，失配，结果mm，左侧或右侧)，则没有序列号对应于该偏移；
[0085]
如果已尝试从0到l-1的所有偏移，并且对于所有情况，至少一个比较的符号对失配(mm)，则不能对码进行解码：所读取的码可能具有错误。
[0086]
通常，人们期望级联串中仅一个尝试的偏移得到有效的解码序列号n。然而，有时可能从同一l’长度级联串成功地解码多于一个的序列号n’和n”：这是可能不能避免的模糊性：对于任何有效码，在m个码的完整序列中可能存在当不同步时匹配的另一码。然而，在这种情况下，n’、n”中仅有一个是正确的序列号，即已经用于编码。为了减少这种模糊性，可以应用以下技术：
[0087]-确保l足够大，使得所使用的字母表具有足够的基数n；实际上，测试示出对于l＝
6长度码，使用base 32crockford编码(即，字母表基数n＝32)，对于l’＝2l-1＝11，以1.7x10-7
的概率出现模糊性，并且对于l’＝2l＝12，以6.2x10-9
的概率出现模糊性；
[0088]-利用先验已知信息，该先验已知信息不被编码在码本身中，但通常与相应的批量物品相关，从该先验已知信息中，序列号序列的预期特性可以是已知的。示例可以是预期的批号，即，起始n1序列号和结尾n2序列号，因此可以拒绝不遵守条件n1≤n≤n2的任何经解码的n。
[0089]
原则上，l’不具有上限，并且增加l’减少了以上模糊性的发生。但是当然，l’被选择为在目标背景下如实际可接受的那样小。
[0090]
2)情况l’《2l-1：
[0091]
这种情况在图2中描述，其中l＝4并且l’＝6，因此l’《2l-1。在这种情况下，对于一些偏移位置，存在完整的l长度码(5)，但是对于一些其他偏移，在l’长度级联串内不存在完整的码：对于这些后者，级联串由来自两个连续码的部分(6)的级联组成，但是它们都不是完整的。然而，由于l’》l，因此完整码候选仍可针对一些偏移进行裁剪。
[0092]
解码处理与上面情况l’≥2l-1的情况相同，在从级联串中裁剪完整的l长度码候选时，不需要进行修改。但是，如图4所示，在长度《l的码候选的情况下，需要特定的方法。在这种情形下，如下所述，当l’《(2l-2)时，定义起始偏移位置p为负。另外的技术用于仅存在两个不完整的候选码部分的偏移。这是当p为负(p＜0：符号在左侧缺失)时或者当候选码的最后符号的位置超过级联串长度(即，p+l》l’：符号在右侧缺失)时的情况。
[0093]
不完整码候选情况通过对该(这些)缺失符号的穷尽搜索来解决。解决不完整码候选情况工作如下：
[0094]
尝试的第一(最左)偏移位置可以由以下给出：p＝floor((l
’‑
(2l-1))/2)，相对于l’长度级联串的开始，floor(.)最大小于或等于-整数值，并且“/”除法；|p|实际上是相对于长度(2l-1)的潜在最大缺失符号的一半。目标是最小化候选码的左或右缺失的符号，这是为什么p可以是负的；
[0095]
最后偏移位置是p’＝p+l-1；让我们还定义该最后偏移的最后符号的位置为q＝p’+l-1＝(p+l-1)+l-1＝p+2(l-1)，q为候选码的最后符号在长度l’的级联串内的最右位置；
[0096]
对于从p到p’(包括p’)的各个偏移位置p，裁剪l长度码候选。我们具有以下子情况：
[0097]
如果p≥0并且p+l-1《l’，则在l长度候选码的左侧或右侧没有缺失符号：是完整的，并且不再需要做什么；
[0098]
如果p《0(如果p《0可能)，在左侧具有|p|个缺失符号；因此，r＝|p|是l长度候选码左侧的最大缺失符号。另一方面，如果p+l》l’，则在右侧具有缺失的符号；因此，在l长度候选的右侧最多r＝q-(l
’‑
1)＝p+2(l-1)-(l
’‑
1)＝p+2l-l
’‑
1个缺失的符号。在这两种情形下，左侧或右侧的缺失符号填充有来自它们的字母表(ai，i＝0，...，n-1)的缺失符号的所有组合(8)(参见图4)，从而产生同样多的l长度码候选(5)。注意，作为条件l’》l的结果，符号可以在左侧或右侧缺失，但从不在这两侧缺失。
[0099]
对于各个这种候选l长度码，后续步骤与针对上述情况l’≥2l-1的这些步骤完全相同。唯一的区别在于，对于各个缺失符号的情况，根据缺失符号的穷尽搜索，一个候选在这里变成许多候选。
[0100]
为了减少模糊性，对于情况l’》＝2l-1，可以使用批量相关的先验已知信息：预期的批量范围，即起始n1和结尾n2序列号等。
[0101]
在上述方法1中：
[0102]-缺失的符号穷尽搜索可能在计算上是繁重的，在实践中限制该方法在实际场景中可以实现的缺失符号的最大数量。因此，l’应保持合理地接近2l-1：给定偏移位置所需的穷尽搜索的最大数量为nr，其中r是来自基数n的字母表的缺失符号的最大数量，并且该数量迅速增加。例如，可以认为r＝2或3个缺失符号的最大值是32基数字母表的可接受的最大值(即，对于n＝32，r＝2引起1024次迭代，并且r＝3引起32768次迭代！)。
[0103]-如已经提到的，起始偏移位置p是负的，以限制缺失符号的最大数量r，否则，如果偏移位置简单地从0开始，则这个数量将是两倍多。
[0104]-最后，猜测缺失符号增加了在解码阶段可能发生的模糊性的出现，因为当l’减小时，在l’长度级联串中可获得更少的信息。在极端情况l’＝l中，所有尝试的偏移位置都将是模糊的的，这就是约束l’》l已被固定的原因。再次，l’应保持合理地接近2l-1以实现低模糊概率。
[0105]
与序列号被逐一加密和解密的方法2相比，根据本发明的上述方法1依赖于块加密方法。然而，存在可用于解决不同步问题的具有自重新同步能力的密码。这些被称为自同步流密码，并且这样的属性使得它们自然地适合于不同步序列化。
[0106]
流密码是加密方案，其中，明文数位(或字符、符号等)与密钥相关的伪随机流组合。各个明文数位与伪随机流的相应数位逐一加密，产生加密数位。由于各个数位的加密取决于密码的当前状态，因此也被称为状态密码。通常，数位是位，并且组合运算是异或(xor)。为了实现逐符号(非位)加密，使用格式保留加密(fpe)，保留各个符号的字母表。由于其也是流加密，因此将其命名为流fpe或sfpe。
[0107]
自同步流密码是当前状态取决于密文的k个先前数位、字符等的流密码。这种方案也被称为异步流密码。自同步的想法具有以下优点：接收器在接收k个密文数位之后自动地与密钥流生成器同步：在错误的情况下，该方案在解密k个数位之后自动地重新同步。自同步流密码的示例是在密码反馈(cfb)模式中使用的块密码。
[0108]
流密码经常因其速度和简单性而被使用，且尤其在明文以未知长度的量出现的应用中。这还避免了当数据应被连续地逐数位地(通常：字符、字节)传输时需要对块密码进行填补的问题(以及所导致的性能或空间的损失)
[0109]
通用流密码的示例是：chacha、rc4、a5/1、a5/2、chameleon、fish、helix、isaac、mugi、panama、phelix、pike、seal、sober、sober-128和wake。也可以从具有特定结构的块密码或加密安全散列码来构造安全流密码。
[0110]
与方法1相同的考虑因素代表加密密钥k和解密密钥k’：理论上，流加密可以是对称加密或非对称加密。
[0111]
然而，现有的流和fpe实际上是对称密码。这是由于它们的逐符号性质，符号是短位长度元素，而如rsa的非对称加密将需要大(或非常大)的字，这是不实际的。最重要的是，用于加密的伪随机序列需要相同地重新生成同一种子，意味着具有k’＝k的对称密钥。
[0112]
虽然流加密/解密自动重新同步，但没有给出关于l长度码的实际开始的信息。结果，需要附加的技术来识别级联串内的码同步，这将在下面描述。
[0113]
如图6所示，为了生成序列号和标记，本发明使用应用于格式化序列号的自同步流密码。如在方法1的情况下，序列号以连续的方式(标注为0、1、2、3、4、
……
、n-1、n、n+1、
……
、m-1)与物品唯一地相关联。然而，与方法1不同，它们优选首先被格式化，被级联为连续流，然后被加密。因此，需要sfpe(“流fpe”)。
[0114]
通过用于加密的图6以及用于解密的图7来说明该方法，该方法应用于码长度l＝4、所接收的加密符号的数量l’＝7、并且因此k＝l
’‑
l＝3的序列化。单向加密函数f从k个先前加密的符号s
in
(i＝0，1，2
……
)和密钥k连续地生成伪随机值，在箭头的方向上前进。出于一般性，伪随机流值与明文数据符号c
in
的组合被表示为用于加密的加法“+”(例如，在图6中，加至c
3n
)，并且被表示为用于解密的减法
“‑”
(例如，在图7中，从s
1n
中减)。在解密中，前k个符号不能被解密，因为这些符号在l’长度的级联串中缺少前k个符号，并且在图7中被标注为“？”。
[0115]
将l’＝l+k(其中k》0)定义为能够解密至少l个符号的(符号串的)最小长度。但通常l’≥l+k，或l’＝l+ t+k，其中t≥0。在用于加密的图8中以及用于解密的图9中描述了整体方法，其中，l＝4、t＝1、k＝3并且因此l’＝8。
[0116]
与方法2对应的码的生成工作如下：
[0117]-如方法1中所定义，使用来自字母表的码符号格式化序列号，得到图8的格式化序列号c
in
。它们还没有被加扰。
[0118]-格式化的序列号可以视为被级联，以与输入序列号相同的顺序布置，以形成较长的且尚未加密的连续串。级联串的长度是l’＝l+t+k，其中k》0的是反馈长度，并且t≥0的是当序列号必须被解码时有助于重新同步的额外符号的数量。
[0119]-然后，使用加密密钥k将自同步流密码应用到这个未加密的串上，将串符号c
in
逐一连续地取作输入并且将由k(其中k》0)个先前加密符号形成的序列作为反馈以在解密时实现自同步。反馈跨连续码传播，意味着各个码的第一符号中的一个或多于一个取决于来自前一码的加密符号的反馈。
[0120]-为了在符号内工作，该密码是流格式保留加密(sfpe)，因此，逐符号地将格式化的序列号从一个(多个)字母表加密成一个(多个)字母表(通常是相同的字母表)，从而产生加密的符号s
in
。这产生以连续顺序加密且级联的l长度码的“无尽”串。加密一个符号可以例如通过将加密函数的输出与输入符号算术相加、将相应字母表的基数模n来工作。
[0121]-对于方法1，以(或多或少)不受控制的方式将这个串切割成l’长度的子串，其中，l’》l，形成级联串。应当确保l’＝l+t+k，其中k》0且t≥0，以强制执行由密文反馈机制产生的未来可解码性。
[0122]-如在方法1中转换成字形或图形元素以形成可标记码mc的这些l’长度级联串的符号随后被应用到连续物品上。
[0123]
级联串应至少长度为l’＝l+k(其中t＝0)，以确保对至少l个符号进行适当解码。在解密之后，这些符号可以与同当前码级联的先前码的一部分不连续。然后，如在方法1中，在知道先前码相对于当前码n是n-1的情况下，将使用接下来描述的重新同步技术。另外，使用额外符号(其中t》0)提供附加信息以帮助重新同步，已知流密码确保(l+t)个符号被适当解密(但不指示实际码偏移)，如下文描述。
[0124]
在与从0至m-1的序列号相对应的连续不间断且唯一的码序列的假设中，各个码取
决于其前一码。在不同批量物品生成的码的情况下：各个批量的前l’长度的级联串将必须包括前一批量的最后码的k长度结尾部分；所有批量都必须连续生成，以知道各个批量的最后码；并且最前面的级联串(对应于序列号0)将需要初始k长度反馈串，其被定义为随机的，或者为了简单起见被设置为固定常数，例如“全零”。
[0125]
除了加密密钥k之外，与从0至m-1的序列号相对应的整个码序列将完全取决于这个初始反馈串。这个值是将来解密所需要的，但是根据定义它被包括在级联串中。影响后续加密流的这种初始化值通常被称为密码社区中的随机数或初始化向量(“iv”)。
[0126]
然而，强制完整码序列为唯一的(如刚才所解释的)对于序列化不是必需的。在实践中，码可以由不同批量生成，这些批量不必是连续的，从加密反馈的观点来看在彼此内也不一致。不同批量的唯一所需约束是对应于序列号相对于彼此的非重叠范围。可以在各个批量的开始时定义iv任意值(或固定常数或“全零”值)。在极端情况下，尽管不实用，但可以针对各个新码生成随机iv。恰好可以跳过第一码(或前几个码)以生成一批量的第一级联串。这是可能的，因为iv/反馈符号被包括在级联串内并且因此不需要存储用于解密：来自级联串的该解密总是得到正确的序列号n。
[0127]
但只有在相同批量必须同样地重新生成若干次的情况下，才必须存储用于批量的iv(批量具有开始和结束)，除非使用常数(例如“全零”)iv。此外，这种批量附接的iv可以用作附加信息(或“辅助信息”)以检查解码的级联串实际上被正确解密。
[0128]
在解码阶段，自同步流密码确保总是正确地解密来自前k个符号之后的任何输入的符号，但是自身不给出同步信息：仍然必须找到至少一个码的开始(和结束)。因此，需要附加的方法来找到码在级联串内的偏移位置。
[0129]
第一种方法是提供附加的符号(t》0)，以允许通过逐符号的比较来验证尝试的偏移位置。这对应于以下“序列号解码”描述的解码阶段情况1，其中，在l长度加密编码中不包括同步信息。然后，t》0简单地添加更正确解码的符号，有助于减少解码模糊性。
[0130]
第二种方法是在格式化序列号时将附加同步信息(在加密之前添加)，称为同步标记，作为l长度码的一部分(添加的信息现在被加密)。以下是“序列号解码”描述的情况2。这可以但不限于通过以下来实现：
[0131]-类型1的标签：除了格式化的序列号的(l-1)个剩余符号之外，例如在各个格式化的序列号的开始处添加同步符号。
[0132]-类型2的标签：将来自字母表的一个子集的符号用于各个格式化的序列号的第一个符号(通常为字母表的一半)，并且将来自另一字母表子集的符号用于(l-1)个剩余符号(通常为互补的一半子集)。
[0133]
重要的是，在非加密域中完成这种同步标签，使其隐藏在所得到的加密码和级联串中：不向攻击者给出关于同步的信息，攻击者知道其仅访问加扰码。为了实现这一点，在字母表的完整基数n上加密符号，而不管用于输入符号的不同字母表子集，或者是否使用定界符符号。结果，这样的标签不等同于引入分隔码的可见标记。
[0134]
该标签在解码阶段应该是可逆的，以允许从解密的格式化序列号恢复原始序列号n。除了基础转换之外，可以将标签视为仅格式化序列号时的附加步骤。
[0135]
由于标签添加不是原始序列号信息的一部分的用于同步的信息，因此标签可以增加所需的码长度l以用给定字母表相对于没有标签的版本覆盖所有m个物品。根据上述两个
标签示例，对于总共m个序列号和基数n的字母表，获得以下码长度l值：
[0136]
类型1的标签：插入定界符符号：
[0137]
l＝ceil(logn(m))+1，
[0138]
类型2的标签：使用各个基数n/2(假设n是偶数)的两个不同的字母表子集，一个用于第一符号，并且另一个用于剩余符号：
[0139]
l＝ceil(log
n/2
(m))
[0140]
实际上，l的增加通常为1或2：例如，对于32个不同符号的字母表(称为基数的值)：
[0141]
对于m＝106个物品：在没有标签的情况下l＝4，对于类型1的标签l＝6，并且对于类型2的标签l＝5，将选择后者以针对物品标记将l最小化。
[0142]
对于m＝10
11
：在没有标签的情况下l＝8，在类型1的标签的情况下为9，在类型2的标签的情况下为10，那么类型1是优选的。
[0143]
对于基数40的字母表：
[0144]
对于m＝10
11
：在没有标签的情况下l＝7，在类型1的标签的情况下为8，在类型2的标签的情况下为9，因此类型1的标签是最好的。
[0145]
关于方法1，码的各个符号在标记物理物品(诸如任何人类可读字符、图形符号或如条形码的机器可读符号)之前应以单色或彩色被给予图形表示。
[0146]
关于序列号解码方面，在图9中描绘了根据方法2的序列号解码。对于方法1，可以从自物品读取的l’长度的级联串中解码实际序列号。但是与方法1不同，解密总是输出正确解码的符号，但是仅在经处理的l’长度的级联串中的前k个符号之后。
[0147]
因此，仅从位置k直到级联串的最后位置(l
’‑
1)的符号可以被准确地解密。在解密之后忽略前k个未解密符号(在图中标注为“？”)，得到正确解密的符号的长度(l
’‑
k)串。因此，通常，获得正确解密的符号的长度(l
’‑
k)＝(l+t)的串，其中，t≥0是额外符号的数量。然而，这些符号仍然可能是不同步的。人们还不知道正确的同步，即，l长度码在该解密的级联串内的实际偏移位置。因此，在解密之后需要进一步的同步技术。
[0148]
级联串的解密如下进行：
[0149]-使用sfpe解密密钥k’对l
”‑
长度级联串进行解密，得到(l
’‑
k)或(l+t)长度解密的级联串。因而，关于所描述的加密阶段，可以通过从输入符号减去加密函数的输出对相应字母表的基数n取模来解密符号。该处理工作如下：
[0150]
从偏移位置k并且优选地到偏移(l
’‑
1)以利用t个额外符号(如果存在)、或者至少到偏移(l+k-1)来顺序地解密各个级联串符号。对于各个符号解密，加密级联串的前k个符号用于反馈；
[0151]
从0至(k-1)的偏移的符号(用“？”表示)不能被解密，因为反馈的加密符号不可用于它们：因此，在所得到的(l
’‑
k)长度的解密级联串中忽略它们。
[0152]
所得到的(l
’‑
k)长度串是长度为(l+t)的准确解码的符号串，其中，t≥0。其包含完整的l长度格式化的序列号，或连续格式化的序列号的两个可能不完整的部分。
[0153]
应当确定同步以重建原始序列号，即，应当找到解密的级联串内的两个码部分之间的边界。可以区分以下两种情况：情况1，其中不存在附加的同步标签；情况2，其中存在同步标签。并且对于这两种情况，t＝0，或者t》0，提醒：
[0154]-级联具有长度：l’＝(l+t+k)，其中t≥0并且k》0；
[0155]-解密的级联串具有长度：(l
’‑
k)＝(l+t)并且可以是不同步的。
[0156]
相应地，同步步骤包括：
[0157]
情况1：不存在同步标签：
[0158]-子情况1.a：对于l长度解密的同步串(即，t＝0，或者仅保留前l个正确解码的符号)：遗憾地提取从0至(l-1)的偏移位置开始的l长度格式化的序列号候选，导致同样多的模糊性！这是因为任何偏移移位的格式化序列号候选n在由m个可能的序列号形成的空间中的其他地方等于某个有效的0偏移移位的格式化序列号n’。并且没有标签意味着没有同步信息可用于指示实际码偏移。因此，该子情况1.a不适用于该情况1并且必须被丢弃。
[0159]-子情况1.b：具有严格超过l个正确符号的(l+1)长度至(2l-1)长度解密的同步串(即，0《t《l)是可用的。为了证实，可以利用剩余符号来验证各个偏移移位的l长度格式化序列号候选。类似于方法1，这通过以格式化形式逐符号地匹配从n计算的n-1和n+1来完成，但是区别在于不需要解密/加密(符号已经被解密)。这与方法1的l＜l’≤(2l-1)的情况类似。对于一些偏移位置，可能依然出现模糊性，但是随着t增大，模糊性的出现减少：然后，长度l’的级联串应合理地接近(2l+k)(或者t合理地接近l)，以实现模糊性的实际上低概率。
[0160]-子情况1.c：(2l+k)长度级联串，或2l长度解密级联串，或更长，是可用的，这暗示t≥l：可以如上所述验证各个偏移移位的l长度格式化序列号。这与方法1的l’》2l-1的情况类似。然而，在该子情况下，可以消除模糊性，因为一个且仅一个有效候选n与对(n-1，n)或对(n，n+1)一致：这可以被检查，因为一个具有2l有效符号。此外，利用多于2l的正确解密的符号，甚至可能通过检查具有更多出现的序列号(如(n-2)、(n+2)等)的解码的符号来检测输入级联串是否具有错误。
[0161]
情况2：存在同步标签：
[0162]
一旦解密，各个(l
’‑
k)或(l+t)长度正确解密的级联串包含用于加密的标签。从描述编码时给出的类型1和类型2的标签的非穷尽示例，解密的标签包括：
[0163]
类型1的标签：在各个格式化序列号的开始处插入的定界符符号。
[0164]
类型2的标签：来自字母表子集之一的符号指示其是格式化的序列号的第一个符号，其他符号来自互补的字母表子集。
[0165]
然后可以从标签推导出正确的偏移位置。此外，有可能：
[0166]-首先证实标签的一致性以检测错误的输入，并且在错误的情况下拒绝解码。例如，通过检查：
[0167]
定界符符号被精确地l个位置分隔；
[0168]
第一个符号由精确的l个位置分隔；
[0169]-然后，重新同步解密的级联串，去除标签，并且重新形成适当的序列号n。
[0170]
考虑如以上情况1中的子情况，具有：
[0171]-子情况2.a：l长度的解密级联串可用(或者t＝0)：重新同步，去除标签，并且在知道期望的序列号序列是(n-1)、n、(n+1)的情况下重新形成序列号n。
[0172]-子情况2.b：l’＝(l+t+k)，其中，t》0：由于标签，所以重新同步，并且额外的符号可以用于匹配所得到的符号，以确保序列号n可以被正确解码，已知预期的序列是(n-1)、n、(n+1)。通过更多的额外符号t，甚至可能检查更多的符号，在检查中可能包括(n-2)、(n+2)或更多。因此，如以上情形1、子情形1.c那样，检测输入级联串是否错误并且拒绝解码变得
更容易。
[0173]
对于子情况2.b，由于解密的级联串的比较不是直接用二进制序列号n(虽然这不排除)而是在格式化域中更容易进行，这可以如下进行：
[0174]
使用相应的基础(符号ci)在格式化的域中进行计算，而不是在序列号域(n)中计算，但如果存在则去除同步标签；
[0175]
解密后的级联串的前一部分和后一部分必须按照正确的顺序重新级联，由于前一个对应于序列号n-1并且当前为n，因此前一个加1，或者由于是n+1，因此下一序列号减1，以恢复出适当的l长度未加密码；由于sfpe输出正确解密的值的能力，因此已知该重构的格式化序列号是正确的；
[0176]
最后，该重构的格式化序列号可以是未格式化的以获得实际序列号n。
[0177]
对于以上两个子情况，仍可以使用辅助信息来减少模糊性，例如：
[0178]
针对解码的n，检查预期的批量范围：开始n1和结尾n2个序列号，检查n使得n1≤n≤n2。
[0179]
如上面对初始化向量的讨论中所解释的，所存储的初始化向量(iv)和针对各个批量所存储的所得中间码值。
[0180]
关于反馈长度k：
[0181]
反馈长度k可以较小，使得k≤l。然而，应该合理地足够大，即接近l，尤其是如果l较小时。反馈长度k用字母表基数n定义对于给定的加密密钥k的加密的可变性v(即，可能的不同加密的数量)：v＝nk。
[0182]
攻击者应该不能容易地猜出有效的反馈串。另一方面，对于k不存在上限，但是可能显著大于l的k值不会带来如此多的附加安全性。提出可变性v应为至少数百万以实现良好安全性，从而限制用于攻击序列化的强力方法的有效性。
[0183]
例如，对于32的字母表基数，对于诸如6等的l的小值，可以提出k＝l或(l-1)，并且对于较大的l值，k被固定为6。对于字母表基数n＝32，k＝4确保加密的可变性v＝1百万，并且k＝6实现v＝10亿。
[0184]
本发明主要以人类可读序列化为目标，其中用户潜在地手动地键入和查询码。然而，在本文档中所描述的技术不仅限于人类可读编码且还可以解决机器可读编码。编码可以包括：
[0185]-人类可读编码，使用拉丁字母表、西里尔字母表、亚洲字母表或任何其他字母表；
[0186]-人类可读编码，但针对机器读取使用特殊策略和字体(如(但不限于)用于光学字符识别的ocra)进行优化；
[0187]-可以线性印刷的仅机器可读码，例如(但不限于)：
[0188]
非常小的1d/2d条形码的序列；
[0189]
用于邮政应用的智能邮件条形码(im)或类似物；
[0190]
由小图形元素构成的专有编码，各个图形元素表示字母表符号并且被线性印刷。
[0191]
图10示出了由线性印刷的迷你1d/2d图案构成的专有条形码/符号系统的示例，各个图案表示字母表的符号。
[0192]
标记可以以下形式实现：
[0193]-使用连续喷墨、激光雕刻或允许直接编码的任何其他技术的直接编码；
[0194]-对带进行预编码，所述带可以稍后被切割并粘贴在物品上，而不保证配准。
[0195]
根据本发明的序列化可以应用于由于各种原因(诸如移动物品的高速、没有复杂的配准机制或配准的机械不可能性)而难以配准的每种情形。如图11上所示，结合在纸币中的安全线9是可以使用这种序列化的良好示例。本发明中公开的序列化方法将可靠地标记这种线10，而不管其失准如何，如图12中所示，并且甚至可以用于机器读取。该方法允许减少(至零)解密错误的概率，实现适当的认证/识别。该方法适合于可以被线性地布置为连续串的任何编码或标记。
[0196]
以上公开的主题将被认为是说明性的而非限制性的，并且用于提供对由独立权利要求限定的本发明的更好理解。