一种基于西格摩德函数的沥青混合料主曲线的构建方法与流程

本发明涉及一种基于西格摩德函数的沥青混合料主曲线的构建方法，属于道路工程领域。
背景技术：
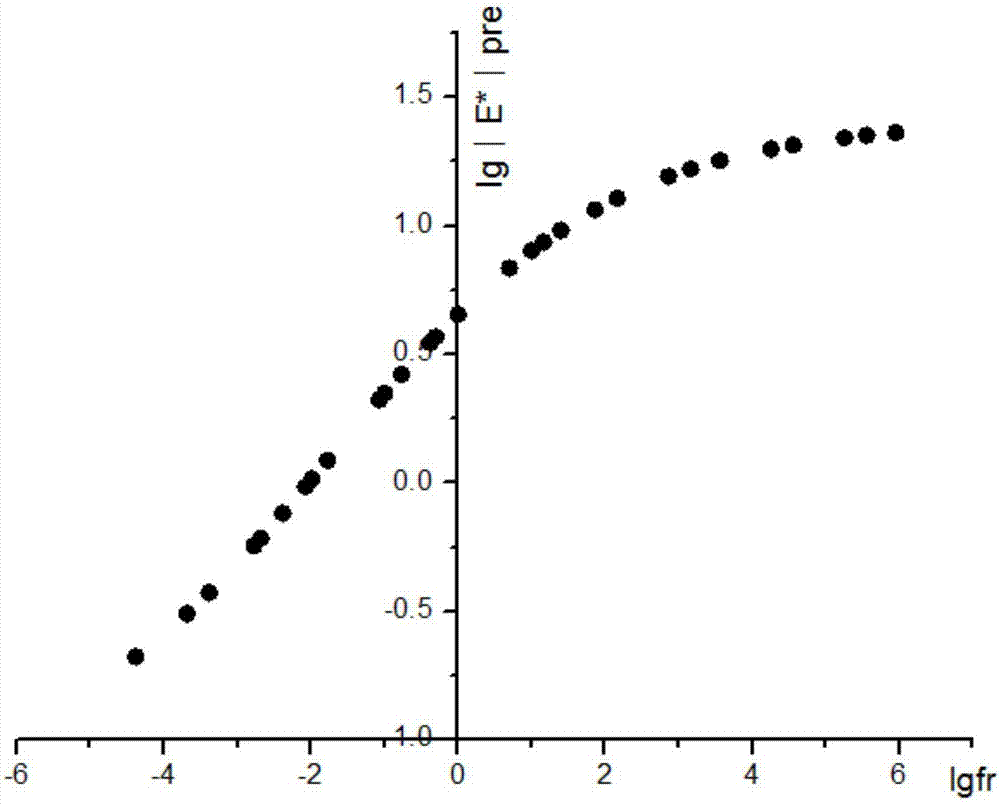
：沥青混合料材料在三维空间中的力学行为是多种多样的，但根据粘弹性材料的研究，可以认为这些力学行为具有相当明确的规律性。这种规律性不仅表现在材料应力-应变相应关系分别依赖于温度效应与时间性，也表现在材料力学行为中时间效应与温度效应的等效性及相互转换关系上。利用这样的时间温度等效转换，我们可以将一定时间范围、温度范围内的试验测定结果推延到更加广泛的时间温度空间中去。这将大大减少材料研究的试验工作量，并在相当程度上降低对试验装置的技术要求。现有的wlf公式法，得到玻璃态转移点tg的值，但是玻璃态转移点的物理结果依赖于温度，降温速度不同，材料自由体积的热膨胀规律也不同。缓慢、间断的改变温度，将得到与快速连续降温使测定结果不同的玻璃态转移点tg，因此，其测量过程非常复杂，精确值也难以控制。尽管依赖于经验公式的wlf法，虽然无需测定玻璃态转移点tg的值，但是其以某一假定，反算出实验结果的温度ts作为基准温度，其结果的准确性并不总能满足目标。本发明方法借助于excel的规划求解的功能，其方便性和准确性将得到很大程度的提升。技术实现要素：为了避免上述现有技术所存在的不足之处，本发明旨在提供一种基于西格摩德函数的沥青混合料主曲线的构建方法，不但使沥青混合料研究的试验工作量大大减少，也显著提高了数据的准确性。本发明基于西格摩德函数的沥青混合料主曲线构建方法，包括如下步骤：步骤1：将不同测试温度t、不同加载频率f下所测得的动态模量值|e*|输入至excel软件中，并换算成以10为底数的对数形式得到lg|e*|test和lgf；所述测试温度t至少设置为五个，每个测试温度t下至少设置6个不同的加载频率。步骤2：在绘图软件origin中以lgf为横坐标、lg|e*|test为纵坐标作图，得到不同温度下的动态模量-频率的散点曲线图；步骤3：选定某一个温度值作为参考温度，在动态模量-频率的散点曲线图中获得其它温度下的曲线到参考温度下的曲线的水平距离lgat，将lgat记为移位因子，并记录至excel表中；步骤4：在excel表中计算出各个测试温度下的缩减频率fr及其对应的缩减频率对数lgfr，其中lgfr＝lgat+lgf；步骤5：在excel中取测试温度下lg|e*|test的最小值为西格摩德函数的未知参数δ的近似值，以lg|e*|test的最大值减去最小值记为西格摩德函数的未知参数α的近似值；然后在参考温度下的动态模量-频率的曲线上取任意两点，联立方程组，得到剩下的两个未知参数β和γ的近似值；所述西格摩德函数为：步骤6：根据已取得的未知参数α、β、γ、δ的近似值，基于西格摩德函数求得不同lgfr下的动态模量的预测值lg|e*|pre；以预测值和实验值之差的平方作为误差值，以所有误差值之和作为总误差；步骤7：采用excel的规划求解功能，以总误差的最小值作为目标单元格，选取各个移位因子lgat和四个参数δ、α、γ和β作为可变单元格，进行非线性规划求解，再根据非线性规划求解后所得移位因子lgat和四个参数δ、α、γ和β的数据获得调整后的lg|e*|pre；步骤8：以非线性规划调整后的动态模量预测值的对数值lg|e*|pre和缩减频率的对数值lgfr作图，即为所需要的沥青混合料主曲线图。通过沥青混合料主曲线图，可以得知实验所没有测得的动态模量值，更可以预测实验无法测得的动态模量值，这对沥青混合料的变形预估研究具有重大的意义。由西格摩德函数公式可知，当lgfr趋于负无穷大时，动态模量对数值lg|e*|最小值等于δ，因此δ初始近似值可取原始数据中最小的动态模量值；当lgfr趋于正无穷大时，动态模量对数值lg|e*|最大值等于δ+α，因此α的初始近似值可取为原始数据的动态模量对数值的最大值与最小值的差。本发明的有益效果体现在：本发明借助于excel自带的数据处理和拟合功能，其操作更加简便易行，由于借助计算机运算，避免了复杂的人工计算，其准确度也得到极大提高。附图说明图1是实施例中，以lgf为横坐标、lg∣e*∣test为纵坐标作图，得到对应的动态模量-频率曲线图。图2是实施例中，以动态模量预测值的对数值lg∣e*∣pre和缩减频率的对数值lgfr作图得到的沥青混合料主曲线图。具体实施方式下面将结合具体实施例对本发明做出进一步详细的说明。1、将5种不同温度以及每种温度下六个加载频率以及相应的动态模量值记录至excel中并换算成以10为底数的对数形式，见下表1：表12、在origin中以lgf为横坐标、lg∣e*∣test为纵坐标作图，得到对应的动态模量-频率曲线图，见图1。3、选取21.1℃为参照温度，其它曲线到该曲线的水平距离为lgat，lgat见下表2所示：表2lgat(-12.2℃)4.47359lgat(4.4℃)2.22874lgat(21.1℃)0lgat(37.8℃)-1.74549lgat(54.4℃)-3.328614、根据lgfr＝lgat+lgf，得到各个温度下的缩减频率对数，见下表3：表35、以测试温度下所得原始数据lg∣e*∣test中的最小值近似为δ，最大值与最小值的差近似为α，然后在21.1℃对应的曲线上任取两点，这里我们取得是0和1及其所对应的动态模量对数值，联立方程组得到结果β和γ，如下表4所示：表4δ-0.648937107α2.026822902γ-1.5060476β0.7612193496、根据西格摩德函数和已求得的未知参数值，计算出不同lgfr下动态模量对数的预测值lg∣e*∣pre，以预测值和实验值之差的平方作为误差值，以所有误差值之和作为总误差用以衡量构建方法的准确性，总误差越小表明本发明构建方法越准确。下表5是未进行规划求解时的动态模量对数值的预测值和其误差，其中误差＝(lg∣e*∣pre-lg∣e*∣test)^2,总误差为所有的误差值之和。表5lgfrlg∣e*∣pre误差总误差5.9547946641.3773331463.05421e-075.6720496475.5568546561.3768797160.0003264285.255824661.3763030810.000831894.5568546561.37335740.0036907174.255824661.3707690380.0055015193.5568546561.3576266580.0118293263.5612320691.3577584570.0100406443.163292061.3415327870.0153398862.8622620641.3212632640.0182789772.163292061.2236796080.0147866691.8622620641.1453740980.0073444411.163292060.8290967380.0140035621.3979400090.9586795011.24387e-0610.7253516980.0267924620.6989700040.5111234940.1004589110-0.0036340070.446763478-0.301029996-0.1850159520.571069976-1-0.4586783820.679762963-0.375472549-0.2239003190.607421557-0.773412558-0.3911409160.691259431-1.074442553-0.4771464890.662485038-1.773412558-0.5854807230.451043118-2.074442553-0.6081459530.316943222-2.773412558-0.6345119810.144576925-1.98587966-0.6024591720.396938932-2.383819669-0.6231454090.252953663-2.684849664-0.6324704680.164495718-3.383819669-0.6431596860.041830189-3.684849664-0.6452618190.015276809-4.383819669-0.6476529141.64915e-067、采用excel的规划求解功能，以总误差的最小值作为目标单元格，选取各个移位因子和四个参数δ、α、γ和β值作为可变单元格，进行非线性规划求解，得到结果见下表6：表6根据非线性规划求解后所得移位因子和四个参数δ、α、γ和β值获得的lg∣e*∣pre及误差数据见下表7。表7由表5和表7数据可知，通过规划求解得到的最终结果，其总误差相比于先前总误差大大的减少，这表明所得到的最终动态模量预测数据与原始实验数据相差无几，极大地提高了准确性，这更加有利于沥青混合料后续的实验研究。8、最后以动态模量预测值的对数值lg∣e*∣pre和缩减频率的对数值lgfr作图，即为所需要的沥青混合料主曲线图，见图2。通过图2主曲线，可以得知实验所没有测得的动态模量值，更可以预测实验无法测得的动态模量值，这对沥青混合料的变形预估研究具有重大的意义。当前第1页12