一种球形贮箱微重力环境下液体晃动的建模方法与流程

本发明应用于充液航天器液体晃动分析领域，具体来说是一种球形贮箱微重力环境下液体晃动的建模方法。

背景技术：

根据航天器飞行过程中所受过载的情况，贮箱中流体的运动可分为失重、微重、低重、常重和超重数种工况，对于自旋充液航天器，还有快旋和慢旋工况等。对于充液航天器，主要研究失重或微重以及低重工况和自旋工况的流体运动特性。理论和实践表明，当bond数(其中ρ是液体的密度；g为过载加速度；l0为特征长度，一般取为自由液面的半径；σ为表面张力系数)为0时，可视为失重工况；当bond数介于0到100之间时，可视为微重工况，当bond数大于100时，可视为低重工况甚至常重工况研究其运动特性的影响，这时可忽略表面张力的影响。

贮箱晃动液体晃动问题的研究方法可分为理论研究、数值研究、实验研究等三类。在理论研究方面，20世纪60年代，abramson首先应用不可压缩、无粘、无旋的线性势流理论建模，将流体动力学方程演绎为速度势的拉普拉斯方程，具有线性化的边界条件，采用分离变量法可以得到了速度势特征函数和特征频率的解析解。实际上，只有少数几种形状的容器，可使用分离变形量法对上述拉普拉斯方程的边值问题进行解析求解。对于一般形状容器，由于壁面几何结构的复杂性，很难直接用解析方法求解，需要进一步结合数值方法进行分析求解。数值研究的方法依据所采用的理论模型的不同，主要可分为两类：一类是基于势流理论得到时空分离的动力学方程，从而通过特征值分析实现频域解耦的研究方法。另一类则直接从navier-stokes方程出发，对液体晃动进行时域的数值仿真，通常称为cfd(计算流体动力学)方法。无论是理论研究，还是数值研究，它们结果的正确性常需要通过实验来检验。

目前，低重环境下充液贮箱小幅线性晃动的动力学特性研究比较成熟，其理论模型广泛应用于航天器的工程设计。但随着航天器的发展，高定位精度航天器贮箱内的液体晃动面临新问题。航天器具有较高的定位精度，在姿态机动稳定过程中，使得航天器贮箱面临微重力学环境，贮箱内推进剂的表面张力开始显现，可能导致贮箱内推进剂的晃动呈现复杂晃动特性，对平台高精度姿态控制产生影响。目前已有的小幅线性晃动建模方法已然不能满足其动力学特性预测的需求。

微重环境小幅液体晃动问题目前基本采用基于计算流体力学的商业软件进行求解，获得力和力矩的时域曲线，但该方法一方面直接用于控制系统设计较为困难，另一方面求解效率较低，求解耗时较长，难以满足工程需要。因此，有必要开发一种高效的适用于工程应用的微重小幅液体晃动建模方法。

技术实现要素：

本发明解决的技术问题是：提出一种球形贮箱微重力环境下液体晃动的建模方法，可将微重力环境下球形贮箱内的液体晃动问题等效为三轴弹簧-质量系统的振动问题，可直接用于控制系统中实现控制系统设计。

本发明的技术解决方案是：一种球形贮箱微重力环境下液体晃动的建模方法，包括下列步骤：

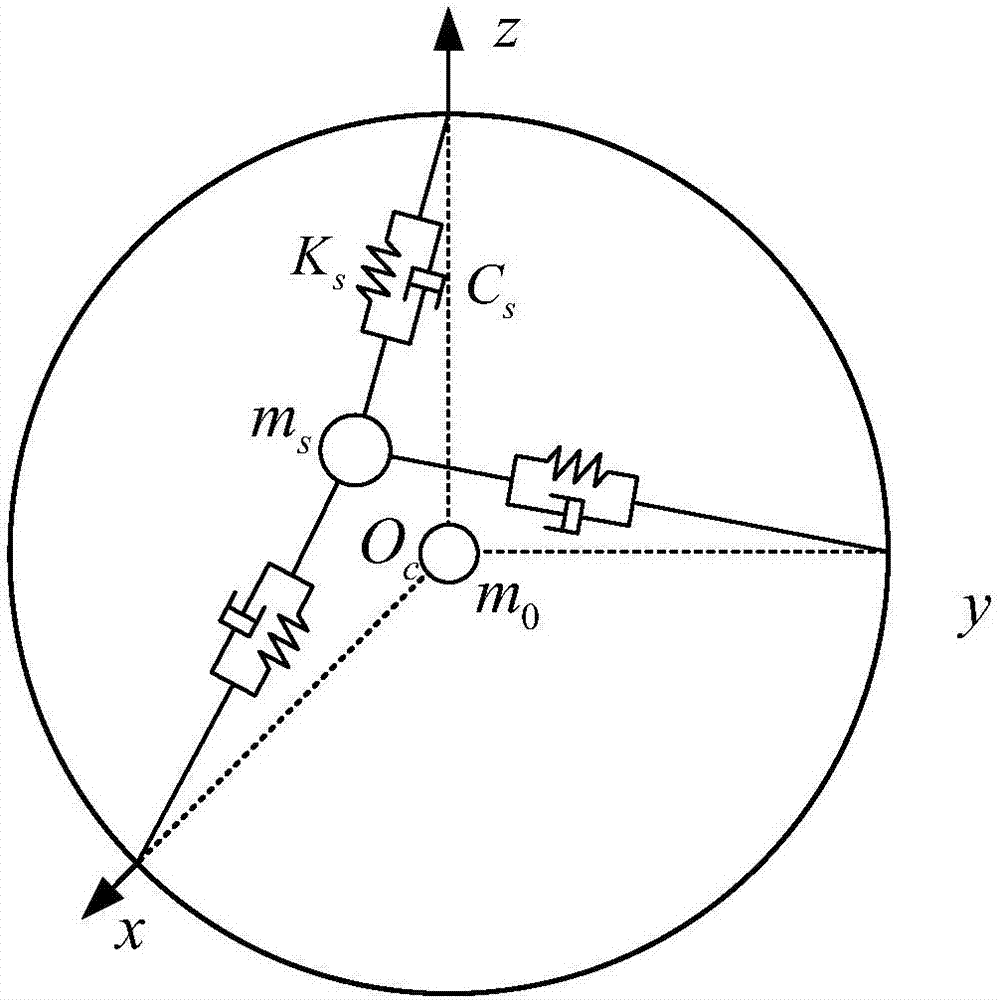
(1)、建立球形贮箱微重力环境下液体晃动的等效力学模型，所述等效力学模型为三轴弹簧-质量等效力学模型，它包含一个静止质量m0和一个晃动质量ms，其中，静止质量m0位于球形贮箱中心；晃动质量通过三个刚度系数为ks、阻尼系数为cs的弹簧阻尼器与贮箱连接，晃动质量处于平衡位置时，三个弹簧阻尼器方向分别与球形贮箱三轴重合；

(2)、计算球形贮箱零重力环境下液体晃动的n阶固有频率ω0i和模态φi，所述n≥1；

(3)、假设液体在微重力的作用下发生晃动，基于球形贮箱零重力环境下液体晃动的n阶固有频率ω0i和模态φi，推导贮箱内液体晃动时液体施加于贮箱壁面的作用力和液体相对贮箱晃动的动能，并依据其与步骤(1)中建立的等效力学模型作用力和动能等效原则，计算得到步骤(1)中所建立等效力学模型的晃动质量ms和静止质量m0。

所述步骤(2)的具体步骤为：

(2.1)、假设球形贮箱液体处于零重力环境下，液体在贮箱内形成一个处于全湿形态，内部有球形空腔的流体域，定义sf为液体自由液面，sw为固体壁面，sf和sw之间为流体域，球心至sf之间为空腔，球心至自由液面的距离为rm，f为自由液面发生波动时的波高；

(2.2)、建立(2.1)中所述流体域的流体动力学方程，获得流体域处于零重力环境下的自由液面sf上的动力学边界条件、自由液面上的运动学边界条件和贮箱壁面处的边界条件：

流体域处于零重力环境下的自由液面sf上的动力学边界条件为：

式中，δ为拉普拉斯算子,为流体域的势函数

自由液面sf上的动力学边界条件表示为：

式中，ρ是液体密度，σ为表面张力系数；

自由液面上的运动学边界条件为：

贮箱壁面处的边界条件为：

(2.3)、假设步骤(2.1)中所述流体域在球形贮箱内的小幅晃动为频率为ω的振动，将势函数和波高描述为：

式中，和f’为和f对时间的导数；

(2.4)、以球形空腔半径rm为特征长度，引入无量纲量r、f、φ、ω：

(2.5)、将步骤(2.2)中的势函数和波高f以步骤(2.3)的形式代入，并以步骤(2.4)中的无量纲形式进行整理，获得流体域无量纲形式的流体动力学方程、流体域在固体壁面处的边界条件和流体域在自由液面处的边界条件：

流体域无量纲形式的流体动力学方程：δφ＝0

流体域在固体壁面处的边界条件：

流体域在自由液面处的边界条件：

(2.6)、将步骤(2.5)中的三个方程写成galerkin变分形式方程：

式中：sw表示固体壁面，sf代表自由液面，v表示流体域δφ表示对φ取变分；

(2.7)、将步骤(2.6)中的方程前两项进行高斯变换，并将液体在自由液面处的边界条件简化为获得：

(2.8)、对流体域划分三维实体网格，在每个单元内有：

式中，代表φ在单元结点j处的值，nj为第j个单元的单元插值函数，ne为单元结点数；

(2.9)、将步骤(2.8)所得到φ代入至步骤(2.7)的公式中，根据变分的任意性推导得到单元刚度阵和单元质量阵：

单元刚度阵：

单元质量阵：

式中，j∈[1,ne]，k∈[1,ne]；

(2.10)、基于(2.9)，结合(2.8)划分的三维网格，利用有限元分析方法将单元刚度阵和单元质量阵组装成为整个流体域的液体刚度矩阵和液体质量矩阵，根据整个流体域的液体刚度矩阵和液体质量矩阵，通过特征值求解方法获得整个流体域的n阶ωi、φi和模态坐标qi，i∈[1,n]，所述n≥1；

(2.11)、计算流体域液体晃动的n阶固有频率ω0i和模态φi为：

所述步骤(3)的具体步骤为：

(3.1)、定义参考坐标系o0xyz和obxyz分别为惯性坐标系和贮箱本体坐标系，假设本体坐标系原点ob与球心oc重合，将势函数描述成：

式中，r为某液体质点相对于ob点的矢径，rb是ob相对于o0的矢径，φi和qi分别为第i阶液体晃动模态和模态坐标，n为参与计算的模态阶数；

(3.2)、计算液体对贮箱的作用力：

(3.2a)、依据步骤(3.1)得到的势函数形式，计算获得流场动压pd为：

为rb相对于时间变量t的二阶倒数，为模态坐标qi相对于时间变量t的一阶倒数；

(3.2b)、依据流场动压pd，计算液体对贮箱的作用力：

其中，n为贮箱壁面处的外法向单位矢量，mliq为流体域液体质量；

(3.3)、计算液体相对于贮箱晃动的动能：

(3.3a)、依据步骤(3.1)得到的势函数定义，获得流体速度u：

(3.3b)、计算液体相对于贮箱的动能：

(3.4)、计算等效力学模型产生的作用力和动能，采用步骤(2)所述的等效力学模型时，贮箱受到的作用力fe和等效力学模型相对于贮箱运动的动能te分别表示为：

式中，rs为晃动质量ms相对于oc点的矢径；

(3.5)、将步骤(3.3)和步骤(3.4)中获得的作用力和动能进行等效，即：f＝fe、t＝te，得到晃动质量ms和静止质量m0：

m0＝mliq-ms；

(3.6)、根据晃动质量ms、静止质量m0和流体域液体晃动的第1阶固有频率ω01，确定弹簧阻尼器的刚度系数ks和阻尼系数cs：

ks＝msω01²

步骤(3.6)中所述液体晃动阻尼比根据贮箱壁面边界层内和液体内部的平均能量耗散率dw和di得到：

式中，分别代表贮箱壁面边界层内和液体内部的平均能量耗散率，式中，ν为液体的粘度，u代表贮箱壁面附近的流体速度，r(φ)表示为：

本发明与现有技术相比的有益效果是：

(1)、本发明明确微重环境下贮箱内液体初始时刻为全湿形态，将微小的重力不作为过载处理，而当作外部激励处理，这样即可将微重力环境下的液体晃动问题转化为具有固有力学特性系统的受迫晃动问题，从而为等效力学模型的建立和求解奠定可行性基础。

(2)、本发明获得的三轴弹簧-质量等效力学模型，用晃动质量ms、静止质量m0、弹簧阻尼器的刚度系数ks和阻尼系数cs四个参数描述球形贮箱微重力环境下的液体晃动特性，该模型形式简单，可直接加入到航天器系统的动力学方程中，获得包含微重环境液体晃动的整星动力学方程。可应用于航天器的动力学预测以及控制系统的设计；

(3)、本模型中等效力学模型的晃动质量ms、静止质量m0、弹簧阻尼器的刚度系数ks和阻尼系数cs均通过理论推导获得，使用简单，实用性强。

附图说明

图1本发明实施例的微重力球形贮箱中的自由液面；

图2本发明实施例的球形贮箱三轴弹簧-质量等效力学模型示意图；

图3本发明实施例的球形贮箱等效系统动力学建模；

图4本发明实施例的微重环境小幅晃动力对比图；

图5本发明实施例的微重环境小幅晃动力矩对比图。

具体实施方式

以下结合附图和具体实施例对本发明进行详细描述。

球形贮箱微重力环境下液体晃动建模的困难在于如何将微重力环境下液体晃动这一流体动力学问题转化为等效力学振动问题，以描述微重力环境下液体晃动的频率特征及贮箱的受力特性。

球形贮箱内部液体处于微重力环境下时，液体在贮箱内处于全湿形态，形成球形的内部空腔，如图1所示，球形贮箱内部液体在外部激励的作用下发生小幅晃动。

本发明基于对球形贮箱在微重力环境下晃动特性的认识，提出了一种球形贮箱微重力环境下液体晃动的建模方法。该建模方法说明如下：

(1)、建立球形贮箱微重力环境下液体晃动的等效力学模型。

由于液体发生小幅晃动时，大部分液体仍将包裹在贮箱壁面上跟随贮箱一起运动，因此这部分液体用静止质量表示，其位置始终位于贮箱中心。将晃动质量看作质点，其平衡位置也位于贮箱中心，而液体小幅晃动用其相对于平衡位置的振动来描述。等效力学模型为三轴弹簧-质量等效力学模型，它包含一个静止质量m0和一个晃动质量ms，其中，静止质量m0位于球形贮箱中心；晃动质量通过三个刚度系数为ks、阻尼系数为cs的弹簧阻尼器与贮箱连接，晃动质量处于平衡位置时，三个弹簧阻尼器方向分别与球形贮箱本体坐标系三轴重合。如图2所示。

(2)、计算球形贮箱零重力环境下液体晃动的n阶固有频率ω0i和模态φi，所述n≥1。

(2.1)、假设球形贮箱液体处于零重力环境下，液体在贮箱内形成一个处于全湿形态，内部有球形空腔的流体域，定义sf为液体自由液面，sw为固体壁面，sf和sw之间为流体域，球心至sf之间为空腔，球心至自由液面的距离为rm，f为自由液面发生波动时的波高。如图1所示。

(2.2)、建立(2.1)中所述流体域的流体动力学方程，获得流体域处于零重力环境下的自由液面sf上的动力学边界条件、自由液面上的运动学边界条件和贮箱壁面处的边界条件。

(a)、建立球坐标系oc-rθα，坐标原点oc位于球心，依据势流理论，建立流体域的流体动力学方程，即流体域的势函数的laplace方程：

式中，δ为拉普拉斯算子,(r,θ,α)为流体域质点的球坐标，r为质点到原点的距离，θ为方位角，即质点与原点oc的连线与ocz轴正向的夹角，α为ocx轴按逆时针方向旋转到质点与原点oc的连线在oxy面上的投影时所转过的最小正角。

(b)、根据牛顿第二定律，获得自由液面sf上的动力学边界条件。

球坐标系下，自由液面上的二倍平均主曲率k表示为：

式中，div是散度算子，grad为梯度符号，也可用符号表示。

在静平衡状态下，二倍平均主曲率简化为km：

当液体发生小幅晃动时，可将k在静平衡液面附近展开，有：

因此，自由液面sf上的动力学边界条件表示为：

式中，ρ是液体密度，σ为表面张力系数。

(c)、自由液面上的运动学边界条件为以速度势函数形式表征的速度和波高形式表征的速度相等，即：

(d)、贮箱壁面处的边界条件即为贮箱壁面处的不可渗透条件：贮箱壁面处速度为0，即：

(2.3)、假设步骤(2.1)中所述流体域在球形贮箱内的小幅晃动为频率为ω的振动，将势函数和波高描述为：

式中，和f’为和f对时间的导数。

(2.4)、以球形空腔半径rm为特征长度，引入无量纲量r、f、φ、ω：

(2.5)、将步骤(2.2)中的势函数和波高f以步骤(2.3)的形式代入，并以步骤(2.4)中的无量纲形式进行整理，可获得流体域无量纲形式的流体动力学方程、流体域在固体壁面处的边界条件和流体域在自由液面处的边界条件：

流体域无量纲形式的流体动力学方程：δφ＝0

流体域在固体壁面处的边界条件：

流体域在自由液面处的边界条件：

(2.6)、将步骤(2.5)中的三个方程写成galerkin变分形式方程：

式中：sw表示固体壁面，sf代表自由液面，v表示流体域δφ表示对φ取变分。

(2.7)、将步骤(2.6)中的方程前两项进行高斯变换，并将液体在自由液面处的边界条件简化为获得：

(2.8)、对流体域划分三维实体网格，在每个单元内有：

其中代表φ在单元结点j处的值，nj为第j个单元的单元插值函数，ne为单元结点数。

(2.9)、将步骤(2.8)所得到φ代入至步骤(2.7)的公式中，根据变分的任意性推导得到单元刚度阵和单元质量阵：

单元刚度阵：

单元质量阵：

式中，j∈[1,ne]，k∈[1,ne]。

(2.10)、基于(2.9)，结合(2.8)划分的三维网格，利用有限元分析方法将单元刚度阵和单元质量阵组装成为整个流体域的液体刚度矩阵和液体质量矩阵，整个流体域的液体刚度矩阵和液体质量矩阵，通过特征值求解方法获得n阶ωi、φi和模态坐标qi，i∈[1,n]，所述n≥1。

(2.11)、计算流体域液体晃动的n阶固有频率ω0i和模态φi为：

(3)、假设液体在微重力的作用下发生晃动，基于球形贮箱零重力环境下液体晃动的n阶固有频率ω0i和模态φi，推导贮箱内液体晃动时液体施加于贮箱壁面的作用力和液体相对贮箱晃动的动能，并依据其与步骤(1)中建立的等效力学模型作用力和动能等效原则，计算得到步骤(1)中所建立等效力学模型的晃动质量ms和静止质量m0。

(3.1)、定义参考坐标系o0xyz和obxyz分别为惯性坐标系和贮箱本体坐标系，假设本体坐标系原点ob与球心oc重合，将势函数描述成：

式中，r为某液体质点相对于ob点的矢径，rb是ob相对于o0的矢径，φi和qi分别为第i阶液体晃动模态和模态坐标，n为参与计算的模态阶数。

(3.2)、计算液体对贮箱的作用力：

(3.2a)、依据步骤(3.1)得到的势函数形式，计算获得流场动压pd为：

为rb相对于时间变量t的二阶倒数，为模态坐标qi相对于时间变量t的一阶倒数。

(3.2b)、依据流场动压pd，计算液体对贮箱的作用力：

其中，n为贮箱壁面处的外法向单位矢量，mliq为流体域液体质量。

(3.3)、计算液体相对于贮箱晃动的动能：

(3.3a)、依据步骤(3.1)得到的势函数定义，获得流体速度u：

(3.3b)、计算液体相对于贮箱的动能：

(3.4)、计算等效力学模型产生的作用力和动能，采用步骤(2)所述的等效力学模型时，贮箱受到的作用力fe和等效力学模型相对于贮箱运动的动能te分别表示为：

式中，rs为晃动质量ms相对于oc点的矢径。

(3.5)、将步骤(3.3)和步骤(3.4)中获得的作用力和动能进行等效，即：f＝fe、t＝te，得到晃动质量ms和静止质量m0的表达式为：

m0＝mliq-ms

(3.6)、根据晃动质量ms、静止质量m0和流体域液体晃动的第1阶固有频率ω01，确定弹簧阻尼器的刚度系数ks和阻尼系数cs：：

ks＝msω01²

考虑粘性耗散作用，所述液体晃动阻尼比根据贮箱壁面边界层内和液体内部的平均能量耗散率dw和di得到：

其中分别代表贮箱壁面边界层内(即贮箱壁面至液体速度达到0.99倍主流速度的流体区域内)和液体内部的平均能量耗散率。式中，ν为液体的粘度，u代表贮箱壁面附近的流体速度，r(φ)表示为

这种建模方法与常重力环境下的弹簧-质量等效建模方法有很大区别。一方面，常重模型用来描述液体质心相对于贮箱的水平振动，因此通常包含水平方向上两个晃动方向互相垂直的的弹簧-质量系统，晃动质量共具有两个自由度；而三轴弹簧-质量模型可用来描述液体沿任意方向的运动，晃动质量具有三个自由度。另一方面，常重建模方法中由重力提供回复力，液体晃动的固有频率近似与成正比；而对于微重力环境，表面张力可以提供的回复作用很微弱，因此液体呈现出较弱的振动特性，其固有频率由表面张力系数决定。

实施例：

球形贮箱半径为r＝0.547m，充液比为25％，液体为常温下的水。通过计算获得其等效弹簧-质量模型，ms＝102.8kg，m0＝68.48kg，ks＝0.14425n/m，cs＝0.2827ns/m。

贮箱球心在本体坐标系下的坐标为(0.3,0.4,0.5)m，施加给贮箱沿x轴方向的平动激励和绕x轴方向的转动激励，运动规律分别为x＝0.01sin(0.1πt)m和θx＝0.01sin(0.2πt)rad。重力加速度沿z轴负向，大小为g＝10^-5m/s²。获得液体对贮箱的作用力如图4和如5所示。图4和图5同样画出了利用商用软件flow-3d在同样的激励条件下计算同样的贮箱的响应。对比结果表明，误差小于10％。采用本方法计算获得液体对贮箱的作用力耗时仅十多分钟，而采用flow-3d计算需要数小时。

本发明未详细描述内容为本领域技术人员公知技术。