一种多约束条件下椭圆轨道卫星编队构形初始化方法与流程

本发明涉及一种卫星编队构形初始化方法，尤其涉及一种在多约束条件下建立椭圆轨道卫星编队的最优初始化方法，属于航天器制导与控制领域。

背景技术：

近年来，卫星编队技术因其未来广阔的应用领域而备受关注。基于小卫星的卫星集群编队飞行技术以其强大的技术优势和广阔的应用前景，得到了军事、工业、商业以及科研等领域相关机构的普遍关注和认可。双星编队是最基本的卫星编队形式，编队由主星和从星组成，从星环绕主星执行在轨监测任务，例如可以检测主星的外形结构、太阳帆板是否正常，从而降低成本并减少航天员在舱外活动的风险性。同时，绕飞监测也是实现对目标航天器进行燃料加注、在轨维修、物资补给、空间交会等在轨服务的重要助益和关键技术。因此，有关卫星编队的绕飞构形设计以及构形初始化控制的研究有着十分重要的意义。

卫星编队的构形和控制是以相对动力学为基础，圆轨道相对运动模型由c-w方程给出。当目标航天器运行的轨道为椭圆形轨道时，由于轨道偏心率的存在，c-w方程会引入明显的误差，此时采用t-h方程来描述其线性相对运动。然而，由于在时域内t-h方程具有显著的非线性特征，相对运动的求解十分困难，为此本发明通过真近点角域变换来线性化t-h模型，并推导出解析解。

编队卫星释放过程中的控制一般采用有限幅值的推力器，且为了保证释放过程中的安全性，一般需要采用可见光相机进行监测，因此在编队初始化时，必须考虑上述工程约束条件。轨迹优化问题的求解，从本质上可分为间接法、直接法以及混合法。间接法在理论上严格满足最优性一阶必要条件，但在实际计算过程中，由于对协状态初始猜测的高度敏感性，收敛半径很小，求解比较困难，因此应用受到了一定的限制。直接法相比间接法，可以有效避免协状态的求解，且可以通过适当选取离散节点的规模，有效减少计算量。

技术实现要素：

本发明公开的一种多约束条件下椭圆轨道卫星编队构形初始化方法要解决的技术问题是：在多约束条件下实现椭圆轨道卫星编队构形初始化，通过卫星编队构形初始化实现在多约束条件下的有效最优控制。

本发明的目的通过以下技术方案实现。

本发明公开的一种多约束条件下椭圆轨道卫星编队构形初始化方法，包括如下步骤：

步骤一：通过经典轨道动力学和坐标变换，推导得出真近点角域t-h方程解析解。

步骤1.1：分别建立惯性坐标系和轨道坐标系；

建立以地球为中心的固定惯性坐标系，其x轴指向春分点，z轴与地球的旋转轴方向一致，y轴根据右手定则确定。建立以主星为质心相对于原点旋转的轨道坐标系，其x轴从地球中心指向主星的中心，z轴垂直于轨道平面，y轴根据右手定则确定。

步骤1.2：根据经典轨道动力学得出解析解；

定义主星与从星的相对位置矢量ρ＝rd-rc，其中rd∈r³和rc∈r³分别是从星和主星的位置矢量。主星和从星之间的相对动力学在惯性参考系中表示为：

其中μ表示恒定的地球重力系数，而u∈r³表示由固定在追踪器上的推进器产生的主动控制加速度。由惯性参考系向轨道坐标系转换，式(1)近似表述为：

其中ω是主星的轨道角速度，下标o表示旋转轨道坐标系内描述的矢量。将式(1)代入到式(2)中，相对运动表示为

其中

其中f是主星的真近点角。最后，将公式(1)、(2)带入到式(3)中得到：

其中

若忽略主动控制，式(5)至(7)即为t-h方程。t-h方程描述两航天器的自由绕飞相对动力学，且轨道面内外运动是解耦的。由于t-h方程的非线性，很难在时域中找到t-h方程的解析解。因此，通过以下转换重新改写t-h方程：

取f一阶和二阶导数，

定义如下运算符：

最后，将式(9)到(13)代入到式(5)到(7)中，则相对动力学重新表示为：

显然，式(14)-(15)是线性化的，且在给定的初始条件下解得：

其中

h和p分别是主星的角动量和正半焦距。ci(i＝1,2,...,6)是由主星的初始状态和初始真近点角所确定的常系数，按下式计算：

t-h方程解析解为即实现推导得出真近点角域t-h方程解析解。

步骤二：推导周期性绕飞约束条件，建立监测相机视场约束和推力幅值约束。

步骤2.1：导出真近点角域中的周期性绕飞约束条件；

由于式(21)至(26)都是正弦曲线，因此，对于给定的真近点角f，若c4(f)＝0，即

则能够确保得到周期性相对轨迹。此外，由式(9)(10)和(27)有：

式(28)是任意椭圆轨道中周期轨迹的必要条件，并且如果满足式(27)，相应的周期性相对运动表示为

然而，式(27)无法保证是周期性绕飞轨迹，因此改写式(30)如：

然后，结合式(32)与式(29)，面内相对轨迹表示为

当面内轨迹绕飞时，能够确保三维轨迹绕飞。在式(33)中，当c1＝0时，绕飞轨迹简化为以(0,0)为中心的椭圆，且其半轴随着时间而变化。故周期性绕飞约束条件描述为：

其中k是根据绕飞轨迹选择的系数，若期望从星遵循平面内相对轨迹，则可以设置k为零。

步骤2.2：建立监测相机视场约束。

为了确保编队构形初始化的安全，主星上安装可见光相机来监测从星释放过程，从星位于相机的视场内，直到从星形成周期性绕飞轨迹。监视摄像机的fov几何结构由两个锥体组成，点ot是两个锥体的顶点交点，表示镜头的光学中心，l是几何结构的中心轴，表示光轴，矩形abcd是下锥体的底，表示ccd阵列，并且α和β是fov角，fov角α和β是由ccd的大小和镜头的焦距确定的。fov的范围由锥体o-a′b′c′d′表示，但是具有无限的深度。视场的范围由锥体表示，同样也具有无限的深度，监视坐标系表示为固定在镜头的光学中心上的非旋转坐标系。因此，从点ot到主星的质心的距离极小，忽略ot到主星的质心的距离，因此，监视坐标系与主星的体坐标系一致。

考虑到点的位置矢量有：

然后平面oa′d′可以表示为：

其中下标b表示在体坐标系中描述的矢量。类似地，其他三个平面的方程表示为：

因此，监视约束表示为：

此外，在轨道坐标系中假设主星的姿态是(θφψ)^t。其中θ，φ和ψ分别是俯仰角，偏航角和滚转角，然后体坐标系中的矢量转换为轨道坐标系，如公式(40)所示：

其中lob(θ,φ,ψ)是从体坐标系到轨道坐标系的变换矩阵。将式(40)代入式(39)，在轨道坐标系中得到监视约束

步骤2.3：建立电力推进的幅值约束；

由于电动推进器固定在从星上，从星的姿态运动导致推力方向相对于轨道坐标系发生变化，使得构形初始化明显变得更复杂，因此，通过从星应相对于轨道坐标系保持恒定的姿态对构形初始化进行简化，并且推力加速度总是沿着轨道坐标系的轴线，因此电力推进幅值约束表示为：

其中表示每个方向上推力的最大幅值。

步骤三：基于步骤一推导得出的真近点角域t-h方程解析解，以及步骤二建立的监测相机视场约束和推力幅值约束，建立编队的多约束最优控制模型。

步骤3.1：在不考虑约束条件下，建立基本的最优控制模型；

一般形式的非线性最优控制表示为：在时间区间[t0,tf]内，找到最小化性能指标泛函的状态控制函数

同时状态受到系统动力学方程约束

边界约束

ψ(x(t0),x(tf))＝0(45)

以及存在的状态和控制混合的路径约束

c(x(t),u(t))≥0(46)

其中e称为终端性能指标，也称mayer型性能指标；含有f的积分项称为过程性能指标，也称lagrange型性能指标。定义增广hamilton函数为

l(x(t),u(t),λ,μ)＝h(x(t),u(t),λ)+μ^tc(x(t),u(t))(47)

其中λ是协状态变量，h是hamilton函数

h(x(t),u(t),λ)＝λ^tf(x(t),u(t))+f(x(t),u(t))(48)

且μ满足互补条件

μ^tc(x(t),u(t))＝0(49)

故最优控制与状态通过求解下列方程得到：

其中上标*表示满足前述约束条件的最优解。

步骤3.2：基于步骤二建立的监测相机视场约束和推力幅值约束，建立多约束最优控制模型；

考虑真近点角的角速度和角加速度

其中，代表平均轨道角速度，而a和e分别表示轨道的半长轴和偏心率。然后把式(52)代入式(5)和(6)，则增广的动力学方程重新表述为：

其中表示增广动力学，而代表增广状态向量。所述式(34)中表达式被视为对增广动力学的非线性状态约束，使得能够通过使用直接方法来解决问题。

一旦编队构形开始，从星就会被释放，构形的初始状态由释放位置和速度决定，即

编队构形的最终状态受到周期性绕飞约束：

其中ci(i＝1,2,...,6)根据式(21)至(26)计算所得，在构形期间，从星必须位于主星ccd相机的fov中，即根据式(41)，相对状态应满足以下约束条件：

每个轴上的推力也应满足以下约束条件：

故多约束最优控制问题的数学描述为：

式(58)受到式(53)的动力学约束、式(54)的初始状态约束、式(55)的周期绕飞约束、式(56)的fov约束和式(57)的推力幅值约束。

步骤四：求解多约束最优控制模型，得到原最优控制问题的解，继而得到任意时刻的协态值，即在多约束条件下实现椭圆轨道卫星编队构形初始化，通过卫星编队构形初始化实现在多约束条件下的有效最优控制。

步骤四所述的求解建立编队的多约束最优控制模型的方法包括直接法、间接法和混合法。

高斯伪谱法是一种直接法，在求解过程中其与最优控制理论中的一阶必要条件是一致的；另一方面，根据协状态映射原理，高斯伪谱法能够得到与最优控制理论相同的协状态信息，因此，步骤四所述的求解建立编队的多约束最优控制模型的方法优选高斯伪谱法求解，当用高斯伪谱法求解建立编队的多约束最优控制模型，步骤四具体实现方法包括如下步骤：

步骤4.1：高斯伪谱法求解；

高斯伪谱方法的基本思路为，将未知的状态时间历程与控制时间历程在一系列高斯点上离散，之后用所述离散的状态与控制分别构造拉格朗日插值多项式去逼近真实的状态与控制的时间历程，并借助简单的数学知识将动力学微分方程约束转化为一系列代数约束，最优控制问题最终转化为受一系列代数约束的参数优化问题，再利用其他数值方法如序列二次规划法求解。

高斯点为勒让德多项式的零点，不均匀分布在区间[-1,1]，因此必须对真实的时间区间t∈[t0,tf]进行转化：

转换后τ取代t成为独立变量，t0,tf成为系统参数。相应地，原时域最优控制问题在τ域表述为：

使用第k个勒让德-高斯点和初始节点处的状态，导出具有k+1阶的拉格朗日插值多项式：

其中

拉格朗日插值能够确保插值节点处的近似与实际状态完全相同，而其他点处的值仅近似相等。类似地，使用第k个勒让德-高斯点的控制，控制的拉格朗日插值多项式导出为

其中

区分方程式中的式(61)得到

其中微分矩阵确定如下：

其中k＝1,2,...,k和i＝0,1,...,k，pk(τ)表示k阶的勒让德多项式，即

将式(67)代入式(66)，将动力学约束代数化为

终端值应通过高斯求积法获得

其中ωk为高斯权重，计算为

ωk和dki仅由lg点k的数量确定，并且在优化算法之前离线计算求解，式(60)的连续性能指标泛函用高斯积分解得：

故由高斯伪谱方法，最初的最优控制问题被转化成了一个非线性规划问题，描述如下：

求解这个非线性规划问题即得到原最优控制问题的解，并且得到任意时刻的协态值，即在多约束条件下实现椭圆轨道卫星编队构形初始化，通过卫星编队构形初始化实现在多约束条件下的有效最优控制。

有益效果：

本发明公开的一种多约束条件下椭圆轨道卫星编队构形初始化方法，通过经典轨道动力学和坐标变换，推导得出真近点角域t-h方程解析解，并分析动力学约束，周期性绕飞约束，建立监测相机视场约束和推力幅值约束，从而建立编队的多约束最优控制模型并通过高斯伪谱法求解，得到任意时刻的协态值，实现对航天器结构完整性的实时监视，且通过增加偏心率和初始化时间降低推进系统的燃料消耗和最大幅值。

附图说明：

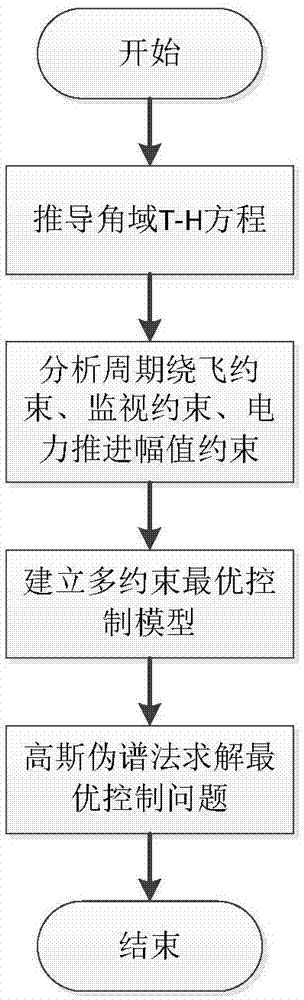
图1为本发明一种多约束条件下椭圆轨道卫星编队构形初始化方法的流程图；

图2为本发明双星编队坐标系示意图；

图3为本发明步骤二fov几何结构图；

图4为本发明步骤二fov约束条件示意图；

图5为本发明从星释放轨迹与绕飞轨迹；

图6为本发明从星释放轨迹与绕飞轨迹在x-y面的投影；

图7为本发明从星释放轨迹与绕飞轨迹在y-z面面的投影；

图8为本发明从星相对位置的时间历程；

图9为本发明从星相对速度的时间历程；

图10为本发明从星各向最优推力加速度的时间历程；

具体实施方式

为了更好地说明本发明的目的和优点，下面结合附图对本发明的具体实施方式作进一步详细的说明。在整个仿真过程中，忽略所有轨道摄动，同时认为主星的轨道姿态全程不发生变化，释放前从星固定在主星上，编队初始化过程由弹射装置开启，之后从星进入预定的相对绕飞轨道。仿真在matlab环境下使用gpops-ii工具箱将原最优控制模型转化为一系列非线性规划问题(nlp)，再使用snopt软件完成最终的求解。

实施例1：

本实施例公开的一种多约束条件下椭圆轨道卫星编队构形初始化方法，参考轨道的参数如下：半长轴a＝8378km，倾角i＝15°，升交点赤经ω＝45°和近地点角距ω＝30°。在控制开始时，假设初始真近点角f0＝0，周期绕飞约束内的参数k为0.5，并且监视相机的fov范围是60°×60°。从星是质量为10千克的微型卫星，配备有三维电力推进装置，每个方向的推力最大幅值为100mn。释放所用的时间(表示为tf)设置为1500秒，从星的初始状态为轨道偏心率e＝0.05。

步骤一：通过经典轨道动力学和坐标变换，推导得出真近点角域t-h方程解析解。

如图2所示，建立以地球为中心的固定惯性坐标系，其x轴指向春分点，z轴与地球的旋转轴方向一致，y轴根据右手定则确定。建立以主星为质心相对于原点旋转的轨道坐标系，其x轴从地球中心指向主星的中心，z轴垂直于轨道平面，y轴根据右手定则确定。根据经典轨道动力学，将半长轴a＝8378km，倾角i＝15°，升交点赤经ω＝45°和近地点角距ω＝30°等数据代入式(17)(18)(19)得出解析解

步骤二：推导周期性绕飞约束条件，建立监测相机视场约束和推力幅值约束。

步骤2.1：导出真近点角域中的周期性绕飞约束条件；

步骤2.2：建立监测相机视场约束；

如图3和图4所示，监视摄像机的fov几何结构由两个锥体组成，点ot是两个锥体的顶点交点，表示镜头的光学中心，l是几何结构的中心轴，表示光轴，矩形abcd是下锥体的底，表示ccd阵列，并且α和β是fov角，fov角α和β是由ccd的大小和镜头的焦距确定的。fov的范围由锥体o-a′b′c′d′表示，但是具有无限的深度。视场的范围由锥体表示，同样也具有无限的深度，监视坐标系表示为固定在镜头的光学中心上的非旋转坐标系。因此，从点ot到主星的质心的距离极小，忽略ot到主星的质心的距离，因此，监视坐标系与主星的体坐标系一致。

步骤2.3：建立电力推进的幅值约束；

步骤三：基于步骤一推导得出的真近点角域t-h方程解析解，以及步骤二建立的监测相机视场约束和推力幅值约束，建立编队的多约束最优控制模型。

步骤3.1：在不考虑约束条件下，建立基本的最优控制模型；

步骤3.2：基于步骤二建立的监测相机视场约束和推力幅值约束，建立多约束最优控制模型；

步骤四：求解多约束最优控制模型，得到原最优控制问题的解，继而得到任意时刻的协态值，即在多约束条件下实现椭圆轨道卫星编队构形初始化，通过卫星编队构形初始化实现在多约束条件下的有效最优控制。

步骤4.1：高斯伪谱法求解；

将真近点角f0＝0，周期绕飞约束内的参数k为0.5，监视相机的fov范围是60°×60°。从星是质量为10千克的微型卫星，配备有三维电力推进装置，每个方向的推力最大幅值为100mn。释放所用的时间(表示为tf)设置为1500秒，从星的初始状态为轨道偏心率e＝0.05等各约束条件代入是(72)，获得最优解j＝0.0067。图5显示了轨道坐标系中从星的构形和周期性绕飞轨迹，图5中的四角锥表示相机的fov。

图4显示最佳释放轨迹始终位于四角锥内，直到从星进入周期性绕飞轨道，这使得从星能够进行实时监视，以确保编队构形的安全性，并且轨迹也是平滑的，在释放期间没有观测到振荡。释放1500秒终止后，从星通过遵循期望的周期绕飞轨迹连续移动，这也证明了当初始化椭圆轨道中的周期性绕飞相对运动时，式(55)中约束的正确性。

图6和图7表示x-y和z-y平面中的轨迹投影：由于参考轨道的偏心率很小，两个平面中的闭合投影近似椭圆，这与式(33)所得出的结论一致。从星的相对位置和速度的时间历程分别如图8和图9所示，在释放过程中，相对位置和速度从初始值平滑变化到所需的最终值，相对速度的峰值分别为0.85m/s(x方向)，1.5m/s(y轴负方向)和0.47m/s(z方向)。

如图10所示，最优推力加速度在整个释放过程中也从正值平稳地变化到负值，并且推力加速度的最大幅值在1500s的x轴上发生，但推力加速度三个方向都不会超过最大幅值的30％。

综上所述，以上仅为本发明的较佳实施例而已，并非用于限定本发明的保护范围。凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。