基于量子退火的混合整数最优控制数值求解方法与流程

本技术涉及利用量子退火算法求解混合整数最优控制问题，具体地说是一种基于量子退火的混合整数最优控制数值求解方法。

二、

背景技术：

最优控制研究的主要问题是：在满足动态约束条件下，寻求最优控制策略，使得问题性能指标取极大值或极小值。它属于最优化的范畴，与最优化有着共同的性质和理论基础。这类问题广泛存在于各种技术领域和社会问题中。混合整数最优控制问题是指包含整数决策变量的最优控制问题。该问题属于既包含整数决策变量又包含浮点数控制变量的组合优化问题，在智能城市、智能仓储、化工生产等领域应用极广。但由于求解最优整数决策变量的计算复杂性，混合整数最优控制问题一直是控制和优化领域的棘手问题。因此，研究混合整数最优控制问题就显得尤为重要。

目前混合整数最优控制问题的求解方法大致分为：解析法，间接法，直接法(控制变量参数化方法、联立法)等。其中，解析法主要采用基于变分的最优性必要条件或动态规划理论解析获得问题的解。由于只能求解简单问题，此方法在理论上有指导意义，但一般无法应用于实际。间接法与解析法类似，也是一种基于最优性必要条件的求解方法。根据极大值原理，最优性必要条件可以表述为一个两点边值问题，因此间接求解方法实际为求解微分方程组的两点边值问题。通常对于问题描述较为复杂或者无明确数学表述的混合整数最优控制问题，解析法或间接法并不适用，此时可采用直接法进行求解。

直接法的基本思想是采用一定的参数化技术将问题轨迹在时间域进行离散化，从而实现最优控制问题的静态非线性规划表述，之后采用优化算法实现问题求解。遗传算法、粒子群算法、模拟退火等智能优化算法都是处理该问题的合适工具，但是这些算法或多或少都有局部搜索能力差或收敛速度慢等缺点。量子退火是通过使用量子波动的过程在给定的一组候选解(候选状态)上找到给定目标函数的全局最小值的元启发式算法。它作为一种高效新颖的算法以操作原理简单，参数较少和易实现等特点优于上述诸多智能优化算法。量子退火主要用于搜索离散空间中的整数变量来求解整数规划问题，因此它非常适合求解混合整数最优控制问题。具有收敛速度快、不易陷入局部最优解等特点。

三、

技术实现要素：

本发明提出一种基于量子退火的混合整数最优控制数值求解方法，针对一个混合整数最优控制问题，首先建立混合整数最优控制模型，然后利用控制向量参数化和四阶Runge-Kutta方法将混合整数最优控制模型转化成混合整数非线性规划模型。其次，对比于传统智能优化算法，提出收敛速度更快、全局搜索能力更强的量子退火算法，利用量子退火算法求解整数决策变量，对于最优浮点数控制变量，采用并行差分进化算法进行求解；最后通过两部分交互迭代优化获得最优混合整数控制决策。

本发明的目的通过以下技术方案来实现：

该种基于量子退火的混合整数最优控制数值求解方法，包括以下步骤：

1.建立混合整数最优控制模型

对于一个混合整数最优控制问题，首先要对其进行建模。本专利给出一个一般形式的混合整数最优控制模型如下所示：

a(x(tf)，tf)＝0，

g(x(t)，u(t)，w(t)，t)≤0，

umin≤u(t)≤umax，w(t)∈Z^w，

其中，t为时间，J为性能指标，x(t)∈Rⁿ为状态变量，u(t)∈R^u为浮点数控制变量，w(t)∈Z^w为整数决策变量，x0为初始状态变量，为关于末端时刻状态变量的函数，为关于控制变量和状态变量的泛函，为微分方程约束，为末端时刻的等式约束，为路径约束，to和tf分别是起始时间和末端时间，umin和umax是u(t)的边界条件。求解该模型即是求解混合整数最优控制变量u(t)和w(t)使系统在约束条件下实现性能指标的最小化。

2.将模型转化成混合整数非线性规划模型

对于上述的混合整数最优控制模型，采用直接法对其进行转化处理，主要包括：使用控制向量参数化对控制向量u(t)和w(t)进行离散；对于状态变量x(t)，使用四阶Runge-Kutta方法对其进行离散处理。将最优控制模型转化成非线性规划模型。

具体步骤：

(1)控制向量参数化

对于一个连续时间域上的控制变量u(t)和w(t)，无法直接求解其控制轨迹，需要将其参数化处理转化成多个离散变量。将全部时间域[t0，tf]分成N个子区间：

t0＜t1＜...＜tk-1＜tk＜tk+1＜...＜tN＝tf，k＝1，2，3，...，N-1，

其中，每个子区间的长度Δtk＝tk-tk-1可以相等或不等。一般来说，均分法计算量较小但误差较大，采用非均分法则需要将N个间隔长度也看作控制变量进行求解，计算量较大但是相对误差较小，也更贴近实际最优控制轨迹。

在每个区间[tk-1，tk]上，选取一个代表映射关系的基函数bk，它可以被有限个控制参数qk进行参数化，以确保离散的可分离性。常用的基函数主要包括下列三种形式：

分段常数

分段线性函数

分段样条函数(β为样条函数系数)；

不同基函数的选取会导致离散形式的不同，因此需要根据不同的实际最优控制问题以选取相应的基函数。通过控制向量参数化，将连续的控制变量转化成离散的控制变量如下所示：

u(t)＝uk(t)＝αkbk，w(t)＝wk(t)＝βkbk，t∈[tk-1，tk]，

其中，αk和βk是待求的系数。

(2)四阶Runge-Kutta方法

本发明采用四阶Runge-Kutta方法对状态变量x(t)进行离散化处理，它对比于传统的欧拉法，局部截断误差更小，离散结果更准确。在每个区间[tk-1，tk]上，x(t)的计算过程如下所示：

a.计算k1＝f(xk，uk，wk)及其偏导数：

b.计算及其偏导数：

c.计算及其偏导数：

d.计算k4＝f(xk+hk3，uk)及其偏导数：

e.计算下一个子区间的状态变量及其偏导数：

通过上述计算过程，连续时间域的状态变量x(t)转化成了离散的xk以便于后续的模型转换及计算求解。

(3)建立混合整数非线性规划模型

引入一个新变量z满足z(t0)＝0.定义X(t)＝[x(t)^Tz(t)]^T和F(t)＝[f(t)^TL(t)]^T。原最优控制模型转化成如下非线性规划模型：

s.t.Xk+1(t)＝F(Xk(t)，uk(t)，wk(t)，t)，t∈[tk-1，tk]，k＝1，2，...，N，X1(t0)＝X0，

a(X(tf)，tf)＝0，

g(Xk(t)，uk(t)，wk(t)，t)≤0，t∈[tk-1，tk]，k＝1，2，...，N，

umin≤uk≤umax，wk∈Z^w.

为了方便计算，本发明对其进行标准化处理。引入标准化时间变量τk∈[0，1]满足第k个子系统表示为：

因此，混合整数最优控制模型转化成混合整数非线性规划模型如下所示：

a(X(τN(1))，τN(1))＝0，

umin≤uk(τ)≤umax，wk(τ)∈Z^w.

它是一个约束优化模型，本发明使用罚函数法对其进行处理从而转化成一个无约束优化模型：

其中，μi(i＝1，2，3，4)为无穷大的惩罚因子。通过本步骤的计算处理，原混合整数最优控制模型转化成了混合整数非线性规划模型。

3.提出量子退火算法

基本思想为：建立包括动能项和势能项的哈密尔顿函数式，利用格雷码对整数决策变量进行编码，然后确定自旋矩阵和变异算子，通过动能项的变化提供扰动从而完成一个退火过程，最后迭代搜索得到最优的自旋矩阵即整数决策变量。

具体步骤：

(1)建立哈密尔顿函数式：H＝Hpot/P+δΔHkin，其中P为自旋矩阵个数，Hpot是总势能项，Hkin是动能项，δ＝-T/2ln tanh(Γ/PT)是铁磁耦合项，其中T为温度，Γ为隧穿场强系数，PT记为有效量子温度。在哈密尔顿函数式中，势能项Hpot通常为模型的性能指标J。

(2)格雷编码：利用格雷码对整数决策变量进行编码。对于一个任意的二进制数Bn-1Bn-2…B2B1B0，(Bi∈{0，1}，i＝0，1，...，n-1)，都有一个与之对应的格雷码Gn-1Gn-2…G2G1G0，(Gi∈{0，1}，i＝0，1，...，n-1)。两者之间的转换公式如下所示：

Gn-1＝Bn-1，i＝0，1，2，...，n-2，

其中，表示异或操作。使用格雷编码可以有效的防止在迭代过程中的“数据断崖”现象，既节约了收敛时间又可以加强算法的全局搜索能力。

(3)建立自旋矩阵群体：建立由P个自旋矩阵W所组成的自旋矩阵种群，每个矩阵都代表着一个整数决策变量集，种群中的第z个个体记为W^z。每个自旋矩阵W都是一个q×k维的对称矩阵，其中，k是待求整数决策变量的数量，q是整数变量经过格雷编码后的位数。因此，自旋矩阵W即代表整数决策变量的集合。构建如下自旋矩阵：

其中，w1表示第一个整数变量，向量A＝[w2，w3，...，wk-1]表示其他k-1个整数变量。由于自旋矩阵必须为对称阵，因此除了第一行(列)的元素以外，矩阵的其余元素都记为0。通过迭代搜索获得最优自旋矩阵W即可得到最优整数决策变量w(k)。

(4)选取变异算子：对于第z个自旋矩阵W^z，设置N个变异算子用来在迭代过程中更新候选矩阵W^z，变异算子通过模拟量子隧穿效应对自旋矩阵进行如下操作：随机选取两个整数变量并交换它们的值；随机选取一个整数变量中两个位并交换它们的值；随机选取一个整数变量，对其中的任意位数值取“逆”操作。通过变异算子对候选矩阵的改变，从而实现淘汰次优解，获得更优解。模拟量子隧穿效应的变异算子具有一个跳出当前搜索区域的机制，因此可以更好的防止搜索过程陷入局部极值。

(5)提供扰动：在量子退火算法的迭代过程中，由动能项Hkin的改变提供一个扰动以促使退火过程的进行。动能项的计算需要首先获知每个自旋矩阵及其相邻自旋矩阵的状态，即

其中，表示第z个自旋矩阵的第i个整数变量。表达式的第一项为当前个体W^z与前一个个体W^z+1中所有元素的乘积和；同理，表达式的第二项为当前个体W^z与后一个个体W^z+1中所有元素的乘积和。ΔHkin可以表示为：

其中，表示第z个矩阵变异后得到的自旋矩阵W^z′的第i个整数变量。这样，在退火过程中通过改变动能项Hkin从而改变哈密尔顿函数式，为淘汰劣解提供判别依据。

(6)计算哈密尔顿函数式增量：利用变异后的自旋矩阵计算新的性能指标，结合原性能指标计算两者差值ΔJ。利用动能项的增量ΔHkin计算哈密尔顿函数式增量ΔH＝(ΔJ/P)+δΔHkin。

(7)选择：如果ΔJ≤0或ΔH≤0，将变异后的自旋矩阵W^z′赋值到W^z；随机设定一个数Θ∈(0，1)，如果exp(-ΔH/T)＞Θ，那么也将变异后的自旋矩阵W^z′赋值到W^z，这提供了一个次优解也可以一定概率进入下一代的机制以防止搜索陷入局部极值。记录W^z，更新相应参数，跳转到步骤(4)利用W^z进行新的迭代。

(8)判断是否满足终止条件，如果满足，结束循环，如果不满足，跳转到步骤(4)继续执行。

4.利用基于量子退火的数值求解算法计算混合整数非线性规划

具体过程为：

(1)设定初始浮点数变量：在浮点数变量u(k)的可行域中随机选取一个浮点数变量带入混合整数非线性规划模型中，将模型转化成整数非线性规划模型。记u^o(k)为最优浮点数变量；

(2)格雷编码：利用格雷码对整数决策变量进行编码；

(3)建立初始自旋矩阵种群：建立由P个自旋矩阵W所组成的自旋矩阵种群，每个矩阵都代表着一个整数决策变量集，种群中的第z个个体记为W^z；

(4)种群变异：从N个变异算子中随机选取一个对自旋矩阵种群执行变异操作，得到新的自旋矩阵种群；

(5)提供扰动：利用原矩阵种群中的个体W^z和变异矩阵种群中的个体W^z′计算得到动能项的增量ΔHkin。利用动能项的增量ΔHkin计算哈密尔顿函数式差值ΔH＝(ΔJ/P)+δΔHkin；

(6)选择：满足集合Ω＝{ΔJ≤0，ΔH≤0，exp(-ΔH/T)＞random(0，1)}中任意一个条件，则将变异后的自旋矩阵W^z′赋值到W^z，更新相应参数；

(7)判别整数变量中止条件：判断是否满足终止条件，如果满足，结束循环，如果不满足，跳转到步骤(4)继续执行，直到得到最优整数决策变量W^o；

(8)建立初始浮点数变量种群：将最优整数决策变量W^o带入混合整数非线性规划模型，将原模型转化成一个浮点数非线性规划模型。建立规模为NP的浮点数变量种群，种群中的第i个个体在第G代记为其中D是个体所包含的维度，NP＝30D，种群初始化采用公式xj，i，0＝xj，min+randi，j(0，1)×(xj，max-xj，min)，其中xj，i，0表示第G＝0代，种群中第i个个体，第j个维度的值；

(9)参数和种群变异：针对两个种群的控制参数和种群，对缩放因子进行自调整。对种群采用DE/current-to-pbest/1的差分变异策略；

(10)计算适应度函数：将各个控制策略代入非线性规划模型，以性能指标作为适应度函数值；

(11)选择：将每个种群的各个控制策略相应的适应度函数作比较，保留适应度函数最小的控制参数和种群个体存入相应库中，更新相应参数；

(12)判别浮点数变量中止条件：判断是否满足终止条件，如果满足，结束循环，如果不满足，跳转到步骤(9)继续执行，直到得到当前最优浮点数变量u(k)为止，更新u^o(k)；

(13)交互式迭代搜索：将u(k)带入原混合整数非线性规划模型，将其转化成整数非线性规划模型。跳转到步骤(3)；

(14)判别局部最优解条件：判断所得最优浮点数变量是否等于u^o(k)，如果不满足，跳转到步骤(13)，如果满足，说明W^o和u^o(k)即为一个局部最优解，记录W^o和u^o(k)；

(15)判别终止条件：判断是否满足终止条件，如果满足，结束循环，如果不满足，更新u^o(k)，跳转到步骤(1)，进行全局最优解搜索，直到得到最优控制策略结束循环为止。

四、附图说明

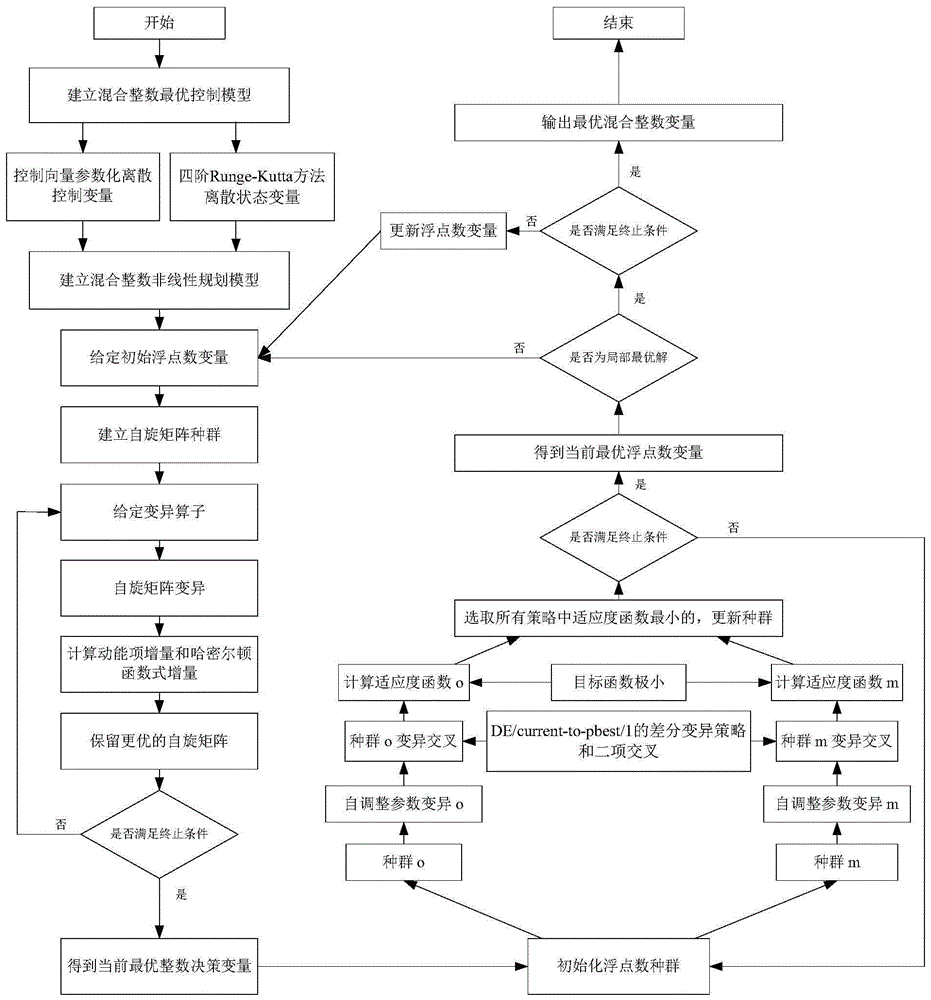
图1是本发明的流程示意图

图2是量子退火算法流程图

五、具体实施方式

下面结合附图对本发明作进一步描述：

参照图1，本发明基于量子退火的混合整数最优控制问题数值求解方法具体实施过程如下：

(1)基于实际最优控制问题，建立既包含整数决策变量又包含浮点数控制变量的混合整数最优控制模型；

(2)对于构建好的最优控制模型，利用控制向量参数化对混合整数控制变量进行参数化处理，使用四阶Runge-Kutta方法将状态变量离散。通过控制和状态的离散化处理，将原混合整数最优控制模型转化成混合整数非线性规划模型；

(3)设定初始浮点数变量：在浮点数变量u(k)的可行域中随机选取一个浮点数变量带入混合整数非线性规划模型中，将模型转化成整数非线性规划模型。记u^o(k)为最优浮点数变量；

(4)格雷编码：利用格雷码对整数决策变量进行编码；

(5)建立初始自旋矩阵种群：建立由P个自旋矩阵W所组成的自旋矩阵种群，每个矩阵都代表着一个整数决策变量集，种群中的第z个个体记为W^z；

(6)种群变异：从N个变异算子中随机选取一个对自旋矩阵种群执行变异操作，得到新的自旋矩阵种群；

(7)提供扰动：利用原矩阵种群中的个体W^z和变异矩阵种群中的个体W^z′计算得到动能项的增量ΔHkin。利用动能项的增量ΔHkin计算哈密尔顿函数式差值ΔH＝(ΔJ/P)+δΔHkin；

(8)选择：满足集合Ω＝{ΔJ≤0，ΔH≤0，exp(-ΔH/T)＞random(0，1)}中任意一个条件，则将变异后的自旋矩阵W^z′赋值到W^z，更新相应参数；

(9)判别整数变量中止条件：判断是否满足终止条件，如果满足，结束循环，如果不满足，跳转到步骤(6)继续执行，直到得到最优整数决策变量W^o；

(10)建立初始浮点数变量种群：将最优整数决策变量W^o带入混合整数非线性规划模型，将原模型转化成一个浮点数非线性规划模型。建立规模为NP的浮点数变量种群，种群中的第i个个体在第G代记为其中D是个体所包含的维度，NP＝30D，种群初始化采用公式xj，i，0＝xj，min+randi，j(0，1)×(xj，max-xj，min)，其中xj，i，0表示第G＝0代，种群中第i个个体，第j个维度的值；

(11)参数和种群变异：针对两个种群的控制参数和种群，对缩放因子进行自调整。对种群采用DE/current-to-pbest/1的差分变异策略；

(12)计算适应度函数：将各个控制策略代入非线性规划模型，以性能指标作为适应度函数值；

(13)选择：将每个种群的各个控制策略相应的适应度函数作比较，保留适应度函数最小的控制参数和种群个体存入相应库中，更新相应参数；

(14)判别浮点数变量中止条件：判断是否满足终止条件，如果满足，结束循环，如果不满足，跳转到步骤(11)继续执行，直到得到当前最优浮点数变量u(k)为止，更新u^o(k)；

(15)交互式迭代搜索：将u(k)带入原混合整数非线性规划模型，将其转化成整数非线性规划模型。跳转到步骤(5)；

(16)判别局部最优解条件：判断所得最优浮点数变量是否等于u^o(k)，如果不满足，跳转到步骤(15)，如果满足，说明W^o和u^o(k)即为一个局部最优解，记录W^o和u^o(k)；

(17)判别终止条件：判断是否满足终止条件，如果满足，结束循环，如果不满足，更新u^o(k)，跳转到步骤(3)，进行全局最优解搜索，直到得到最优控制策略结束循环为止。