一种基于凸优化的高精度定位方法与流程

本发明涉及一种水下目标定位问题中的基于凸优化的高精度定位方法。

背景技术：

水声定位技术够提供海底勘查设备如ROV和AUV等重要的定位、导航和通信支撑。通过在水面工作船只、水下移动平台以及作业海区上加装和布放声学定位设备，可实现对水下目标位置的实时监控、水面与水下平台的信息交互，是海洋科学考察、海洋资源勘探、海洋资源开发、深海空间站建设等工程的必备手段。

到目前为止，水声定位技术可以分为基于测距的定位技术和不基于测距的定位技术两大类，而高精度定位技术都是通过测距方式实现的，待定位目标首先与周围信标进行通信，获得到至少四个参考信标的距离，结合已知的参考信标的位置，进行定位解算得到目标位置。在水下目标的定位解算方法中，最小二乘法具有高精度、低复杂度的优点，应用最为广泛。但是由于基于球面交汇的定位解算方程是非线性的，并且是严格非凸的，现有的方法很难得到定位问题直接最小二乘结构的全局最优解。目前常用的计算方法是通过距离方程两两相减消项去掉二次项，再利用线性最小二乘求解方法进行位置解算。但是由于这种方法消掉了二次项，定位解算结果并不是最优的。因此对于高精度水下定位技术而言有必要研究定位问题最小二乘结构的直接解算方法。

技术实现要素：

本发明的目的在于针对水声定位技术定位问题中球面交汇定位方程的最小二乘结构的一般解算方式是通过定位方程两两相减消项的方式得到线性最小二乘结构实现的，去掉二次项造成定位精度下降的问题，提出了一种提高了球面交汇定位方程的定位解算精度的基于凸优化的高精度定位方法。

本发明的目的是这样实现的：

一种基于凸优化的高精度定位方法，包括如下步骤：

(一)设目标的待解算坐标为x＝[x0,y0,z0]^T，目标首先测得到周围n个信标的距离ri和对应信标的坐标ai＝[xi,yi,zi]^T，设到每个信标的测距误差为εi，服从高斯分布εi～N(0,σi²)，得到目标的测距方程为：

ri＝||x-ai||+εi,i＝1,2,...,n

根据距离测量残差平方和最小的原则建立球面交汇定位问题的最小二乘结构：

(二)步骤(一)求出的最小二乘结构展开，去掉常数项得：

F(x)＝f(x)-g(x)

其中

(三)约束条件设置方面，由于目标的测距误差服从高斯分布，根据高斯分布的3σ准则，令δi＝3σi得到：

||xk-ai||≤ri+δi

ri-δi≤||xk-ai||

得到带约束条件的优化方程

(四)对步骤(三)中得到的优化方程的目标函数和限制条件进行仿射近似，转化为可以利用凸优化求解的方程形式，形式如下：

subject to fi(x)-gi(x)≤0,i＝1,...,m,

其中x∈Rⁿ，并且fi:Rⁿ→R,gi:Rⁿ→R,(i＝0,...,m)都是凸函数；

根据泰勒公式对定位方程中的非凸的gi(x)进行仿射近似；

对目标函数进行仿射近似可得：

对非凸的约束条件进行仿射近似可得：

||x-ai||-ri-δi≤0

从而得到关于定位问题可以利用凸优化求局部解的最优化方程：

s.t:||x-ai||-ri-δi≤0

(五)在限制条件中添加松弛变量扩大可行域，并结合在目标函数中添加罚函数的方法放宽对初始目标位置的限制；

(5.1)对原方程添加松弛变量si和以及惩罚函数得到转化后的优化方程：

subject to:||x-ai||-ri-δi≤si

(5.2)设定位置初值x0，迭代最大次数Kmax，初始惩罚因子τ0，惩罚因子增长系数μ＞0，设置迭代次数为k＝0；

(5.3)利用凸优化工具包求解步骤一中添加松弛变量和罚函数的优化方程解出变量x^*,s^*,

(5.4)更新惩罚因子τk+1＝μτk,k＝k+1；

(5.5)如果迭代次数达到上限，终止迭代，将最终的x^*作为最终结果，否则继续转到步骤(5.3)进行迭代。

本发明的有益效果在于：通过将水下目标球面交汇定位方程的最小二乘结构进行形式变换并添加限制条件，将其转化为凸优化理论中的DC结构的形式，进而可以利用凸-凹过程(CCP)的方法来求解，并针对直接CCP算法需要迭代初值在可行域内的缺点在原优化方程添加松弛变量和罚函数，扩大可行域，放宽对初值的限制。较线性最小二乘定位解算方法而言可以提高定位精度，实现高精度水下目标定位。

附图说明

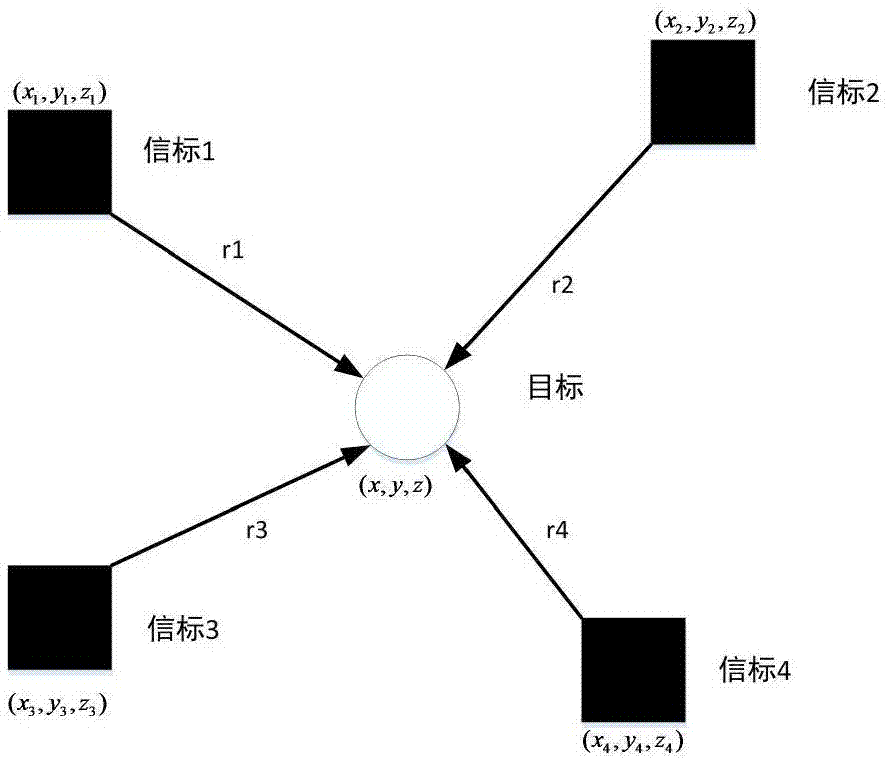
图1为本发明目标与通信范围内的信标通信示意图；

图2为本发明添加松弛变量和罚函数后凸-凹过程求解定位方程的流程图；

图3为本发明仿真添加松弛变量和罚函数的凸-凹过程定位误差与线性最小二乘定位误差的对比图；

图4为本发明图3中200-300次仿真结果的局部放大图。

图5为本发明图3中300-450次仿真结果的局部放大图。

具体实施方式

下面结合附图对本发明做进一步的说明。

实现本发明的基本思想是，通过将球面交汇定位方程的最小二乘结构形式变换、添加限制条件，将其转化为凸优化问题中的DC(difference of convex)结构形式，再将目标函数和限制条件进行仿射近似，转化为可以用凸优化方法求解的非线性优化问题，可以利用凸优化理论中的凸-凹过程(CCP)方法求出变换后定位方程最小二乘结构的局部解。但是，凸-凹过程迭代求解方法具有要求迭代初始点必须是可行域内的点的缺点，通过在原有CCP方法上添加松弛变量和罚函数的罚凸-凹过程(PCCP)方法，可以放宽对初值的限制、提高算法的适用性。

本发明的具体实施步骤如下：

步骤一：测量到信标的距离、建立定位问题的最小二乘结构模型。

假设目标的待解算坐标为x＝[x0,y0,z0]^T，目标首先测得到周围n个信标的距离ri和对应信标的坐标ai＝[xi,yi,zi]^T。设到每个信标的测距误差为εi(服从高斯分布εi～N(0,σi²))，则得到目标的测距方程为：

ri＝||x-ai||+εi,i＝1,2,...,n (1)

根据距离残差平方和最小的原则建立球面交汇定位问题的最小二乘结构：

步骤二：对步骤一步求出的最小二乘结构进行变换。步骤一步求出的最小二乘结构展开，去掉常数项得：

F(x)＝f(x)-g(x) (3)

其中

步骤三：添加限制条件。

约束条件设置方面，由于目标的测距误差服从高斯分布，根据高斯分布的3σ准则，令δi＝3σi得到：

得到带约束条件的优化方程

步骤四：对步骤三中得到的优化方程的目标函数和限制条件进行仿射近似，转化为可以利用凸优化求解的方程形式。

凸优化理论中有一类DC问题，其一般形式如下：

其中x∈Rⁿ，并且fi:Rⁿ→R,gi:Rⁿ→R,(i＝0,...,m)都是凸函数。可见步骤二中对定位问题最小二乘结构进行整理得到的带约束条件的优化方程符合DC问题的一般形式。由于DC(Differ ence of convex programming)问题中只有gi(x)是仿射函数的条件下，才是凸优化问题，才能利用凸优化方法求其局部解。所以首先要根据泰勒公式对定位方程中的非凸的gi(x)进行仿射近似。

对目标函数进行仿射近似可得：

对非凸的约束条件进行仿射近似可得：

从而得到关于定位问题可以利用凸优化求局部解的最优化方程：

步骤五：对步骤四中得到的优化方程添加惩罚函数和松弛变量，放宽凸优化求解转换之后优化方程凸优化求解迭代初始目标位的置限制。

步骤四中将原定位问题的最小二乘结构经变换和仿射近似之后得到的最优化方程可以利用Yuille和Rangarajan在2003年提出的凸-凹过程(CCP)方法来求解，但是凸-凹过程求解仿射近似后的DC问题要求迭代初始点x0必须在可行域内，实际情况下有可能很难得到可行域内的点。在限制条件中添加松弛变量扩大可行域，并结合在目标函数中添加罚函数的方法可以放宽对初始目标位置的限制。具体步骤如下：

(1)对原方程添加松弛变量si和以及惩罚函数得到转化后的优化方程：

(2)设定位置初值x0，迭代最大次数Kmax，初始惩罚因子τ0，惩罚因子增长系数μ＞0，设置迭代次数为k＝0

(3)利用凸优化工具包求解步骤一中添加松弛变量和罚函数的优化方程解出变量x^*,s^*,

(4)更新惩罚因子τk+1＝μτk,k＝k+1

(5)如果迭代次数达到上限，终止迭代，将最终的x^*作为最终结果，否则继续转到步骤(3)进行迭代；

具体为：

步骤一：测量到信标的距离、建立定位问题的最小二乘结构模型。

参照图1，设待求解目标位置为x＝[x0,y0,z0]^T目标首先与通信范围内的信标(本实例设置信标数量为4)进行通信，获得各个信标的位置坐标ai＝[xi,yi,zi]^T和到各信标的距离ri。得到目标到各信标的测距方程：

ri＝||x-ai||+εi,i＝1,2,...,n (1)

根据距离测量残差平方和最小的原则建立球面交汇定位问题的最小二乘结构：

步骤二：对步骤一步求出的最小二乘结构进行变换

将步骤一中的定位问题的最小二乘结构展开可得：

去掉常数项则应有：

令可得F(x)＝f(x)-g(x)。

步骤三：添加限制条件。

添加限制条件方面，由于测距误差服从高斯分布，根据高斯分布的3σ准则令δi＝3σi应有，故限制条件设置为：

得到带约束条件的优化方程

步骤四：对步骤三中得到的优化方程的目标函数和限制条件进行仿射近似，转化为可以利用凸优化求解的方程形式。

凸优化理论中有一类DC问题，其一般形式如下：

其中x∈Rⁿ，并且fi:Rⁿ→R,gi:Rⁿ→R,(i＝0,...,m)都是凸函数。可见步骤二中对定位问题最小二乘结构进行整理得到的带约束条件的优化方程符合DC问题的一般形式。由于DC(Differ ence of convex programming)问题中只有gi(x)是仿射函数的条件下，才是凸优化问题，才能利用凸优化方法求其局部解。所以首先要根据泰勒公式对定位方程中的非凸的gi(x)进行仿射近似。定位方程中gi(x)在展开点xk进行仿射近似的方法为：

对目标函数进行仿射近似并去掉常数项可得：

对非凸的约束条件进行仿射近似可得：

从而得到关于定位问题可以利用凸优化求局部解的最优化方程：

步骤五：对步骤四中得到的优化方程添加惩罚函数和松弛变量，放宽凸优化求解转换之后优化方程凸优化求解迭代初始目标位置的限制。

步骤四中将原定位问题的最小二乘结构经变换和仿射近似之后得到的最优化方程可以利用Yuille和Rangarajan在2003年提出的凸-凹过程(CCP)方法来求解，但是凸-凹过程求解仿射近似后的DC问题要求迭代初始点x0必须在可行域内，实际情况下有可能很难得到可行域内的点。在限制条件中添加松弛变量扩大可行域，并结合在目标函数中添加罚函数的方法可以放宽对初始目标位置的限制。参照图2，具体步骤如下：

(1)对原方程添加松弛变量si和以及惩罚函数得到转化后的优化方程：

(2)设定位置初值x0，迭代最大次数Kmax，初始惩罚因子τ0，惩罚因子最大值τmax，惩罚因子增长系数μ＞0，设置迭代次数为k＝0

(3)利用凸优化工具包求解步骤一中添加松弛变量和罚函数的优化方程解出变量x^*,s^*,

(4)更新惩罚因子τk+1＝min(μτk,τmax),k＝k+1

(5)如果迭代次数达到上限，终止迭代，将最终的x^*作为最终结果，否则继续转到步骤(3)进行迭代；

本发明方法的仿真分析：

(1)设置水下4个信标随机布放在150×150×150的三维区域中，目标位置为100×100×100区域内的随机点。

(2)设置水下目标到信标之间的测距误差服从为均值为0标准差为0.1的高斯分布

(3)令线性最小二乘定位结果作为添加松弛变量和罚函数的CCP算法的迭代初值，迭代最大次数Kmax设置为20，初始惩罚因子τ0设置为1，惩罚因子增长系数μ设置为3。

(4)进行500次仿真，统计添加松弛变量和罚函数的CCP算法(PCCP)的定位误差和线性最小二乘算法的定位误差以及各自的平均定位误差。

500次仿真后线性最小二乘结构常规解法平均定位误差为2.0601；添加松弛变量和罚函数的CCP算法(PCCP)解法平均定位误差为0.6914，以步长为50选取第1-500次仿真中线性最小二乘方法定位误差与PCCP算法定位误差的对比结果如下表所示：

附图3中为500次仿真后，添加松弛变量和罚函数的CCP算法的定位误差和线性最小二乘算法的定位误差的对比图。附图4、5是附图3的局部放大图。

可以看出添加松弛变量和罚函数的CCP算法的定位误差基本上均小于线性最小二乘算法的定位误差。说明添加松弛变量和罚函数的CCP算法能通过直接求解球面交汇定位方程的最小二乘结构的方式提高定位精度，达到实现高精度定位解算的目的。