一种工业控制多回路振荡行为稀疏因果分析方法与流程

本发明涉及工业控制中的故障诊断领域，具体涉及一种工业控制多回路振荡行为稀疏因果分析方法。

背景技术：

工业常见的化工过程有成千上万个高度耦合的回路组成，且过程设备具有规模大，变量多，综合度高，且长时间运行在闭环控制下等特点。但是，由于控制回路中控制器的过整定、过程的非线性、阀门粘滞和外部扰动等原因，控制回路会出现振荡，甚至是控制回路的全局振荡，这极大地影响了工业流程设备运行稳定性和生产效益。

对工业过程的振荡回路进行因果分析，包括振荡源的检测和传播路径的分析，是振荡诊断和分析的重要组成部分，有利于提高产品的合格率，增强工业流程设备运行过程中的可靠性、安全性，提高生产效益。由于外部干扰因素或设备自身问题的影响，控制器的性能会逐渐降低甚至失效，某些控制回路会出现振荡，甚至出现全局振荡。因此，在工业控制系统故障诊断过程中，针对振荡回路设计有效的因果分析方法，及时、准确的确定振荡源和振荡传播路径，对于控制回路故障诊断具有重要意义。

现有的工业控制回路振荡行为的分析方法，大部分是针对振荡的检测，并没有涉及振荡回路关系的分析。最近十年，有出现基于工业过程原理和控制方案的振荡行为因果分析方法，或者基于谱主成分分析的方法对振荡源进行定位的方法，也有利用格兰杰因果分析方向实现对振荡回路的因果分析。

但是上述方法的局限性体现在：基于原理的分析方法普适性差，分析效率低；而基于谱主成分分析的方法只能确定振荡源，无法获知振荡的传播路径；而单一仅利用格兰杰因果分析，因回路众多且强耦合，算法计算效率低，计算结果复杂，而振荡回路的数据中的余弦趋势，使得回路之间存在高度的相似性和重复性，影响最终分析结果的准确性。

因而，在工业过程振荡行为的因果分析中，对振荡回路的数据进行有效的预处理，实现对振荡源的准确快速定位及传播路径的建模，对于工业过程振荡行为分析有非常重要的意义，也有利于工业过程故障的诊断和排除。

技术实现要素：

本发明提供一种工业控制多回路振荡行为稀疏因果分析方法，适用于多个振荡回路中振荡源的检测和振荡传播路径的分析，检测方法适用于分析多振荡回路的振荡数据，只需获取振荡行为发生时的数据，无需过程机理知识。

一种工业控制多回路振荡行为稀疏因果分析方法，包括：

步骤1，采集各个待分析的控制回路的过程输出时间序列信号；

步骤2，对各个过程输出时间序列信号进行去余弦趋势预处理，得到相应的子信号；

步骤3，对各个控制回路的子信号建立稀疏多变量向量自回归模型；

步骤4，基于稀疏多变量自回归模型进行格兰杰因果分析，得到任意两个控制回路间的格兰杰因果指标；

步骤5，对格兰杰因果指标进行统计显著性判断，若结果显著，则认为在相应显著水平下，该格兰杰因果指标表示的相应控制回路间的因果关系成立。

通过对待分析的振荡回路数据过程输出时间序列信号进行去余弦趋势预处理，建立稀疏向量自回归模型，并在模型基础上进行回路间的格兰杰因果分析，计算格兰杰因果指标，最后进行统计显著性判断，实现对该工业过程振荡行为的稀疏因果分析，实现振荡源的定位和振荡传播路径的检测。

本发明采用化工过程的可测变量作为过程输出时间序列信号，振荡回路数据经现场采集后，进行快速有效的分析，完成振荡源定位和传播路径建模，实现振荡故障的快速诊断和排除。

本发明首先对振荡回路数据进行预处理，去除余弦趋势，利用线性LASSO拟合的方法，完成多变量稀疏向量自回归模型建模，在模型基础上，选择回路进行格兰杰因果分析，计算格兰杰因果指标，最后进行统计显著性检验，判断指标所表示的回路间的因果关系是否成立。

本发明中的对变量稀疏向量自回归模型由线性LASSO拟合得到，模型系数矩阵具有稀疏的特点，大幅度减少了需要进行格兰杰因果分析的回路对，提高算法效率，实现了多回路振荡行为的因果分析。

作为优选，步骤2中的去余弦趋势预处理具体包括：

步骤2-1，若待分析的控制回路的振荡周期已知，则直接执行步骤2-2；若待分析的控制回路的振荡周期未知，则对其过程输出时间序列信号进行分解，提取振荡子信号以得到所述待分析的控制回路的振荡周期，再执行步骤2-2；

步骤2-2，采用滑动均值法对所述过程输出时间序列信号进行分解即完成去除余弦趋势预处理，采用滑动均值法进行分解时采用的滑动均值窗口长度等于振荡周期。

本发明中优选采用本质时间尺度分解、局部均值分解中的一种方法对过程输出时间序列信号进行分解。

步骤2-1中，振荡周期未知时，提取每个控制回路的振荡子信号，并且需要满足下述检验，否则需要重新提取。

检验方法：求取每个控制回路振荡的子信号的自相关函数，并计算自相关函数的相邻极大值点的滞后阶数的差值序列，该差值序列需满足以序列中位数为基础，差值序列中各个元素与该序列中位数相比波动不超过±5％，则以该差值序列的序列中位数作为该回路的振荡周期，并通过检验。若不满足要求，则重新提取振荡子信号。

最后，求取所有回路的振荡周期序列的中位数，作为去余弦趋势的滑动均值窗口值。

步骤3中，针对每个待分析的控制回路采用LASSO拟合方法建立稀疏多变量向量自回归模型。

其中第i个控制回路的多变量自回归模型如下：

其中，i为回路标号，i＝1,2,…K，K为待分析的控制回路总数；x_i(t)为第i个控制回路过程信号t时刻的采样值；τ为滞后期数，τ＝p_start(i),p_start(i)+1,…p_end(i)；a_iτ为第i个控制回路滞后期数τ时的回归系数。

作为优选，步骤3中，针对每个待分析的控制回路采用线性LASSO拟合方法建立稀疏多变量向量自回归模型。

线性LASSO拟合方法及参数设置如下：

其中，y为N×1维因变量矩阵，y矩阵均值为1方差为0，X为N×K维自变量矩阵，X矩阵列向量均值为1方差为0，A为K×1维系数矩阵，为向量·的2-范数平方值，||·||₁为向量·的1-范数，λ∈(0,1)，λ的具体取值由10折交叉验证确定，取拟合残差均方最小值加一个标准误时对应的λ值。

步骤3中，针对任意一个待分析的控制回路采用线性LASSO拟合方法建立稀疏多变量向量自回归模型时具体步骤如下：

步骤3-1，根据BIC最小原则，依次确定当前待分析的控制回路的最大滞后期数和开始滞后期数；

步骤3-2，根据所述的最大滞后期数和开始滞后期数对当前待分析的控制回路进行线性LASSO拟合，即求解得到稀疏向量自回归模型。

步骤3-1中，首先根据BIC最小原则，确定第i个控制回路的最大滞后期数p_end(i)，

其中，Σ为残差协方差阵，T为回归计算时间序列信号长度，K为回路总个数，p为滞后期数，从1开始取值，逐一增加至p_max，p_max>1，一般可根据实际情况进行设置；

然后根据计算得到的最大滞后期数p_end(i)，再根据BIC最小原则，确定第i个控制回路的开始滞后期数p_start(i)，

p_start(i)＝p_end(i)-m0+1，

其中，p_end(i)为最大滞后期数，m0为BIC最小原则确定的总滞后期数m值，Σ为残差协方差阵，T为回归计算时时间序列信号长度，K为回路总个数，m为总滞后期数，m从1开始取值，逐一增加，最大值为p_end(i)。

步骤4中，根据各个控制回路的稀疏多变量向量自回归模型确定任意两个控制回路之间的相关性，并针对任意两个确定相关的控制回路进行格兰杰因果分析得到该相关的两个控制回路之间的格兰杰因果指标。

基于稀疏多变量自回归模型进行格兰杰因果分析，得到任意两个控制回路间的格兰杰因果指标，通过计算任意两个控制回路之间的格兰杰因果指标，实际上得到一个针对所有待分析控制回路的格兰杰因果指标方阵G，G为K×K方阵，K为待分析的控制回路的总数，坐标为(i,j)处的元素G(i,j)表示第i个控制回路为结果，第j个控制回路为原因时的格兰杰因果指标。

其中，计算第i个控制回路的格兰杰因果指标的具体方法如下：

步骤4-1，根据第i个控制回路的稀疏多变量向量自回归模型，进行如下判断：

若满足条件1：则则认为第j个控制回路与第i个控制回路不存在因果关系；

若满足条件2：则表示第j个控制回路与第i个控制回路可能存在因果关系，并执行步骤4-2计算格兰杰因果指标；

其中，p_start(i)为第i个控制回路的开始滞后期数，p_end(i)为第i个控制回路的最大滞后期数，a_jτ为第j个控制回路滞后期数τ时的回归系数，m＝1,2……K；

步骤4-2，计算满足条件2的控制回路和与其相关的各个控制回路之间的格兰杰因果指标，其中第i个控制回路为结果，第j个控制回路为原因的格兰杰因果指标G(i,j)：

其中，为除第j个控制回路时间序列信号之外，满足条件2的其他所有回路信号对第i个控制回路进行最小二乘拟合的残差协方差矩阵行列式的值；|∑e|为满足条件2的所有回路信号对第i个控制回路进行最小二乘拟合的残差协方差矩阵行列式的值。

作为优选，统计显著性检验方法如下：

步骤5-1，计算每个格兰杰因果指标对应的p_值；

步骤5-2，若该格兰杰因果指标对应的p_值小于预设的置信水平，则认为该格兰杰因果指标表示的因果关系成立；否则，认为该格兰杰因果指标表示的因果关系不成立。

作为优选，所述步骤5-2中预设的置信水平为0.005～0.01。进一步优选，所述置信水平为0.005或0.01。

计算每个格兰杰因果指标对应的p_值时采用文献R语言与统计分析[J].2008第81页例子中公开的方法计算。

本发明与现有技术相比具有的有益效果：

1、算法仅利用发生振荡行为的回路数据，无需外部附加的信号激励，实现非侵入式的检测与诊断；

2、数据采用数据驱动型的方法，无需过程先验知识，无需预先设计滤波器，也不需进行人工干预。

3、算法原理简单，易于编写，便于操作；

4、采用LASSO拟合方式，实现多变量自回归模型的稀疏建模，降低格兰杰因果分析的工作量，提高分析效率；

5、对原始数据采取去余弦趋势的预处理方法，利用过程数据的随机噪声进行因果分析，分析结果更加准确有效。

6、算法的计算结果，不仅可以实现对振荡源的定位，也实现了对振荡传播路径的建模分析，为故障的排查和诊断提供可靠的依据。

附图说明

图1为本实施例中的TE过程的流程及控制方法示意图；

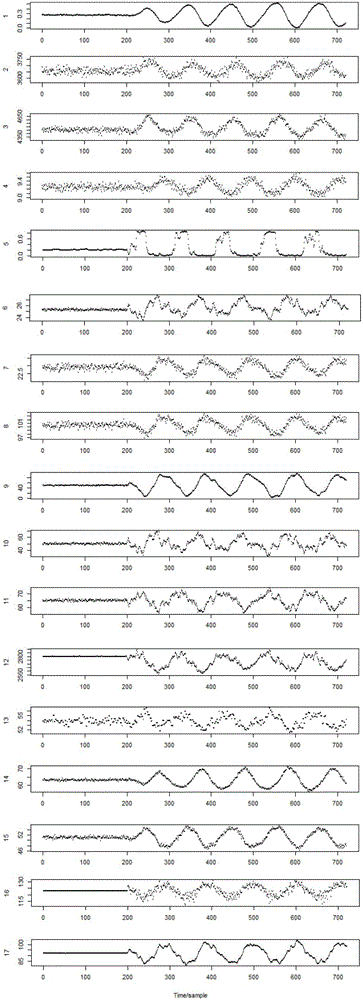
图2为本实施例中采集的TE过程多振荡回路中输出信号图，从下至上依次为第1个控制回路到第17个控制回路；

图3为本实施例的工业控制多回路振荡行为稀疏因果分析方法的流程图；

图4为本实施例中稀疏因果分析结果图。

具体实施方式

下面以基于TE过程(Tennesee-Eastman Process)的振荡行为为例，对存在振荡行为的化工过程的稀疏因果分析方法做详细描述。

本实施例中TE过程的控制方案采用分散控制方案，如图1所示，依据“Ricker N L.Decentralized Control of the Tennessee Eastman Challenge Process[J].Journal of Process Control,1996,6(4):205-221.”。

TE过程最早由Eastman化工公司的工程师Downs和Vogel在实际工业流程的基础上修改提出的，具有过程各回路强耦合、高度非线性且开环不稳定等特性。

TE过程的化学反应如下：

A(气)+C(气)+D(气)→G(液)

A(气)+C(气)+E(气)→H(液)

A(气)+E(气)→F(液)

3D(气)→F(液)

有四种反应物A，C，D和E以及两种产物G和H，另外B是惰性组分，F为副产物。所有的反应都是不可逆放热反应，反应速度由温度和反应物气象浓度决定。

设备有冷凝器、压缩机、分离器、汽提塔五个单元，四种进料流，一个产品流和一个废气流，12个执行器，其中11个为执行阀，还有一个是反应器中的搅拌器。图中RCL1、RCL2、RCL3、RCL4、RCL5、RCL6、RCL7、FCL8、LCL9、LCL10、LCL11、PCL12、XCL13、XCL14、XCL15、XCL16和TCL17分别为本实施例的待分析的17个控制回路(即回路)的控制器。图中V1、V2、V3、V4、V6、V7、V8、V10、V11分别为控制回路中的控制阀门。

TE过程各设备及反应过程参数设置，依据“Downs J J,Vogel E F.A plant-wide industrial process control problem[J].Computers Chemical Engineering,1993,17(3):245-55.”实施。

TE过程采样时间0.1小时(360秒)，运行时间为72小时，考虑如表1所示的17个控制回路用于振荡行为的因果分析。

表1

在TE过程稳定运行2小时后，在回路16加入振荡扰动，已知振荡为105个采样点/周期，采集到如图2所示的回路信号图(即该回路的过程输出时间序列信号图)，图2横坐标为采样点序数，单位为sample(1个sample对应一个数据达到采样间隔)，纵坐标为各个控制回路变量的单位。

如图3所示，本实施例的工业控制多回路振荡行为稀疏因果分析方法，包括：

步骤1，采集如上17个控制回路的过程输出时间序列信号。

采集过程输出时间序列信号的方法为，在预设的每个采样间隔内记录下待检测振荡回路的过程数据，且每个采样间隔内采集到的过程数据添加在先前采集的数据末端。

采样间隔一般与工业控制系统中的控制周期相同，也可以选择为控制周期的整数倍，具体根据性能监控和工业现场的实时性要求和数据存储量限制来确定。

本实例中，回路振荡行为的发生由人工添加振荡扰动产生，为更好模拟实际工业过程情况，采用2.5小时到72小时的过程输出时间序列信号作为待分析的回路数据，即数据不包含振荡的起始时刻的信号。

步骤2，对采集到的过程输出信号(即过程输出时间序列信号)进行去余弦趋势的预处理。

由于过程输出信号的原始数据存在相同的余弦趋势，不同回路(即控制回路)之间存在高度相似性，经标准差标准化后，不同回路数据可以通过时间轴平移实现相互拟合与重复，从而导致格兰杰因果分析结果的错误。而回路信号中包含的有色噪声信号，只有原因回路对结果回路实现拟合与预测，反之则不可行。因而，原始数据(即过程输出时间序列信号)经过去余弦趋势后，才适用于格兰杰因果分析。

本实施例中，回路的振荡周期已知为105个采样点。若回路的振荡周期未知，本发明建议使用本质时间尺度分解、局部均值分解中的一种方法对过程输出时间序列信号进行分解，求取得到回路的振荡周期。

本质时间尺度分解可依据现有技术“Frei M G,Osorio I.Intrinsic time-scale decomposition:time–frequency–energy analysis and real-time filtering of non-stationary signals[J].Proceedings of the Royal Society A:Mathematical,Physical and Engineering Science,2007,463(2078):321-342.”实施。

局部均值分解可依据现有技术“Smith J S.The local mean decomposition and its application to EEG perception data[J].Journal of the Royal Society Interface,2005,2(5):443-454.”实施。

在本实施例中，直接以105作为滑动滤波的窗口值。本实施例中，滑动滤波去余弦趋势优选使用R{stats}函数包中的decompose函数实现。余弦趋势即为该函数输出中的seasonal项，用原始信号减去该项即可完成去余弦趋势预处理得到相应的子信号。

步骤3，对子信号建立稀疏多变量向量自回归模型。

稀疏多变量向量自回归模型的建立是准确高效进行后续因果分析的关键。本实施例中，采用线性LASSO拟合方法对经预处理的回路过程时间序列信号建立稀疏多变量向量自回归模型，模型如下：

其中，i为回路标号，i＝1,2,…K，共有K个控制回路(本实施例中K＝17)；x_i(t)为第i个控制回路过程信号t时刻的采样值；τ为滞后期数，τ＝p_start(i),p_start(i)+1,…p_end(i)；a_iτ为第i个控制回路滞后期数τ时的回归系数。

线性LASSO拟合方法及参数设置如下：

其中，y为N×1维因变量矩阵，y矩阵均值为1方差为0，X为N×K维自变量矩阵，X矩阵列向量均值为1方差为0，A为K×1维系数矩阵，表示求向量·的2-范数平方值，||·||₁表示求向量·的1-范数，λ∈(0,1)。

线性LASSO拟合可以通过调整惩罚系数λ的值，实现拟合结果的稀疏，即拟合系数中多数为0。所以选取合适的λ值，可以实现变量关系的精简，防止出现过拟合，又可以提取有效的变量关系，实现稀疏多变量向量自回归模型的建模。为达到上述目的，λ的具体取值由10折交叉验证确定，取拟合残差均方最小值加一个标准误时对应的λ值。

稀疏多变量模型的建立具体步骤如下：

步骤3-1，根据BIC最小原则，确定第i个控制回路的最大滞后期数p_end(i)，

其中，Σ为残差协方差阵，T为回归计算时时间序列信号长度，K为回路总个数，p为滞后期数，从1开始取值，逐一增加至p_max，本实施例中设置p_max＝4，

步骤3-2，根据BIC最小原则，确定第i个控制回路开始滞后期数p_start(i)，

p_start(i)＝p_end(i)-m0+1，

其中，p_end(i)为步骤4-1确定的最大滞后期数，m0为BIC最小原则确定的总滞后期数m值，Σ为残差协方差阵，T为回归计算时时间序列信号长度，K为回路总个数，m为总滞后期数，m从1开始取值，逐一增加，最大值为p_end(i)；

本实施例中，最终确定的模型(即稀疏多变量向量自回归模型)滞后期数为：

(p_start(i),p_end(i))＝(1,1)(i＝1,2…16,17)。

步骤3-3，根据步骤3-1和步骤3-2确定的稀疏向量自回归模型滞后期数(p_start(i),p_end(i))对第i个控制回路进行拟合，求解各个控制回路的稀疏对变量向量自回归模型。以第一个回路为例进行说明，第1个控制回路的模型为：

x₁(t)＝0.938x₁(t-1)-0.138x₁₄(t-1)。

其中，x₁(t)表示t采样时刻回路1的值，x₁(t-1)、x₁₄(t-1)表示t-1采样时刻回路1、14的值。

步骤4，基于各个控制回路的稀疏多变量向量自回归模型，进行格兰杰因果分析，并计算该TE过程的格兰杰因果指标方阵G，G为K×K方阵，坐标为(i,j)处的元素G(i,j)表示第i个控制回路为结果，第j个控制回路为原因时的格兰杰因果指标。本实施例中，i＝1,2……K，j＝1,2……K，K＝17。具体方法如下：

步骤4-1，根据第i个回路建立的稀疏多变量向量自回归模型，

对回路进行分类

若满足类1条件，则认为第j个控制回路与第i个控制回路不存在因果关系，无需进行格兰杰因果分析及系数的计算，并直接令G(i,j)＝0；

若满足类2条件，则认为表示第j个控制回路与第i个控制回路可能存在因果关系，需要执行步骤4-2计算格兰杰因果指标；

步骤4-2，计算满足类2条件回路的格兰杰因果指标。格兰杰因果原理参照可以参照“Granger C W J.Investigating causal relations by econometric models and cross-spectral methods[J].Econometrica,1969,37(3):424-38.”。本发明中，具体实施方法如下：

其中，为除第j个控制回路的过程输出时间序列信号之外，且满足类2条件的其他所有回路信号对第i个控制回路进行最小二乘拟合的残差协方差矩阵行列式的值；|∑e|为满足类2条件的所有回路信号对第i个控制回路进行最小二乘拟合的残差协方差矩阵行列式的值。

步骤5，对格兰杰因果指标，进行统计显著性检验。

为了更加准确判断变量间的因果关系，对本实施例的格兰杰因果指标矩阵进行统计显著性检验，原理如下：

(T-p(i))G(i,j)～χ²(p(i))，p(i)＝p_end(i)-p_start(i)+1

i,j＝1,2…17

H0：第i个控制回路为结果，第j个控制回路是原因的因果关系不成立；

H1：第i个控制回路为结果，第j个控制回路是原因的因果关系成立。

显著性检验的具体步骤如下：

步骤5-1，逐一计算格兰杰因果指标方阵G中每个元素对应的p_值；

步骤5-2，本实施例中，设置置信水平α为0.001；

步骤5-3，若坐标(i,j)处元素的p_值小于显著水平α，则拒绝H0，即接受H1，反之，则接受H0。

坐标(i,j)处元素的p_值参照汤银才在书本R语言与统计分析[J].2008.第81页例子，利用R语言中的pchisq函数可以实现p_值计算，根据已知(i,j)处的对应的G(i,j)值、第i个回路的阶次p(i)值，时间序列信号长度T即可完成计算。

绘制满足统计显著性的格兰杰因果指标的关系图，如图4所示，“i→j”表示回路i是原因回路j结果的因果关系成立，i、j为回路标号。本实施例中回路振荡行为的稀疏因果分析结果表明，可以正确判断回路16为振荡源，且因果关系图中表示的振荡传播路径符合TE过程的原理和实际控制方案。

利用本发明方法，对于工业控制多回路振荡行为，实现了振荡源的定位和振荡传播路径的检测，为振荡故障的诊断和排查提供了丰富的数据支持，提高了诊断排查的效率。