基于区间二型T-S模型的网络化控制系统的鲁棒容错控制方法与流程

本发明涉及基于容错控制的网络控制设计领域，特别地涉及一种基于区间二型t-s模型的网络化控制系统的鲁棒容错控制方法。

背景技术：

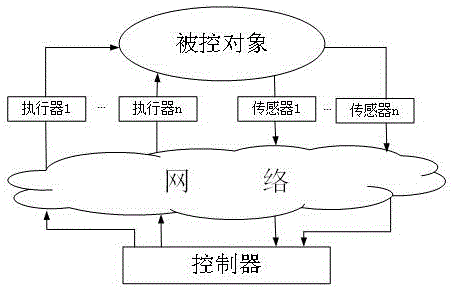
网络化控制系统(ncs)是通过网络连接被控对象、传感器、执行器、控制器而形成的一个闭环控制系统，图1即为网络化控制系统的结构框图。与传统的点对点方式连接的控制系统相比，ncs具有成本低、连线少、便于系统的维护、安装等优点。然而由于数据需要在网络中传递，无法避免的会有一些问题产生，比如网络诱导时滞、数据丢包、时序错乱以及网络调度。

此外，ncs规模越来越庞大、结构复杂、不确定因素众多，一旦系统中的某部分发生故障，而造成的损失难以估计。因此，具有较强容错能力的ncs已经成为现代ncs的性能要求。近年来，ncs的容错控制的研究也越来越来受到广泛的关注。

众所周知，takagi-sugeno(t-s)模糊系统在过去的几十年间已经被广泛得使用在工业应用当中。自从1965年zadeh教授创立了描述模糊现象方法的模糊集合论以来，模糊系统引起了很多领域众多的研究者的兴趣。zadeh教授在1975年提出了二型模糊集合理论，之后其他学者进一步提出了区间二型模糊集合的概念，区间二型模糊模型在解决非线性系统和含有不确定信息的系统中有较大的作用，其经典的应用涉及工业生产和生活的许多层面，例如在家用电器设备中有模糊洗衣机、摄录机等；在工业控制领域中有水净化处理、水泥窑炉等。

技术实现要素：

本发明针对一类具有参数不确定的非线性网络控制系统，同时考虑网络诱导时滞，基于区间二型t-s模型，在执行器发生故障时，通过构造合适的lyapunov-krasovskii泛函，引入自由权矩阵来表示newton-leibniz公式中的各项之间的关系，运用不等式放缩、矩阵分解技巧、相互凸组合、改进的詹森不等式和并行分布补(pdc)偿技术，设计了使系统渐近稳定并满足h∞性能指标的状态反馈控制器。

本发明解决技术问题所采取的技术方案为：

㈠：利用区间二型t-s模糊模型对网络控制系统建立模型，用if-then规则描述网络控制系统如下：

其中，nai是前件变量θa(x(t))(a＝1,2,…,p)在第i(i＝1,…,r)条规则下的模糊集；是系统状态向量；是控制输入向量；是干扰向量，且ω(t)∈l2[0,∞)；是输出向量；ai,b1i,b2i,ci,di是具有适当维数的常数矩阵；δai,δb1i是参数不确定性矩阵，且[δaiδb1i]＝hif(t)[eaiebi]；ηi,eai,ebi是已知矩阵，f(t)是未知矩阵，且满足f^t(t)f(t)≤i。

㈡：在不确定网络控制系统中加入隶属度函数，通过单点模糊化、乘积推理和中心平均去模糊化，上述网络控制系统的全局模型调整为：

其中，[hi^l(x(t))hi^u(x(t))]是第i条规则的激活强度；是θa(x(t))的上下隶属度，且式(2)中的hi(x(t))如下定义：

式(3)中αi(x(t))，是系统不确定相关的非线性函数，且满足

㈢：在控制器中加入执行器容错控制矩阵：

考虑执行器失效模型：

u^f(t)＝mau(t)(4)

执行器容错矩阵：mai和是一个标量。下面将给出不同执行器出现故障的情况：

⑴：如果那么mai＝0这将代表着ui^f(t)执行器完全失效。

⑵：当那么mai＝1这将代表着ui^f(t)执行器完全有效。

⑶：当这将代表着ui^f(t)执行器部分失效。

假设传感器是时间驱动、控制器和执行器是事件驱动，网络控制时延τk＝τk^sc+τk^c+τk^ca，这里的τk^c表示控制器的计算延迟时间，τk^sc表示传感器到控制器的延迟时间；τk^ca表示控制器到执行器的延迟时间。

㈣：设计网络控制系统中的状态反馈控制器，采用并行分布补偿法，模糊控制规则如下：

其中,kj(j＝1,2,…,r)为第j个控制规则的反馈增益矩阵，h是信号的采样周期，tkh是第k次的采样时刻。定义τ(t)＝t-tkh，时滞参数设置如下：hmm＝hm-hm，hm≤τ(t)≤hm。

以下在矩阵中的*号代表对称位置上元素的转置。状态反馈控制器的全局模型是：

为了简便计算：hi(x(t))＝hi,hj(x(tkh))＝hj^k。

㈤：将全局的状态反馈控制器代入到全局的网络控制系统中，得到完整的闭环网络系统：由(2)式和(6)式所确立的闭环模糊系统如下：

本发明得有益效果：

1：网络控制系统中存在非线性和较多的不确定信息，区间二型t-s模糊模型可以用局部线性系统任意精度去逼近全局非线性系统，且在处理不确定信息方面弥补了一型模糊集，其与二型模糊集相比降低计算复杂度。故选取区间二型t-s模糊为含有不确定信息的非线性网络系统建模有较大的优势。

2：考虑了现场实时情况，假设部分执行器故障的情况下，保证整个网络控制系统稳定运行，且满足抑制干扰性能指标γ。

3：在选取lyapunov-krasovskii泛函时充分考虑时滞信息，在v2(t)和v3(t)中考虑时滞上下界，并引入自由权矩阵降低了结果的保守性。

附图说明

图1网络化控制系统结构框图。

图2闭环系统状态x(1)响应曲线。

图3闭环系统状态x(2)响应曲线。

具体实施方式

以下结合附图对本发明作进一步说明，本发明包括以下步骤：

㈠：利用区间二型t-s模糊模型对网络控制进行建立模型，用if-then规则描述网络控制系统如下：

其中，nai是前件变量θa(x(t))(a＝1,2,…,p)在第i(i＝1,…,r)条规则下的模糊集；是系统状态向量；是控制输入向量；是干扰向量，且ω(t)∈l2[0,∞)；是输出向量；ai,b1i,b2i,ci,di是具有适当维数的常数矩阵；δai,δb1i是参数不确定性矩阵，且[δaiδb1i]＝hif(t)[eaiebi]；ηi,eai,ebi是已知矩阵，f(t)是未知矩阵，且满足f^t(t)f(t)≤i。

㈡：在不确定网络控制系统中加入隶属度函数，通过单点模糊化、乘积推理和中心平均去模糊化，上述系统的全局模型可写为：

其中，[hi^l(x(t))hi^u(x(t))]是第i条规则的激活强度；是θa(x(t))的上下隶属度，且式(2)中的hi(x(t))如下定义：

式(3)中αi(x(t))，是系统不确定相关的非线性函数，且满足

㈢：在控制器中加入执行器容错控制矩阵：

考虑执行器失效模型：

u^f(t)＝mau(t)(4)

执行器容错矩阵：mai和是一个标量。下面将给出不同执行器出现故障的情况：

⑴：如果那么mai＝0这将代表着ui^f(t)执行器完全失效。

⑵：当那么mai＝1这将代表着ui^f(t)执行器完全有效。

⑶：当这将代表着ui^f(t)执行器部分失效。

假设传感器是时间驱动、控制器和执行器是事件驱动，网络控制时延τk＝τk^sc+τk^c+τk^ca，这里的τk^c表示控制器的计算延迟时间，由于它的值一般都较小可做忽略处理，τk^sc表示传感器到控制器的延迟时间，τk^ca表示控制器到执行器的延迟时间。

㈣：设计网络控制系统中的状态反馈控制器，采用并行分布补偿法(pdc)，模糊控制规则如下：

其中,kj(j＝1,2,…,r)为第j个控制规则的反馈增益矩阵，h是信号的采样周期，tkh是第k次的采样时刻。定义τ(t)＝t-tkh，时滞参数设置如下：hmm＝hm-hm，hm≤τ(t)≤hm。

以下在矩阵中的*号代表对称位置上元素的转置。状态反馈控制器的全局模型是：

为了简便计算：hi(x(t))＝hi,hj(x(tkh))＝hj^k。

㈤：将全局的状态反馈控制器代入到全局的网络控制系统中，得到完整的闭环网络系统，由(2)式和(6)式所确立的闭环模糊系统如下：

给出以下本发明中用到的四个重要的引理：

引理1对于任何xi,yi(1≤i≤r),s>0是具有适当维数实数矩阵，则：

引理2给定适当维数的矩阵d,e和对称矩阵y，则y+df(t)e+e^tf^t(t)d^t<0,对所有满足f^t(t)f(t)≤i的矩阵f(t)成立，当且仅当存在常数ε>0,使得：

y+εdd^t+ε^-1e^te<0(9)

引理3任意恒定对称矩阵z∈r^n×n,z＝z^t，标量δ>0，矢量函数定义以下积分项：

引理4假设f1,f2,…,fn：r^m→r在开集d的子集中有正值，d∈r^m。那么，在集合d中fi的相互凸组合满足：

其中：

㈥：给出判据：对于给定的hm,γ,εij(i,j＝1,2,…,r),εg(g＝1,2,…,5)非负标量，使(6)表示的系统鲁棒稳定且满足h∞性能指标γ的充分条件：存在以下适当维数的矩阵y>0，xj满足ψ^ij<0。对于任意的1≤i≤j≤r，ψ^ij如下所示：

ψ¹³＝-ε3y^tai^t,ψ¹⁴＝-ε1b1imaxj-ε4y^tai^t,ψ¹⁵＝z1-ε5y^tai^t

ψ¹⁶＝-ε1b2i,ψ¹⁷＝y^tci^t,ψ¹⁸＝-ε1hi,ψ¹⁹＝y^teai^t

ψ²⁴＝-ε2b1imaxj+ε4y^t,ψ²⁵＝ε5y^t,ψ²⁶＝-ε2b2i，ψ²⁸＝-ε2hi

ψ⁸⁸＝-εij^-1i；ψ⁹⁹＝-εiji

㈦：给出以下证明：构造如下lyapunov-krasovskii泛函

v(t)＝v1(t)+v2(t)+v3(t)(12)

v1(t)＝x^t(t)px(t)

其中p，ql，zl(l＝1,2)为适当维数的正定对称矩阵，沿着系统轨线对v(t)求导得：

由newton-leibniz公式可得(16)等式：

上式中：t^t＝[t1^t,t2^t,，t3^t,t4^t,t5^t,0]，综合(12)～(16)式可得：

根据引理1得：

根据引理3得：

根据引理4得：

综合(17)～(20)式及舒尔补引理得：

式(21)中的φ^ij表示如下：

φ¹¹＝-t1(ai+δai)-(αi+δai)^tt1^t+q1+q2-z1

φ¹²＝p+t1-(ai+δai)^tt2^t,φ¹³＝-(ai+δai)^tt3^t

φ¹⁴＝-t1(b1i+δb1i)makj-(ai+δai)^tt4^t

φ¹⁵＝-(ai+δai)^tt5^t+z1,φ¹⁶＝-t1b2i,φ¹⁷＝ci^t

φ²²＝hm²z1+hmm²z2+t2^t+t2,φ²³＝t3^t

φ²⁴＝-t2(b1i+δb1i)makj+t4^t,φ²⁵＝t5^t,φ²⁶＝-t2b2i

φ³³＝-q1-z2,φ³⁴＝-t3(b1i+δb1i)makj-m12^t+z2

φ³⁵＝m12^t,φ³⁶＝-t3b2i

φ⁴⁴＝-2z2+m12+m12^t-t4(b1i+δb1i)makj-kj^tma^t(b1i+δb1i)^tt4^t

φ⁴⁵＝z2-m12^t-kj^tma^t(b1i+δb1i)^tt5^t,φ⁴⁶＝-t4b2i

φ⁴⁷＝kj^tma^tdi^t,φ⁵⁵＝-q2-z1-z2,φ⁵⁶＝-t5b2i,φ⁶⁶＝-γ²i

如果φ0^ij表示的是不含不确定矩阵δai和δb1i后的矩阵，φδ^ij则是含有不确定矩阵δai和δb1i的矩阵，那么φ^ij可有这两个矩阵表示为:

φ^ij＝φ0^ij+φδ^ij＝φ0^ij+gif(t)ei+ei^tf^t(t)gi^t(22)

式(22)中的gi、ei如下所示：

gi^t＝-hi^t[t1^t,t2^t,t3^t,t4^t,t5^t,0,0],ei＝[eai,0,0,ebikj,0,0,0]

式(22)由schur补引理及引理2可得到ξ^ij：

令对于式(23)左乘右乘这个对角矩阵的转置矩阵，且xj＝kjy。用分别代替tg，得到ψ^ij矩阵。对于ψ^ij<0成立，则由式(21)可得：

对于上式(24)左右两端同时在t∈[0,∞)上积分可得下式，且在零初始条件下v(0)＝0,v(∞)≥0。

所以：而可以进一步得出：

由式(24)～(26)可以观察出当ω(t)＝0时此时系统是渐近稳定的，且满足h∞性能指标值γ。

考虑如下非线性的弹簧-质点系统：

其归一化隶属度函数分别为：

假设状态变量x1∈[-1,1],x2∈[-1,1]，是一个外界干扰，然后选择如下的区间二型t-s模糊系统来表示上述(27)式表征的系统：

(28)式表征的系统中矩阵及用到的参数选取如下：

ε1＝1.13,ε2＝1.3285,ε3＝1.4287,ε4＝0.5746,ε5＝1,ε11＝10,ε12＝10,ε21＝5,ε22＝10

取hm＝0,γ＝0.6，可计算出时滞上界hm为0.5115。根据定理1用matlab软件中的lmi工具可求得可行解为：

初始值为x1(0)＝0.8,x2(0)＝-0.85，取τ(t)＝t-0.01k,t∈[0.01k,0.01(k+1)](k＝0,1,...)1,…)即采样周期为0.01s。针对执行器正常和各种异常情况时取ma＝diag{1,1}此时执行器正常，ma＝diag{0,1}此时执行器1完全失效，ma＝diag{1,0}此时执行器2完全失效，ma＝diag{0.5,0.5}此时执行器1，2部分失效。

由图2和图3知在执行器发生故障时，网络控制系统仍然是保持稳定的，只是在到达稳定的时间有些细微的差别。说明采用本文所述设计方法的容错控制器可使具有时延的不确定网络控制系统，在是执行器发生故障时具有鲁棒完整性。