一种基于超体积迭代全局优化算法的确定最优结构尺寸的方法与流程
本发明涉及结构尺寸优化的
技术领域:
,具体涉及一种基于超体积迭代全局优化算法的确定最优结构尺寸的方法
背景技术:
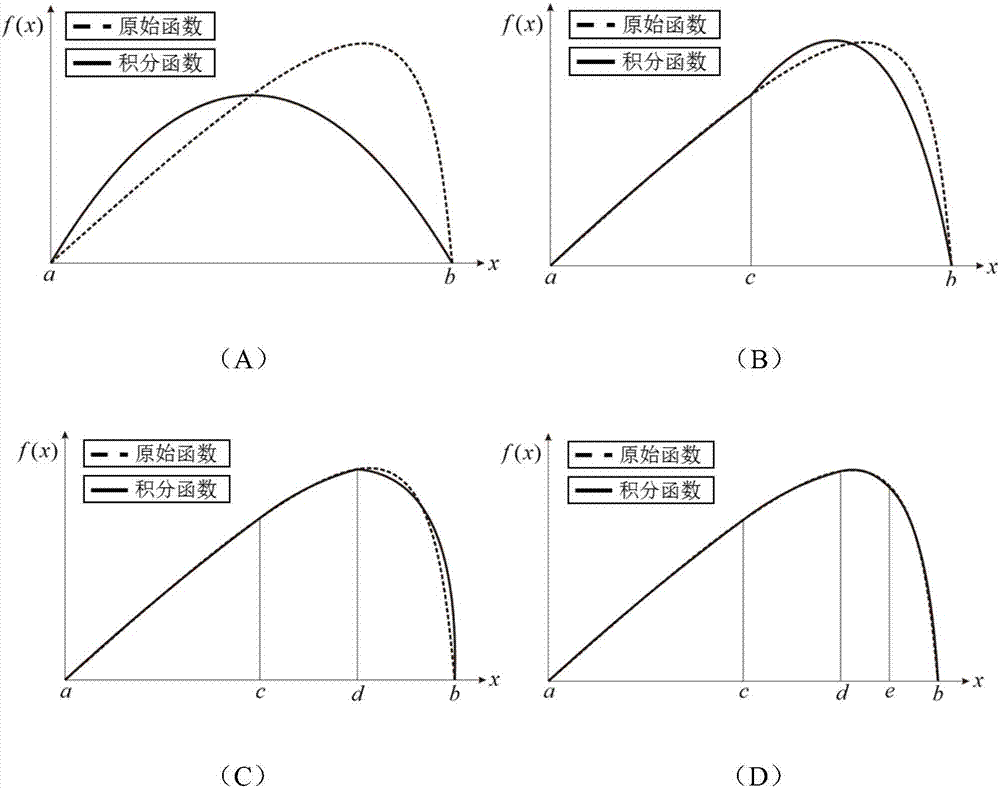
:客观世界基本上是非线性的,寻找非线性函数的最优值在工程、科学、管理学、经济学上都有很大的作用。例如在航空航天工程中需要确定最优的结构尺寸和最优的气动外形参数,从而达到减轻结构重量,提高飞行器气动效率,进而提高飞行器性能的目的;在机器学习以及模式识别领域,需要优化神经网络的各个连接节点的权值以使训练误差最小;在化学领域,需要确定试剂的最佳配比,从而达到最佳的反应效果;在生物学领域,需要预测蛋白质结构的最佳构型(proteinstructureprediction);在管理学领域,需要对生产流程进行优化,降低生产成本;在经济学领域,需要确定最优的产出,从而达到最大化利润的目的。结构尺寸优化在机械、船舶、车辆和航空航天等工程中重要的部分。采取最优的结构尺寸能够使得结构重量大大降低,从而提高装备的各项性能以及经济性。结构尺寸优化是指通过确定结构的尺寸使得结构响应目标函数最小或者最大或者与给定要求最接近。一般来说结构的响应函数都是非线性的。寻找非线性函数的全局最优值有如下的难点:(i)容易陷入局部最优:现如今很多成熟的优化算法(例如最速下降法等凸优化方法)都属于贪心类只能够找到局部最优值。(ii)梯度类的算法需要函数的导数信息,这对于非光滑函数或者隐函数不适用。(iii)当变量维度很高时,现有方法计算量很大。针对非线性结构响应的目标函数的全局最优化问题,现有方法主要分为两类:确定性全局优化方法和随机类全局优化算法。确定性的优化算法主要包括区间方法、隧道方法和trust方法等。区间方法所需要的计算量和存储空间都很大;隧道方法需要求解非线性方程的根,这也十分耗费计算时间的,而且它没有确定的收敛准则;当有多个全局最优值时,trust方法只能找到其中一个值,在多变量问题中,trust方法的搜索方向是确定的,因而其无法保证多元函数求最优值的收敛性。随机类方法主要包括模拟退火算法、粒子群算法、遗传算法等。这些算法通用性较强,适合移植于各类问题,但是这类算法容易陷入早熟,并且有时候计算效率甚至不如穷举法。由于结构尺寸优化类问题在机械、船舶、车辆和航空航天领域有着举足轻重的作用,因而建立一种计算量较小、有明确收敛准则的结构尺寸的全局优化方法有着显著的现实意义。技术实现要素:本发明要解决的技术问题是:本发明提供了一种基于超体积迭代全局优化算法的确定最优结构尺寸的方法。该方法利用超体积迭代全局优化算法确定最优的结构尺寸。该方法可用于结构响应的目标函数连续或者不连续,可导或者不可导,隐式或者显式的情况。并且该方法的计算量较小、有明确收敛准则。本发明采用的技术方案为:一种基于超体积迭代全局优化算法的确定最优结构尺寸的方法,该方法主要包括如下步骤:第一步:确定结构优化的设计变量(如杆长、梁的横截面积或者板的厚度等),确定约束条件(如位移、应力和振动频率等)。再根据有限元法、有限单元法、无网格法或者是其它的解析方法得到结构响应的目标函数。再根据实际工程情况定义设计变量的设计域和迭代的容差ε。第二步:利用辛普森自适应积分准则在设计变量的设计域内撒点,具体实现手段如下。如图2所示,结构响应的目标函数记为f(x)。首先分别取设计区间的端点和中点,记为a,b,c。取a,b,c三点,利用辛普森公式计算函数与坐标轴的包络面积,记为s1,一维情况下辛普森公式为:用中点c将设计变量的设计域分为两个子区间[a,b]和[b,c]。取[a,b]的中点记为d,取[b,c]的中点记为e,再分别取a,d,b和b,e,c,利用辛普森公式分别计算出子区间与函数的包络面积,分别记为s2和s3。利用第一步给定的容差ε,如果满足|s-(s2+s1)|≤ε,即可认为迭代已经收敛,可以停止划分子区间,反之继续划分,直到满足收敛条件。(每次计算只涉及设计变量的子区间和其相对应的母区间,而不涉及更前一代的区间,只要满足收敛条件,即对该设计变量的子区间停止划分),得到的积分节点的示意图如图3所示。高维情况是一维情况的一种扩展。在高维情况下只需要将一维定义下的面积s改为超体积i即可。其满足的收敛条件为:其中n为目标函数的维数,i为母区间的超体积,iii=1,2,...,2n为其相对应的子区间的超体积。相应的辛普森公式也应该改为高维情况,以二维情况为例,此时相应的辛普森积分公式为:其得到的积分节点示意图如图4所示。第三步:提取积分节点,并且找到当前使得结构响应目标函数最小或者最大或者与给定要求最接近的点以进行第二级优化。由于当前使得结构响应目标函数最小或者最大或者与给定要求最接近的点可以认为在响应函数全局最优值的附近,因而可以采用传统的凸优化方法对当前最优值进行优化。例如如果目标函数连续可导,则可用牛顿法或者是最速下降法等方法;如果目标函数非连续,则可用鲍威尔法或者是单纯形法等。经过两级优化之后就能够精确的找到使得结构响应函数达到要求的结构设计变量的全局最优值。其中,所述的步骤一中首先根据实际工程情况确定设计变量、设计变量的取值区间、容差和结构的约束条件等。再通过其他成熟的方法得到结构响应函数。其中,所述的步骤二中使用超体积迭代全局优化算法对结构的响应函数进行第一级优化,从而得到设计变量的近似最优解。其中,所述的步骤三中提取步骤二中产生的使得结构响应目标函数最小或者最大或者与给定要求最接近的积分节点,并利用较为成熟的凸优化方法找到结构设计变量精确的全局最优值。本发明的原理在于:一种基于超体积迭代全局优化算法的确定最优结构尺寸的方法。该方法利用超体积迭代全局优化算法对结构响应(如位移、频率以及应力等)的目标函数进行寻优,从而确定最优的结构尺寸。该方法可用于结构响应的目标函数连续或者不连续,可导或者不可导,隐式或者显式的情况。该优化首先算法利用自适应辛普森公式计算结构响应目标函数的超体积并作为迭代收敛准则,再提取积分节点并选取使得响应最小或最大或者是满足给定值的点作为近似全局最优解,最后再使用其它凸优化方法对前面找到的近似最优解进行迭代以找到全局最优值,从而最终得到结构的最优尺寸。本发明与现有技术相比的优点在于:(1)本发明对结构响应的目标函数的性质要求比较低,只要响应函数满足可积条件即可。因而可对可导或非可导、隐式或显示、连续或者不连续的目标响应函数求全局最优值;(2)本发明有一个定义良好的停止条件,而不像随机算法一样不知道在何时收敛;(3)当目标响应函数含有多个全局最优值的时候,本发明能够将它们全部找出,而传统的许多方法只能找到一个全局最优值。附图说明图1是本发明通过超体积迭代全局优化算法确定最优结构尺寸的流程图;图2是本发明在一维情况下自适应划分设计变量子区间的示意图,其中,图2(a)为不划分子区间时的原始函数和积分函数;图2(b)为将原始区间划分为两个子区间时的原始函数和积分函数;图2(c)为将图2(b)中右边的子区间继续划分为两个子区间时的原始函数和积分函数;图2(d)为最终收敛时的原始函数和积分函数;图3是本发明在一维情况下得到的积分节点以及结构响应函数全局最优值,其中,图3(a)为设计域内积分节点的分布图;图3(b)显示了积分节点与全局最优值之间的关系;图4是本发明在二维情况下得到的积分节点以及结构响应函数全局最优值,其中,图4(a)为积分节点的三维分布图;图4(b)显示了在设计域内积分节点的二维分布图;图5是实施例一中检验本发明的典型的结构响应函数的图像,其中,图5(a)为一维多峰函数和其全局最优值,图5(b)为一维多峰函数和其全局最优值,图5(c)为二维多峰函数和其全局最优值,图5(d)为二维多峰函数和其全局最优值,图5(e)为二维多峰函数和其全局最优值,图5(f)为二维多峰函数和其全局最优值;图6是实施例二中检验本发明的需要被优化的结构的示意图;图7是实施例二中经过有限元离散化之后的需要被优化的结构的示意图;图8是实施例二中迭代过程中误差随迭代步数变化的曲线图。具体实施方式下面结合附图以及具体实施例进一步说明本发明。如图1所示,本发明为一种基于超体积迭代全局优化算法的确定最优结构尺寸的方法,包括以下步骤:第一步:确定结构优化的设计变量(如杆长、梁的横截面积或者板的厚度等),确定约束条件(如位移、应力和振动频率等)。再根据有限元法、有限单元法、无网格法或者是其它的解析方法得到结构响应的目标函数。再根据实际工程情况定义设计变量的设计域和迭代的容差ε。第二步:利用辛普森自适应积分准则在设计变量的设计域内撒点,具体实现手段如下。如图2所示,结构响应的目标函数记为f(x)。首先分别取设计区间的端点和中点,记为a,b,c。取a,b,c三点,利用辛普森公式计算函数与坐标轴的包络面积,记为s1,一维情况下辛普森公式为用中点c将设计变量的设计域分为两个子区间[a,b]和[b,c]。取[a,b]的中点记为d,取[b,c]的中点记为e,再分别取a,d,b和b,e,c,利用辛普森公式分别计算出子区间与函数的包络面积,分别记为s2和s3。利用第一步给定的容差ε,如果满足|s-(s2+s1)|≤ε,即可认为迭代已经收敛,可以停止划分子区间,反之继续划分,直到满足收敛条件。(每次计算只涉及设计变量的子区间和其相对应的母区间,而不涉及更前一代的区间,只要满足收敛条件,即对该设计变量的子区间停止划分),得到的积分节点的示意图如图3所示。高维情况是一维情况的一种扩展。在高维情况下只需要将一维定义下的面积s改为超体积i即可。其满足的收敛条件为:其中n为目标函数的维数,i为母区间的超体积,iii=1,2,...,2n为其相对应的子区间的超体积。相应的辛普森公式也应该改为高维情况,以二维情况为例,此时相应的辛普森积分公式为:其得到的积分节点示意图如图4所示。第三步:提取积分节点,并且找到当前使得结构响应目标函数最小或者最大或者与给定要求最接近的点以进行第二级优化。由于当前使得结构响应目标函数最小或者最大或者与给定要求最接近的点可以认为在响应函数全局最优值的附近,因而可以采用传统的凸优化方法对当前最优值进行优化。例如如果目标函数连续可导,则可用牛顿法或者是最速下降法等方法;如果目标函数非连续,则可用鲍威尔法或者是单纯形法等。经过两级优化之后就能够精确的找到使得结构响应函数达到要求的结构设计变量的全局最优值。实施例一:为了更充分地了解该发明的特点及其解决结构尺寸全局优化问题的能力,现用本发明对如图5所示的典型的结构响应函数寻找全局最优值。与本发明相比较的方法的名称如表3所示,被比较的对象为优化过程中调用目标响应函数的次数,这也是常用的指标。目标响应函数的性质如表4所示。得到的结果如表1和表2所示。表1是本发明以及其他方法对典型结构响应函数进行全局优化调用函数的次数pijbatstrzilgatrustiahvifcn.1462120453322019---209.7fcn.238178161501258609977414表2是本发明以及其他方法对典型结构响应函数进行全局优化调用函数的次数sdeaeasmsatstrustgahvifcn.3241215------59177275883030209.7fcn.4---204810822---540771530414fcn.510822------------168126063.5fcn.6------19940------74111041表3是用来和本发明相比较的其它优化算法的名称及其缩写表4是用来对本发明进行测试的典型的结构响应函数的性质从以上算例的结果可以看出,本发明能够快速的找到结构响应函数的所有的全局最优值,并且它有一个定义良好的收敛准则。实施例二:触发机构如图6所示,a端为固支端。已知l=5cm,δ=1mm,ω0=1000hz,结构材料的弹性模量e=210gpa,体积密度为7800kg/m3;构件截面均为a×a的正方形。现需要优化触发机构的横截面边长,使得当激励幅值超过5n时,b端刚好与支撑接触、接通电路开关。首先使用有限元法对目标结构进行离散化,如图7所示。通过本发明提出的方法,得到触发机构最优的横截面边长为1.61mm。本发明的方法调用目标响应函数的次数为37次,而使用遗传算法等全局优化算法需要调用110次目标响应才能够得到全局最优值,这显示了该算法速度快的优势。算法在运行过程中,第一级优化的迭代历程曲线如图8所示,第一级优化总共调用目标响应函数30次。可以看出,曲线很快就能够收敛。以上仅是本发明的具体步骤,对本发明的保护范围不构成任何限制;其可扩展应用于其它基于满应力约束准则的桁架结构拓扑优化问题的领域,凡采用等同变换或者等效替换而形成的技术方案,均落在本发明权利保护范围之内。本发明未详细阐述部分属于本领域技术人员的公知技术。当前第1页12
相关技术
网友询问留言
已有0条留言
- 还没有人留言评论。精彩留言会获得点赞!
1