一种基于空间曲线方程的机械臂空间圆弧插值算法的制作方法

本发明涉及一种空间圆弧插值算法，特别是涉及一种基于空间曲线方程的机械臂空间圆弧插值算法，属于自动控制技术领域。

背景技术：

在轨迹插值算法中，按照轨迹效果可以分为关节插值、直线插值、圆弧插值和曲线插值，主要涉及位置规划、速度规划及加速度规划等相关规划算法，位置规划一般为线性规划、多项式规划等，速度规划采用恒速、梯形、s型，加速度选择恒定加速度或变加速。

圆弧插值算法中平面圆弧插值算法较为成熟，但是空间圆弧插值存在一定困难，当前空间圆弧插值算法一般采用几何法，基于圆弧中的特性，借助几何变换关系，推导出相应的的插值点位置公式，从而获取轨迹离散点。

目前空间圆弧插值计算借助于几何方法及向量关系建立坐标系，将空间圆弧插值转化为平面圆弧插值算法，其中，第1该类型方法涉及坐标系的建立及正、逆求解问题，数据计算量大，坐标系正逆解过程未知因素较多，第2该类型方法中每段空间圆弧均需要建立相应的坐标系，不易于算法的开发和实现。

技术实现要素：

本发明的主要目的是为了提供一种基于空间曲线方程的机械臂空间圆弧插值算法，无积分、微分等运算，降低了计算难读、基于多元一次函数组求解，降低矩阵的不可逆的影响，插值点精度高，自动化程度高。

本发明的目的可以通过采用如下技术方案达到：

一种基于空间曲线方程的机械臂空间圆弧插值算法，包括以下步骤：

步骤1：人工示教空间任意不共线三点，点p0(x1,y1,z1，α1，β1，γ1)、p1(x2,y2,z2,α2，β2，γ2)、p2(x3,y3,z3,α3，β3，γ3)，将三点的关节变量值记录下来；

步骤2：基于三点确定空间圆弧的圆心，确定空间圆的方程f；

步骤3：确定两点p0、p2之间的直线方程l1，并求解过圆心c且垂直于直线l1的垂面方程q；

步骤4：联立方程q和直线l1，求解线与面的交点w(xw,yw,zw),由圆心c和点w确定空间直线方程g；

步骤5：联立直线方程g和圆方程f，求得最中心的插值点p(xp,yp,zp)，通过解的判定，确定其中一个为符合要求的插值点坐标；

步骤6：在圆弧p0、p和圆弧p、p2等点之间重复步骤3、4、5，随后同理迭代计算其他位置插值点；

步骤7：将欧拉角α，β，γ采用线性插值点的方式对机械臂的姿态进行插值，插值点个数m(不包括点p0、p1、p2)由设定时长t和插值周期t确定，且要求m个数为奇数个。

优选的，所述步骤2中，基于三点确定空间圆弧的圆心算法为圆心坐标：

pc＝(xc,yc,zc)

空间任意不共线三点坐标值：

p0＝(x0,y0,z0)；p1＝(x1,y1,z1)；p2＝(x2,y2,z2)

圆弧圆心求解：

(x0-xc)^2+(y0-yc)^2+(z0-zc)^2＝r^2；

(x1-xc)^2+(y1-yc)^2+(z1-zc)^2＝r^2；

(x2-xc)^2+(y2-yc)^2+(z2-zc)^2＝r^2；

即：

即：

-(z1-z0)*[(y1-y0)*(z2-z1)-(y2-y1)*(z1-z0)]*xc-(z1-z0)*[(x2-x1)*(z1-z0)-(x1-x0)*(z2-z1)]*yc+[(y1-y0)*[(x2-x1)*(z1-z0)-(x1-x0)*(z2-z1)]+(y1-y0)*[(y1-y0)*(z2-z1)-(y2-y1)*(z1-z0)]]＝[(x1-x0)*z0-(z1-z0)*x0]*[(y1-y0)*(z2-z1)-(y2-y1)*(z1-z0)]-[(z1-z0)*y0-(y1-y0)*z0]**[(x2-x1)*(z1-z0)-(x1-x0)*(z2-z1)]；

即：

a*[xc,yc,zc]^t＝b

矩阵求解获取圆心坐标：

[xc,yc,zc]^t＝a^-1*b

xc、yc、zc分别为圆心的横坐标、纵坐标、竖坐标。

优选的，所述步骤2中，空间圆方程f算法为，圆弧半径求解r：

r＝sqrt((x0-xc)*(x0-xc)+(y0-yc)*(y0-yc)+(z0-zc)*(z0-zc))

基于空间圆方程的标准式确定圆弧对应圆的方程f:

(x-xc)²+(y-yc)²+(z-zc)²＝r²

r为圆弧半径。

优选的，所述步骤3中，确定两点p0、p2之间的直线方程l1算法为，基于空间直线点向式由两点p0、p2之间确定弦长对应的直线方程l1：

x0、y0、z0为点p0的横坐标、纵坐标、竖坐标。

优选的，所述步骤3中，确定垂面方程q算法为，求解过圆心pc的与直线l1垂直且相交的垂面方程q:

(x2-x0)(x-xc)+(y2-y0)(y-yc)+(z2-z0)(z-zc)＝0

x2、y2、z2为p1点的横坐标、纵坐标、竖坐标。

优选的，所述步骤4中，交点w算法为，将直线l1的方程化为参数方程：

x＝x0+(x2-x0)*t；

y＝y0+(y2-y0)*t；

z＝z0+(z2-z0)*t；

并代入以上平面方程q，解得t的值，从而确定交点为w(xb,yb,zb)。

优选的，所述步骤4中，空间直线方程g算法为，由圆心c和w确定空间直线(垂直且相交与直线l1)l2：

xb、yb、zb为点w的横坐标、纵坐标、竖坐标。

优选的，所述步骤5中，最中心的插值点p算法为，空间直线方程l2、空间圆方程f联立方程：

x＝xc+(xb-xc)*t

y＝yc+(yb-yc)*t

z＝zc+(zb-zc)*t

(x-xc)²+(y-yc)²+(z-zc)²＝r²

此处应有两解，判定合理的解，确定最中心的插值点p(xp,yp,zp)。

优选的，所述步骤6中，迭代计算其他位置插值点的算法为：选择相邻两点之间确定其他插值点，获取插值点数组p[m]；插值点数组下表索引遵循以下规律，以迭代次数n为指标，涉插值点个数为m(不包括起始点p[0]和终止点p[m+1])：

推导出：

m＝2⁰+2¹+...+2^n-1

在程序中应用case，选择程序计算相应迭代次数的插值点，迭代次数选用for循环的形式。

优选的，所述姿态选用四元数插值计算，在位置插值中确定插值点的个数(由于插值方式的特殊性，要求插入奇数个点)，基于线性插值计算插值点获取位姿插值数组，将四元数值转换成旋转矩阵，基于6自由度机器人逆运动学获取插值点的关节角度值。

本发明的有益技术效果：

1、本发明的一种基于空间曲线方程的机械臂空间圆弧插值算法，避免了示教圆心或确定三点所在平面及建立相关坐标系的问题；直接采用空间方程确定插值点。

2、本发明的一种基于空间曲线方程的机械臂空间圆弧插值算法，无积分、微分等运算，降低了计算难读、基于多元一次函数组求解，降低矩阵的不可逆的影响，插值点精度高，自动化程度高。

1、本发明的一种基于空间曲线方程的机械臂空间圆弧插值算法，可实现机械臂的空间圆弧所要求的稳定性和准确性，为机械臂的工程应用垫定基础。

附图说明

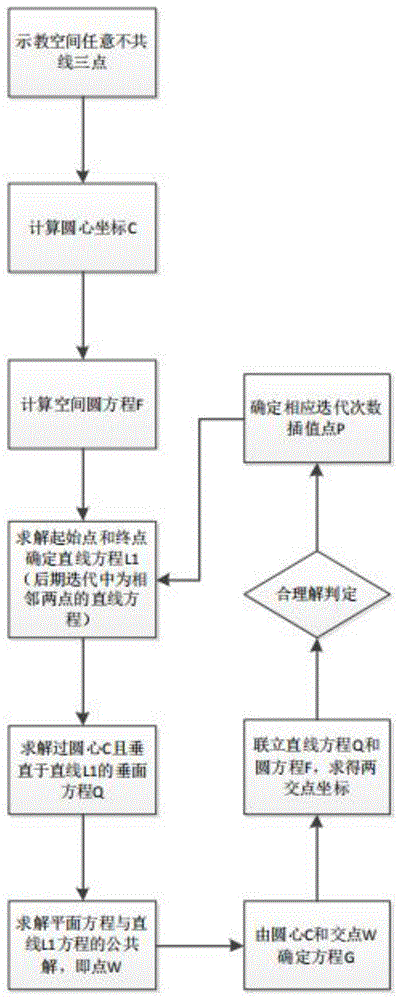
图1为按照本发明的一种基于空间曲线方程的机械臂空间圆弧插值算法的算法流程图；

图2为按照本发明的一种基于空间曲线方程的机械臂空间圆弧插值算法的一优选实施例的空间圆弧示意图；

图3为按照本发明的一种基于空间曲线方程的机械臂空间圆弧插值算法的一优选实施例的插值点p的位置索引图；

图4为按照本发明的一种基于空间曲线方程的机械臂空间圆弧插值算法的一优选实施例的插值方式示意图。

具体实施方式

为使本领域技术人员更加清楚和明确本发明的技术方案，下面结合实施例及附图对本发明作进一步详细的描述，但本发明的实施方式不限于此。

如图1-图4所示本实施例提供的一种基于空间曲线方程的机械臂空间圆弧插值算法，包括以下步骤：

步骤1：人工示教空间任意不共线三点，点p0(x1,y1,z1，α1，β1，γ1)、p1(x2,y2,z2,α2，β2，γ2)、p2(x3,y3,z3,α3，β3，γ3)，将三点的关节变量值记录下来；

步骤2：基于三点确定空间圆弧的圆心，确定空间圆的方程f；

步骤3：确定两点p0、p2之间的直线方程l1，并求解过圆心c且垂直于直线l1的垂面方程q；

步骤4：联立方程q和直线l1，求解线与面的交点w(xw,yw,zw),由圆心c和点w确定空间直线方程g；

步骤5：联立直线方程g和圆方程f，求得最中心的插值点p(xp,yp,zp)，通过解的判定，确定其中一个为符合要求的插值点坐标；

步骤6：在圆弧p0、p和圆弧p、p2等点之间重复步骤3、4、5，随后同理迭代计算其他位置插值点；

步骤7：将欧拉角α，β，γ采用线性插值点的方式对机械臂的姿态进行插值，插值点个数m(不包括点p0、p1、p2)由设定时长t和插值周期t确定，且要求m个数为奇数个。

在实施例中，如图2所示，步骤2中，基于三点确定空间圆弧的圆心算法为圆心坐标：

pc＝(xc,yc,zc)

空间任意不共线三点坐标值：

p0＝(x0,y0,z0)；p1＝(x1,y1,z1)；p2＝(x2,y2,z2)

圆弧圆心求解：

(x0-xc)^2+(y0-yc)^2+(z0-zc)^2＝r^2；

(x1-xc)^2+(y1-yc)^2+(z1-zc)^2＝r^2；

(x2-xc)^2+(y2-yc)^2+(z2-zc)^2＝r^2；

即：

即：

-(z1-z0)*[(y1-y0)*(z2-z1)-(y2-y1)*(z1-z0)]*xc-(z1-z0)*[(x2-x1)*(z1-z0)-(x1-x0)*(z2-z1)]*yc+[(y1-y0)*[(x2-x1)*(z1-z0)-(x1-x0)*(z2-z1)]+(y1-y0)*[(y1-y0)*(z2-z1)-(y2-y1)*(z1-z0)]]＝[(x1-x0)*z0-(z1-z0)*x0]*[(y1-y0)*(z2-z1)-(y2-y1)*(z1-z0)]-[(z1-z0)*y0-(y1-y0)*z0]**[(x2-x1)*(z1-z0)-(x1-x0)*(z2-z1)]；

即：

a*[xc,yc,zc]^t＝b

矩阵求解获取圆心坐标：

[xc,yc,zc]^t＝a^-1*b

xc、yc、zc分别为圆心的横坐标、纵坐标、竖坐标。

在实施例中，所示步骤2中，空间圆方程f算法为，圆弧半径求解r：

r＝sqrt((x0-xc)*(x0-xc)+(y0-yc)*(y0-yc)+(z0-zc)*(z0-zc))

基于空间圆方程的标准式确定圆弧对应圆的方程f:

(x-xc)²+(y-yc)²+(z-zc)²＝r²

r为圆弧半径。

在实施例中，所示步骤3中，确定两点p0、p2之间的直线方程l1算法为，基于空间直线点向式由两点p0、p2之间确定弦长对应的直线方程l1：

x0、y0、z0为点p0的横坐标、纵坐标、竖坐标。

在实施例中，所示步骤3中，确定垂面方程q算法为，求解过圆心pc的与直线l1垂直且相交的垂面方程q:

(x2-x0)(x-xc)+(y2-y0)(y-yc)+(z2-z0)(z-zc)＝0

x2、y2、z2为p1点的横坐标、纵坐标、竖坐标。

在实施例中，所示步骤4中，交点w算法为，将直线l1的方程(3)化为参数方程：

x＝x0+(x2-x0)*t；

y＝y0+(y2-y0)*t；

z＝z0+(z2-z0)*t；

并代入以上平面方程q，解得t的值，从而确定交点为w(xb,yb,zb)。

在实施例中，所示步骤4中，空间直线方程g算法为，由圆心c和w确定空间直线(垂直且相交与直线l1)l2：

xb、yb、zb为点w的横坐标、纵坐标、竖坐标。

在实施例中，所示步骤5中，最中心的插值点p算法为，空间直线方程l2、空间圆方程f联立方程：

x＝xc+(xb-xc)*t

y＝yc+(yb-yc)*t

z＝zc+(zb-zc)*t

(x-xc)²+(y-yc)²+(z-zc)²＝r²

此处应有两解，判定合理的解，确定最中心的插值点p(xp,yp,zp)。

在实施例中，如图4所示步骤6中，迭代计算其他位置插值点的算法为：选择相邻两点之间确定其他插值点，获取插值点数组p[m]；插值点数组下表索引遵循以下规律，以迭代次数n为指标，涉插值点个数为m(不包括起始点p[0]和终止点p[m+1])：

推导出：

m＝2⁰+2¹+...+2^n-1

在程序中应用case，选择程序计算相应迭代次数的插值点，迭代次数选用for循环的形式，确保每个迭代次数的值均被计算，且被放入数组指定位置。

在实施例中，如图4所示姿态选用四元数插值计算，在位置插值中确定插值点的个数(由于插值方式的特殊性，要求插入奇数个点)，基于线性插值计算插值点获取位姿插值数组，将四元数值转换成旋转矩阵，基于6自由度机器人逆运动学获取插值点的关节角度值。

综上所述，在本实施例中，避免了示教圆心或确定三点所在平面及建立相关坐标系的问题；直接采用空间方程确定插值点，无积分、微分等运算，降低了计算难读、基于多元一次函数组求解，降低矩阵的不可逆的影响，插值点精度高，自动化程度高，可实现机械臂的空间圆弧所要求的稳定性和准确性，为机械臂的工程应用垫定基础。

以上所述，仅为本发明进一步的实施例，但本发明的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明所公开的范围内，根据本发明的技术方案及其构思加以等同替换或改变，都属于本发明的保护范围。