一种高空作业平台臂架变幅振动特性的研究方法与流程

本发明涉及一种高空作业平台臂架变幅振动特性的研究方法，属于高空作业平台臂架振动控制技术领域。

背景技术：

高空作业平台是一种将人员和设备举升到一定高度进行操作的装备。随着工程实际中工作高度的增加，高空作业车的臂架长度越来越大，甚至超过百米以上，因而对人在臂架上的安全性和舒适型的要求就会进一步提高，为了保证此要求，必须要严格控制和减小臂架的振动。而目前针对变幅运动的振动研究中，在建立臂架模型时，均将臂架的变幅系统简化为具有转动惯量的驱动轮毂，忽略臂架根铰点与变幅油缸铰点之间的距离，即将臂架尾部和变幅油缸组成的三角区域视为刚性区域，故臂架变成了变截面的悬臂梁结构。这种简化忽略了高空作业平台的实际情况，可能会为臂架振动的抑制与控制带来误差。

技术实现要素：

本发明要解决的技术问题是，克服现有技术的缺陷，提供一种能够解决现有高空作业平台变幅运动过程中，随着随着变幅仰角变化，臂架头部的振动响应计算不准确不符合工程实际等问题的高空作业平台臂架变幅振动特性的研究方法。

为解决上述技术问题，本发明采用的技术方案为：

一种高空作业平台臂架变幅振动特性的研究方法，包括以下步骤：

s01，对变幅液压油缸进行弹簧的等效，将活塞杆两侧的液压油等效为并联的液压油弹簧，将活塞杆本身等效为与液压油弹簧串联，得到等效后刚度计算模型；

s02，利用哈密顿原理计算得出边界条件、连续性条件以及动力学微分方程；

s03，对s02得出的非齐次振动微分方程进行齐次化，结合欧拉伯努利梁振动特性，利用拉普拉斯变换与反拉普拉斯变换得出振型初步解；

s04，利用边界条件、连续性条件、齐次微分方程结合振型初步解得出振动的齐次微分方程组，得出振动特征值；

s05，结合模态振型之间的正交性得到希尔伯特空间内的振动的状态空间方程；

s06，在matlab/simulink环境下进行动态仿真，得到随着仰角变化，臂架头部的振动响应。

s01中，变幅液压油缸弹性支承的变幅缸等效刚度k取值于液压油弹簧刚度，其计算方式如下：

其中，x代表液压缸活塞位移距离，l代表行程，ak、ar分别代表液压缸左右两侧工作面积，vk、vr分别代表液压缸左右两侧容积，vlk、vlr分别代表液压缸两侧管道内油液死容积，βe为液压油体积模量。

s02中，将整个臂架划分n段具有集中参数又相互连续的臂节，利用哈密顿原理公式：其中，t1、t2分别为运动开始时间与结束时间，t为臂架动能，w为非保守力虚功，v为臂架势能；

式中：分别代表臂节i与i-1连接处右偏差与左偏差，z代表臂架上点沿z轴与原点的距离，ρai代表臂节i的线密度,代表变幅运动角度θ(t)对时间t求导，代表臂节中性轴挠度ω(z,t)对时间t求导，mc、jc分别代表臂架顶部的集中质量和转动惯量，l代表臂架总长度，代表代表臂架顶部挠度ω(l,t)对时间t的导数，代表臂架顶部挠度ω(l,t)对时间t与坐标z的导数；

考虑臂架势能v时，将得到的等效弹簧势能考虑进去，

w＝mθ(t)

式中：eii代表臂节i的抗弯密度，ω″(z,t)代表臂架的中性轴挠度ω(z,t)对坐标z求二次导，g代表惯性加速度，k代表变幅缸等效刚度，l0代表臂架初始状态下变幅缸长度，l1代表当前变幅缸长度，a代表变幅缸铰接点到臂架底部距离，ω(a,t)代表液压缸铰接点处臂架的中性轴挠度，α代表变幅缸与臂架的夹角，m表示变幅油缸对臂架的驱动力矩。

动力学微分方程、边界条件、连续条件分别如下式：

式中：v(z,t)表示臂架上某点到水平线的弧度，下标i表示第i节臂，且有：vi(z,t)＝zθ+ω(z,t),z∈(zi-1⁺,zi^-)，vi^ⅳ(z,t)代表对位移坐标z的四次导数，代表对时间t的二次导数，kα表示变幅缸等效刚度k与(sinα)²的乘积，δ1(z-a)函数分别表示狄克雷函数，反映了仅z＝a变幅缸处支承力，h(z-z1⁺)表示单位阶跃函数，代表臂架末端弧度对时间t的二次导数以及对位移坐标z的一次导数，vn″(l,t)、vn″(l,t)分别代表臂架末端弧度对位移坐标z的二和三次导数，代表臂架末端弧度对时间t的二次导数，和分别连续臂节i和i+1处弧度对位移坐标z的二次和三次导数。

s03中，欧拉伯努利梁振动特性为w²＝eiiγi⁴/ρai，其中w为梁振动固有频率，γi为频率特征值，

且动力学响应vi(z,t)可由广义振型基函数和广义坐标q(t)表示：

其中下标b表示第b阶振型，代表任意臂节i的b阶振型基函数将其代入动力学微分方程可得：

其中为振型基函数对位移坐标z的四次导数。

对其进行拉普拉斯变换与反拉普拉斯变换得出振型的初步解；

其中：cosh与sinh分别为双曲余弦与双曲正弦函数，

s04中，齐次方程组为mnpn＝0，其中

式中：mn表示齐次方程的系数矩阵、b1和bn分别代表臂架底部与顶端的边界条件系数、ci(z)代表臂架的连续条件的系数矩阵、pn是由振型函数及其导数组成的系数向量；

且有：e＝γn(l-zn-1)、x1＝γi(z-zi-1⁺)、x3＝γi(z-a)、h2＝ct(γia)h(zi-a)[1-h(zi-z1)]、h3＝cv(γia)h(zi-a)[1-h(zi-z1)]。

利用s04中的臂架振动微分方程的通解v(z,t)，根据其正交性，取臂架末端前三阶振型解v1(t)、v2(t)、v3(t)可获得s05中的前三阶主坐标振动微分方程，

式中：和表示前三阶振型解的二阶导，和表示前三阶振型解的一阶导，ξ1、ξ2和ξ3为前三阶振型的阻尼比，w1、w2和w3分为前三阶固有频率，f为非齐次项模态动载荷，为建立希尔伯特空间内的振动的状态空间方程，定义状态向量为：

则有

其中：g＝[g1(t)g2(t)g3(t)g4(t)g5(t)g6(t)]^t，u＝θ，b＝[0w1²f0w2²f0w3²f]^t，d＝0

式中：和分为前三阶臂架末端的振型基函数。

本发明的有益效果：本发明提供的一种高空作业平台臂架变幅振动特性的研究方法，主要针对变幅机构中的变幅液压缸进行弹簧等效，将其变幅液压缸视为弹性支承，避免将变幅油缸、臂架和转台所组成的三角部分直接简化为刚性区域，这样能更好地反映出臂架头部(即工作平台)在变幅运动中的振型与频率；同时，本文将计入变幅液压缸的等效弹簧刚度计算所得出的振型与固有频率代入臂架振动的状态空间方程，在matlab/simulink环境下进行动态仿真，得出臂架头部的振动响应。本发明提供的一种高空作业平台臂架变幅振动特性的研究方法，能够提高臂架头部振幅计算的准确性，为高空作业平台的振动控制提供了更为精确的理论参考。

附图说明

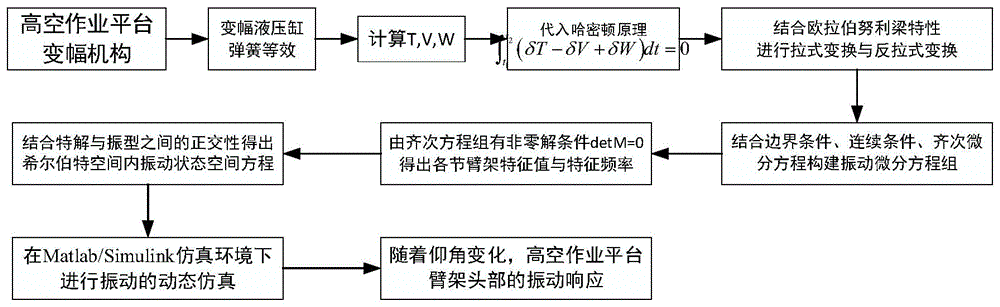
图1是本发明一种高空作业平台臂架变幅振动特性的研究方法的过程示意图；

图2是本发明中高空作业平台模型等效示意图；

图3是本发明中变幅液压缸液压弹簧等效示意图；

图4是本发明中臂架振型曲线；

图5是本发明中臂架头部振动速度响应曲线；

图6是本发明中臂架位移弧长响应；

图7是本发明中考虑变幅液压缸弹性刚度与刚性区域的振动响应对比。

具体实施方式

下面结合附图对本发明作进一步描述，以下实施例仅用于更加清楚地说明本发明的技术方案，而不能以此来限制本发明的保护范围。

下面以某型号全长为35.35米的高空作业平台为研究对象(具体参数如表1)，对本发明所提出的研究方法进行说明：

表1臂架具体参数

如图1所示，本发明公开一种高空作业平台臂架变幅振动特性的研究方法，包括以下步骤：

步骤一，对变幅液压油缸进行弹簧的等效，将活塞杆两侧的液压油等效为并联的液压油弹簧，将活塞杆本身等效为与液压油弹簧串联，得到等效后刚度计算模型，具体如图3所示。

由于活塞杆刚度远大于液压油刚度，故计算变幅油缸弹性支支承的等效刚度时可忽略活塞杆的刚度，变幅液压油缸弹性支承的变幅缸等效刚度k取值于液压油弹簧刚度，其计算方式如下：

其中，x代表液压缸活塞位移距离，l代表行程，ak、ar分别代表液压缸左右两侧工作面积，vk、vr分别代表液压缸左右两侧容积，vlk、vlr分别代表液压缸两侧管道内油液死容积，βe为液压油体积模量。

步骤二，利用哈密顿原理计算得出边界条件、连续性条件以及动力学微分方程。哈密顿原理公式为：其中，t1、t2分别为运动开始时间与结束时间，t为臂架动能，w为非保守力虚功，v为臂架势能，高空作业平台模型等效示意图如图2所示。

式中：代表对时间t求导，代表臂架的中性轴挠度对时间t求导，代表代表臂架顶部挠度对时间t的导数、分别代表臂节i与i-1连接处右偏差与左偏差，代表臂架顶部挠度对时间t与坐标z的导数；

考虑臂架势能v时，将得到的等效弹簧势能考虑进去，

w＝mθ(t)

式中：m表示变幅油缸对臂架的驱动力矩，ρai、eii、vi分别代表臂节i的线密度、抗弯密度和速度，zi代表臂节i沿z轴与原点的距离，ω(z,t)代表臂架的中性轴挠度，上标ω′代表对坐标z求导，g代表惯性加速度，θ代表臂架的变幅角度，k代表变幅缸等效刚度，l0代表臂架初始状态下变幅缸长度，l1代表当前变幅缸长度，l代表臂架总长度，a代表变幅缸铰接点到臂架底部距离，ω(a,t)代表液压缸铰接点处臂架的中性轴挠度，α代表变幅缸与臂架的夹角，mc、jc分别代表臂架顶部的集中质量和转动惯量，ω(l,t)代表臂架末端的中性轴挠度，ω”(z,t)代表臂架的中性轴挠度对坐标z二次导数。

通过上式可得动力学微分方程、边界条件、连续条件分别如下式；

式中：kα表示变幅缸等效刚度k与(sinα)²的乘积，h(z-z1⁺)表示单位阶跃函数，δ1(z-a)函数分别表示狄克雷函数，狄克雷函数反映了仅z＝a变幅缸处支承力，vi(z,t)表示臂架上某点到水平线的弧度，且有：vi(z,t)＝zθ+ω(z,t),z∈(zi-1⁺,zi^-)；

其中，vi^ⅳ(z,t)、分别代表vi(z,t)对位移坐标z的四次、三次与两次求导；代表vi(z,t)对时间t的二次导数；代表臂架末端vi(z,t)对时间t的二次导数以及对位移坐标z的一次导数。

步骤三，对步骤二得出的非齐次振动微分方程进行齐次化，结合欧拉伯努利梁振动特性，利用拉普拉斯变换与反拉普拉斯变换得出振型初步解。

欧拉伯努利梁振动特性为ω²＝eiiγi⁴/ρai，其中w为梁振动固有频率，γi为频率特征值，

且动力学响应vi(z,t)可由振型函数和广义坐标q(t)表示为：

其中下标b表示第b阶振型，代表任意臂节i的b阶振型函数，将其代入动力学微分方程可得：

对其进行拉普拉斯变换与反拉普拉斯变换得出振型的初步解；

其中：cosh与sinh分别为双曲余弦与双曲正弦函数，

步骤四，利用边界条件、连续性条件、齐次微分方程结合振型初步解得出振动的齐次微分方程组mnpn＝0，根据其次方程组有非零解的条件detmn＝0得出振动特征值，继而得出各节臂架的振型与振动频率；

式中：e＝γn(l-zn-1)、x1＝γi(z-zi-1⁺)、x3＝γi(z-a)、pn是由振型函数及其导数组成的系数向量，h2＝ct(γia)h(zi-a)[1-h(zi-z1)]，h3＝cv(γia)h(zi-a)[1-h(zi-z1)]。

步骤五，结合模态振型之间的正交性，考虑前三阶主坐标空间内的振动微分方程为：

式中：前三阶振型的阻尼比取为ξ1＝0.05、ξ2＝0.005、ξ3＝0.005，w分为前三阶固有频率，f为非齐次项模态动载荷，并定义状态向量为：

得到希尔伯特空间内的振动的状态空间方程其中：g＝[g1(t)g2(t)g3(t)g4(t)g5(t)g6(t)]^t，u＝θ，b＝[0w,1²f10w,2²f20w,3²f3]^t，d＝0

式中：分为前三阶臂架末端的振型函数。

步骤六，在matlab/simulink环境下进行动态仿真，得到随着仰角变化，臂架头部的振动响应。其中设定臂架的运动为：0到10s停在水平位置，10s到30.4s臂架以2°/s的速度旋转，到达50.8°后停留20s,然后以1.53°/s的速度运动到72°停止，高空作业平台臂架头部的振型图如下图4所示，速度响应如图5所示，响应位移如图6所示，对比图如图7所示。

以上所述仅是本发明的优选实施方式，应当指出：对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也应视为本发明的保护范围。