材料变形破裂的力学各向异性晶格弹簧模型仿真方法

本发明涉及数值仿真，尤其涉及一种材料变形破裂的力学各向异性晶格弹簧模型(m-alsm，mechanical anisotropic lattice spring model)仿真方法；

背景技术：

1、基于传统连续介质力学的方法如有限元法(fem)、有限差分法(fdm)、有限体积法(fvm)等已在描述固体材料变形、流体流动、介质传热及多物理场耦合问题等方面获得了巨大的成功，但在描述固体材料破裂问题方面仍面临着困难。作为基于传统连续介质力学的方法的有效替代，晶格模型(lm,lattice model)已被用于描述固体材料的变形破裂、介质传热和渗流等问题。

2、晶格模型的起源可以追溯到hrennikoff(hrennikoff,1941)开发的模拟二维弹性连续体的网格模型。晶格模型的创立初衷是通过节点连接的格构单元模拟等效连续体，如图1(a)所示。随着应用需求的不断拓展，这一思想逐渐演化为采用弹簧键连接晶格颗粒，形成类似于颗粒离散元中粘结颗粒模型(bpm)(potyondy and cundall,2004)的颗粒弹簧系统，以模拟等效连续体，如图1(b)所示。这一思想分支诞生了现今在岩石破裂模拟领域应用最为广泛的晶格模型——晶格弹簧模型(lsm,lattice spring model)，也有学者称之为弹簧网络模型(snm,spring network model)(rasmussen et al.,2018；rasmussen,2021a,2022a；rasmussen and de assis,2018)。

3、晶格弹簧模型融合了颗粒离散元中粘结颗粒模型的主要特性，能够在一个统一的框架下自然地模拟材料的变形、断裂和破碎行为，近年来在岩石破裂行为的数值研究中获得了长足发展(fu et al.,2022；li and zhao,2021；nikolic et al.,2018；omori etal.,2011；ostoja-starzewski,2002；rasmussen,2021a,2022a；rasmussen and de assis,2018；zhao,2017；zhao et al.,2019；zhou et al.,2021)，在层状岩石破裂模拟领域也得到了应用。尽管现有晶格弹簧模型在模拟层状岩石破裂问题方面展现出了巨大的潜力，但仍然存在一些缺陷，主要体现在以下几个方面：(1)非耦合刚度矩阵表达层状岩石复杂各向异性变形不准确；(2)确保弹簧刚度与介质宏观弹性常数匹配的关系式推导不严格；(3)描述不同材料泊松比多样性的可用泊松比分布存在局限性；(4)表示层状岩石层理和基体破坏的强度准则不统一。

4、(1)非耦合刚度矩阵表达层状岩石复杂各向异性变形不准确

5、层状岩石中的复杂各向异性变形需要由式(a)中的刚度矩阵来表达(enayatpouret al.,2018b；尹et al.,2005)。

6、

7、在现有的晶格弹簧模型中，为粒子传递相互作用力的弹簧主要包含三种类型(nikolic et al.,2018；omori et al.,2011)，分别为法向弹簧、切向弹簧和旋转弹簧，如图2所示。

8、最简单的模型仅包含法向弹簧，最常用的至少包含三种类型弹簧中的两种。然而，在晶格模型中使用旋转弹簧存在争议，cusatis等人(cusatis et al.,2003)指出，梁的弯曲不是微观结构中的物理现象的特征。如果不考虑旋转弹簧，则晶格弹簧模型中的弹簧刚度矩阵可以表示为式(b)中的对角矩阵，弹簧刚度之间都是非耦合的。弹簧刚度耦合效应的缺失导致晶格弹簧模型不能准确表达层状岩石中的复杂各向异性变形。大多数现有晶格弹簧模型都假面向各向同性问题开发，这也在一定程度上限制了它们在准确表达层状岩石复杂各向异性变形的能力。

9、

10、此外，颗粒尺度上的弹性响应异质性是现有晶格弹簧模型无法准确描述层状岩石中复杂各向异性变形的一个重要原因。当晶格模型中的颗粒尺寸大于实际岩石晶粒或内部长度尺度时，会导致接触应变和应力分散的过度预测，即使在均匀的宏观应变(或应力)状态下，接触应变和应力的异质性也可能显著。这种行为将导致在各向异性(甚至全压缩)应力状态下对材料强度的显著低估，以及通常过度和弥散的裂纹(damjanac et al.,2016)。

11、(2)确保弹簧刚度与介质宏观弹性常数匹配的关系式推导不严格

12、晶格弹簧模型的一个显著特征是其能够直接将弹簧刚度与介质的宏观弹性常数(如弹性模量、泊松比等)进行匹配，从而避免了类似颗粒离散元模型中确定弹簧刚度参数所需的复杂标定过程。在晶格弹簧模型中，将弹簧刚度与介质的宏观弹性常数进行匹配的方法主要有两种：第一种方法是利用介质的宏观弹性常数，结合弹簧长度和横截面积进行近似估计(ibrahimbegovic and delaplace,2003；nikolic et al.,2015；nikolic andibrahimbegovic,2015；vassaux et al.,2016,2015)，如图3(a)所示；第二种方法是基于介质弹性应变能等效的关系推导(chen et al.,2016；griffiths and mustoe,2001；liu andliu,2006；zhao et al.,2011)，如图3(b)所示。在一些特定情况下(如规则晶格弹簧模型)，这两种方法将会统一到一起(nikolic et al.,2018)。然而，第一种方法缺乏理论推导，第二种方法虽然经过了一定的理论推导，但推导过程并不严格，因为剪应力互等条件未被纳入到推导过程中。

13、(3)描述不同材料泊松比多样性的可用泊松比分布存在局限性

14、晶格弹簧模型的可用泊松比分布通常存在一定限制，如仅使用法向弹簧的晶格弹簧模型，在粒子数量趋于无穷时的泊松比趋近于一个固定值，即三维情况下为0.25，二维情况下为1/3。这种限制一般通过引入切向弹簧提供额外相互作用力来克服，也有学者通过引入旋转弹簧甚至用梁代替传统弹簧解决上述问题(nikolic et al.,2018；omori et al.,2011)。然而，cusatis等人(cusatis et al.,2003)指出，梁的弯曲不是微观结构中的物理现象的特征，研究者们试图在不引入旋转自由度的情况下克服晶格弹簧模型泊松比的限制。如zhao等人(zhao,2010,2017；zhao et al.,2011)通过分别引入切向弹簧和四维弹簧提供额外相互作用克服固定泊松比的限制，开发了离散晶格弹簧模型(dlsm)和四维离散晶格弹簧模型(4d-dlsm)。尽管如此，晶格弹簧模型的可用泊松比范围依然有限。为了进一步扩大可用泊松比分布的范围，mariotti(mariotti,2007)通过局部粒子应变估计弹簧变形，zhao等人(zhao,2010；zhao et al.,2011)也采用了类似的方法，两者区别在于采用了不同的局部粒子应变计算方式。asahina等人(asahina et al.,2017a,2015)提出了基于辅助应力的二维和三维各向同性晶格弹簧模型，从新的角度消除了传统晶格模型的泊松比限制，rasmussen和de assis(rasmussen and de assis,2018)进一步将该方法扩展到了模拟横观各向同性的晶格弹簧模型中。

15、尽管研究者们为克服晶格弹簧模型的可用泊松比分布的局限性做出了大量努力，但将现有方法用于表达层状岩石中的复杂各向异性变形依然存在一些问题。如mariotti(mariotti,2007)和zhao等人(zhao,2010；zhao et al.,2011)的方法均面向各向同性问题开发，是否适用于各向异性问题仍有待验证。此外，zhao等人(zhao,2010；zhao et al.,2011)的方法通过最小二乘法估计粒子的局部应变，难以避免方程组无解的情况。asahina等人提出的辅助应力方法以被rasmussen和deassis(rasmussen and de assis,2018)证明能够用于模拟横观各向同性问题，但他们引入的辅助应力是虚拟的，并不满足传统力学的物理内涵。

16、泊松比分布的局限性限制了晶格弹簧模型在一些层状岩石，特别是具有宽泊松比分布的层状岩石中的应用。

17、(4)表示层状岩石层理和基体破坏的强度准则不统一

18、试验研究表明，层状岩石存在两种剪切失效模式：结构面或层理面上的滑动失效和与非滑动失效相关的岩石基体破裂(tien et al.,2006)。然而，当施加的应力达到临界围压的水平，与非平面结构面或层理面剪切相关的膨胀可以被完全抑制(barton,1976)，即当岩石所受压力接近临界围压时，岩石节理的强度应等于完整岩石的强度(asadi andbagheripour,2015)。当层状岩石层理性质无限趋近于基体性质时，层理和基体应当满足相同的破坏条件，此时表示层理和基体破坏的强度准则应当自然地统一到一起。

19、tien和kuo(tien and kuo,2001)基于弹性理论的概念，提出了各向异性层状岩石的破坏准则，明确地区分了层理和基体的两种破坏模式。他们采用jaeger准则(jaeger,1960)描述的莫尔-库仑强度包络来检查岩石结构面或层理面上的的滑动失效，并使用hoek-brown强度包络(hoek and brown,1981)来检查与非滑动失效相关的岩石基体破裂。rasmussen和deassis(rasmussen and de assis,2018)将该准则应用到其发展的用于模拟横观各向同性问题的晶格弹簧模型中，并采用了双线性莫尔-库仑准则来检查岩石结构面或层理面上的的滑动失效，以更好地捕捉泥质岩层理面的抗剪切强度。rasmussen和deassis(rasmussen and de assis,2018)的晶格弹簧模型中采用的表示层状岩石层理和基体破坏的强度准则显然不统一，因为一个是线性的，一个是非线性的。此外，其他用于模拟层状岩石破裂的晶格弹簧模型(yao et al.,2016；you et al.,2011；zhao,2014b；李,2019)也存在类似的问题，且更为明显。

20、表示层状岩石层理和基体破坏的强度准则不统一为晶格弹簧模型的广泛应用带来了一定不便。

技术实现思路

1、本发明的目的在于提供一种材料变形破裂的力学各向异性晶格弹簧模型(m-alsm，mechanical anisotropic lattice spring model)仿真方法，旨在解决现有晶格弹簧模型在模拟层状岩石破裂问题方面存在困难的问题。

2、为实现上述目的，本发明提供了一种材料变形破裂的力学各向异性晶格弹簧模型(m-alsm，mechanical anisotropic lattice spring model)仿真方法，包括以下步骤：

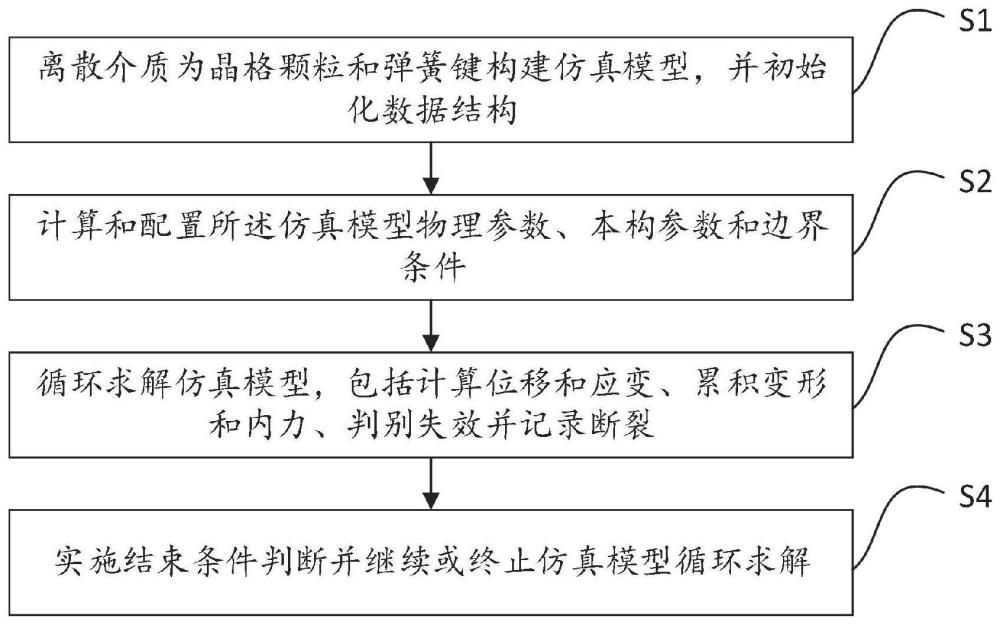
3、离散介质为晶格颗粒和弹簧键构建仿真模型，并初始化数据结构；

4、计算和配置所述仿真模型物理参数、本构参数和边界条件；

5、循环求解仿真模型，包括计算位移和应变、累积变形和内力、判别失效并记录断裂；

6、实施结束条件判断并继续或终止仿真模型循环求解。

7、其中，所述构建仿真模型包括使用delaunay三角剖分构建弹簧键网并使用对偶的voronoi图构建晶格颗粒集；

8、所述初始化数据结构包括初始化弹簧键与其两端晶格颗粒的链表数据结构和初始化晶格颗粒与其周围弹簧键的链表数据结构；

9、所述晶格颗粒具有不同的尺寸、形状和质量，并由零质量的弹簧键连接发生相互作用；

10、所述弹簧键由三根弹簧组成，三根弹簧分别为法向弹簧、切向弹簧和法向-切向耦合弹簧，每根弹簧都有其独立的刚度，所述弹簧键具有强度，当其受力超过设定强度时发生断裂。

11、其中，所述物理参数包括晶格颗粒的密度和阻尼，所述本构参数包括弹簧键的刚度参数和强度参数，所述边界条件包括晶格颗粒的体力和速度、弹簧键的预变形和预内力；

12、所述弹簧键的刚度参数由弹簧键的弹簧刚度与介质的宏观弹性常数之间的关系转换并叠加计算，如式(1)和式(2)所示；

13、k＝(ql)-1(vc)  (1)

14、

15、力学各向异性晶格弹簧模型中弹簧键的刚度参数由弹簧键的弹簧刚度与介质的宏观弹性常数之间的关系转换并叠加计算，三个弹簧键b1、b2和b3，b1法向刚度切向刚度耦合刚度单位法向量长度b2法向刚度切向刚度耦合刚度单位法向量长度b3法向刚度切向刚度耦合刚度单位法向量长度

16、k为弹簧键的弹簧刚度组成向量，表达为

17、

18、q为弹簧键的单位法向量贡献矩阵，表达为

19、

20、式中，

21、

22、

23、

24、

25、

26、

27、

28、

29、

30、

31、

32、

33、

34、

35、

36、

37、

38、

39、且b代表b1、b2和b3；

40、l为弹簧键的长度贡献矩阵，表达为

41、

42、v为等效三角形控制体积，计算为

43、

44、式中，p为三个弹簧键长度之和的平均值，计算为d为模型厚度；

45、c为介质的宏观弹性常数组成向量，表达为

46、c＝[c11 c22 4c66 c12 2c16 2c26 0 0 0]t  (7)

47、式中，c11、c22、c66、c12、c16和c26为各向异性介质的宏观弹性常数；

48、当弹簧键网格拓扑为规则形状(正三角形)时，有式(1)退化为

49、

50、进一步，当各向异性介质退化为各向同性介质时，式(8)退化为

51、

52、

53、式中，e和v分别为各向同性介质的宏观弹性模量和泊松比；

54、此外，力学各向异性晶格弹簧模型实际应用中，模型内部弹簧键的刚度由弹簧键为公共边的两个相邻三角形单元贡献的刚度叠加计算，模型边界弹簧键的刚度由弹簧键为边界的一个三角形单元贡献的刚度表征，其中，弹簧键的刚度可以具化为

55、

56、所述弹簧键的弹簧刚度与介质的宏观弹性常数之间的关系式由基于应变能相等和基于剪应力互等的双重等效条件推导得出；

57、所述基于应变能相等和基于剪应力互等的双重等效条件获取如下：

58、基于应变能相等的等效条件：

59、应变能等效是构建晶格弹簧模型弹簧键刚度与弹性常数之间的等效关系的基础条件；在张量形式的广义胡克定律表达式中考虑voigt对称性，推导获得应变能等效条件的通用显式表达式；

60、张量形式的广义胡克定律表达式为

61、

62、应用voigt对称性，有则式(12)可以重写为

63、

64、此外，工程常用的广义胡克定律表达式为

65、

66、比较式(13)和式(14)，可得

67、

68、式(15)即为应变能等效条件的通用表达式；

69、基于剪应力互等的等效条件：

70、剪应力互等的等效条件是确保晶格弹簧模型弹簧键刚度与弹性常数之间的等效关系构建准确的关键因素，前人都忽略了该等效条件的重要性；在张量形式的广义胡克定律表达式中剪应力互等恒成立，推导获得剪应力互等条件的通用显式表达式；

71、应用voigt对称性，有则由式(12)可得

72、

73、由剪应力互等条件可知，剪应力互等关于任意应变恒成立，即确保剪应力互等恒成立的条件可写为

74、

75、式(17)即为剪应力互等条件的通用表达式；

76、所述弹簧键的弹簧刚度与介质的宏观弹性常数之间的关系式推导如下：

77、基于应变能等效的推导：

78、控制体积中存储的平均应变能密度可以表达为

79、

80、式中，v为控制体积，nb为控制体积中包含的弹簧键数目，和分别为弹簧键b的法向刚度、切向刚度和法向-切向耦合刚度；此外，和分别为弹簧键b的法向和切向变形，可以表达为

81、

82、式中，l(b)是连接两个晶格颗粒的弹簧键b的长度，和分别为弹簧键b的法向应变和切向应变；考虑小转角情况(忽略旋转张量)，弹簧键b的法向应变和切向应变可以表达为

83、

84、式中，为弹簧键b的单位法向量分量，和是全局坐标系中的平均应变张量分量；

85、应用介质的宏观弹性张量与应变能密度的关系式介质的宏观弹性张量的各个分量可以表达为

86、

87、将式(21)代入等效条件式(15)和式(17)中，即可获得弹簧键刚度与宏观弹性常数之间的等效关系式(22)和(23)；其中，式(22)是基于应变能相等的等效条件推导而来，式(23)是基于剪应力互等的等效条件推导而来；

88、

89、

90、基于高斯散度定理的推导：

91、控制体积v中的平均应力可以表达为

92、

93、式中，σij是作用于整个控制体积内各点处的应力；

94、力学各向异性晶格弹簧模型中，介质行为由弹簧键网和晶格颗粒集组成的系统近似，应力只存在于晶格颗粒中；式(24)中的积分可以用控制体积v中包含的np个晶格颗粒的平均应力和代替；

95、

96、晶格颗粒p的平均应力也可以用式(24)表达为

97、

98、根据张量理论，任意张量sij满足表达式

99、sij＝δikskj＝xi,kskj＝(xiskj),k-xiskj,k  (27)

100、将式(27)应用于式(26)，得

101、

102、式中，两项积分分别用(iij)1和(iij)2表示；

103、根据高斯散度定理，第一项积分(iij)1中的体积分可以用面积分代替，则

104、

105、式中，s(p)为晶格颗粒p的表面，nk为垂直于晶格颗粒p表面s(p)向外的单位法向量，为作用在晶格颗粒p表面上的牵引力矢量；假设是连续可微的，如果忽略每个弹簧键承担的力矩，每个晶格颗粒都被作用在弹簧键位置处的点力加载，式(29)中的积分可以用求和代替为

106、

107、式中，为弹簧键b的中心位置，为弹簧键b作用在晶格颗粒p上的点力；弹簧键b的位置可以表示为

108、

109、式中，为晶格颗粒p的质心位置；将式(31)代入式(30)中，得

110、

111、在没有体力和外力的情况下，晶格颗粒p的运动方程为

112、

113、式中，ρ(p)为晶格颗粒p的密度，为晶格颗粒p的质心加速度，为作用在晶格颗粒p的质心处的合力；

114、基于式(33)，第二项积分(iij)2可以写成

115、

116、将式(32)和式(34)代入式(28)中，得

117、

118、由于作用在晶格颗粒p上的合力可以表达为

119、

120、式(35)中括号中的第一项和第三项相消，得

121、

122、使用式(37)时，晶格颗粒不必处于静止平衡状态，但不应该有体力和外力；

123、如果l(b)为弹簧键b的长度，为弹簧键b的单位法向量，为弹簧键b的内力，式(37)可以改写为

124、

125、将式(38)代入式(25)中，可得控制体积v中的平均应力为

126、

127、式中，弹簧键b的内力可以由其单位法向量法向力及切向力计算为

128、

129、此时，依次将式(40)、式(69)、式(19)及式(20)代入式(39)中，即可推得由平均应变表达的平均应力公式；最后，再应用介质的宏观弹性张量与平均应力的关系式即可推得介质的宏观弹性张量的各个分量表达式(21)，进而推得弹簧键刚度与宏观弹性常数之间的等效关系式(22)和(23)；

130、将三个弹簧键b1、b2和b3的弹簧刚度、单位法向量和长度代入式(22)和式(23)中，解方程组即得所述弹簧键的刚度参数转换式，如式(1)所示；

131、所述弹簧键的刚度参数叠加计算公式推导如下：

132、根据内力叠加，有

133、

134、式中，

135、根据变形协调，有

136、

137、式中，

138、根据胡克定律，有

139、

140、联立式(41)、式(42)、式(43)，化简可得弹簧键的刚度参数叠加计算公式，如式(2)所示。

141、其中，所述循环求解仿真模型核心步骤包括时间步长确定、运动定律、时间累积和力-位移定律；

142、所述运动定律阶段，计算位移和应变包括计算晶格颗粒的位移和应变；

143、力学各向异性晶格弹簧模型采用具有二阶精度的verlet显式时间积分方案求解晶格颗粒的完整动态方程，如式(44)所示，从而实现对介质变形破裂发展演化过程的准确模拟；

144、

145、式中，u是位移向量，m是对角质量矩阵，c是阻尼矩阵，k是刚度矩阵，f(t)是合外力向量；

146、晶格颗粒的速度和位移分别基于式(45)和式(46)更新；cundall提出的局部自适应阻尼能够使模型加速收敛到稳定状态解，力学各向异性晶格弹簧模型采用该阻尼方案求解准静态问题；局部自适应阻尼作用于每个晶格颗粒，并与不平衡力成正比，如式(45)所示；

147、

148、

149、式中，和分别是t时刻和t+δt时刻晶格颗粒p的位移，和分别是t-δt/2时刻和t+δt/2时刻晶格颗粒p的速度，是作用于晶格颗粒p上的合力，m(p)是晶格颗粒p的质量，δt为时间步长；此外，α是一个无量纲的局部阻尼系数，与力学性质和边界条件均无关；静态分析中，局部阻尼系数一般取值为0.7；动态分析中，局部阻尼系数一般取值为0或较小值；

150、力学各向异性晶格弹簧模型使用的求解方案是条件稳定的，时间步长必须保持在与整个系统的最小特征周期有关的临界值以下，以确保计算稳定性；对于各向同性模型，临界时间步长通常是基于弹性波穿过模型中最小单元所需的时间来估计的；然而，这种方法不适用于各向异性模型；在力学各向异性晶格弹簧模型中采用了potyondy提出的一种更通用的方法来估计临界时间步长；如果模型的自由度没有耦合，可以利用式(47)来估计临界时间步长；

151、

152、式中，m(p)是晶格颗粒p的质量，kij是晶格颗粒p周围弹簧键b的全局刚度矩阵；为了确保计算的绝对稳定性，最终的临界时间步长需要再乘以一个小于1的安全系数；

153、晶格颗粒p的平均应变增量可由其平均应变率累积为

154、

155、式中，为晶格颗粒p的平均应变率，δt为时间步长；

156、所述晶格颗粒p的平均应变率表达式推导如下：

157、在连续介质力学中，点处的应变是通过局部变形或位移计算出来的，具体来说是这些变形或位移的空间梯度；对于许多工程应用，一般可以假设应变很小，柯西的无穷小应变张量是适用的，此时应变可以计算为

158、

159、式中，εij(i＝x，y；j＝x，y)为应变张量，为位移梯度张量；

160、在一个封闭连续域上，连续位移场ui(xj)的位移梯度张量定义为

161、

162、为晶格颗粒p关联一个控制体积v(p)，则单位体积内的平均位移梯度张量可以表达为

163、

164、通过将高斯散度定理应用于晶格颗粒，体积积分可以用表面积分代替：

165、

166、式中，nj为垂直于控制体积表面s向外的单位法向量；

167、如果我们限制位移只发生在与晶格颗粒p关联的个弹簧键中，表面积分可以用求和代替；

168、

169、式中，是弹簧键b的位移，是弹簧键的单位法向量，a(b)是弹簧键的横截面积；

170、弹簧键b的位移可以由其直接连接的晶格颗粒p的位移表达为

171、

172、式中，是晶格颗粒p的位移；

173、将式(54)代入式(53)中，得

174、

175、根据高斯散度定理，矢量场在闭合曲面上的通量等于该矢量场散度在曲面内空间的体积分，有

176、

177、将式(56)代入式(55)中，得

178、

179、晶格颗粒p的平均位移梯度张量可以表达为

180、

181、将式(58)代入式(49)中，可得晶格颗粒p的平均应变表达式为

182、

183、将式(49)中的位移替换成速度，可得晶格颗粒p的平均应变率表达式为

184、

185、式中，为弹簧键b相对于其关联的晶格颗粒p的运动速度，实际计算中由晶格颗粒p周围直接连接的其他晶格颗粒p'相对于晶格颗粒p本身的运动速度表达为

186、

187、式中，为弹簧键b的中心点坐标，和分别为晶格颗粒p和p'的中心点坐标；

188、所述力-位移定律阶段，累积变形和内力包括累积弹簧键的变形和内力，判别失效并记录断裂包括判别弹簧键的失效并记录断裂位置和断裂模式；

189、具体的，力学各向异性晶格弹簧模型中的弹簧键两端产生伸缩或剪切变形，并基于胡克定律计算法向和切向内力；

190、弹簧键b变形向量可以由连接在两端的晶格颗粒pa和pb的位移向量计算得出，计算公式为

191、

192、式中，和分别是晶格颗粒pa和pb的位移向量；定义晶格颗粒从pa到pb的单位法向量为单位切向量为则弹簧键b的法向和切向变形向量可以计算为

193、

194、式中，如果弹簧键b伸长，弹簧键的法向变形向量是正的；如果弹簧键b逆时针旋转，弹簧键的切向变形向量是正的；

195、为了释放力学各向异性晶格弹簧模型可用泊松比的局限性，式(63)中的弹簧键的变形计算公式可以改写为

196、

197、

198、式中，和分别为弹簧键b的法向应变增量和切向应变增量，可根据式(20)计算为

199、

200、式中，为弹簧键b在全局坐标系中的各个平均应变增量，可以由其直接连接的晶格颗粒pa和pb的各个平均应变增量的体积加权平均计算为

201、

202、弹簧键b中的法向力由法向弹簧内力和法向-切向耦合弹簧内力组成，而弹簧键b中的切向力由切向弹簧内力和法向-切向耦合弹簧内力组成；如果使弹簧伸长的内力是正的，则可以计算出弹簧键b中力向量的法向分量和切向分量为

203、

204、写成矩阵形式为

205、

206、式中，是弹簧键b的法向弹簧刚度，是弹簧键b的切向弹簧刚度，是弹簧键b的法向-切向耦合弹簧刚度；

207、所述弹簧键的内力还包括弹簧键的应力，用于判别弹簧键的失效和断裂；

208、具体的，弹簧键b的应力取为连接的两个晶格颗粒pa和pb的局部应力的平均值，即

209、

210、对于任意晶格颗粒p，局部应力计算如下：

211、

212、式中，是晶格颗粒p周围弹簧键的数目，是晶格颗粒p的坐标，是晶格颗粒p周围弹簧键b的坐标，是晶格颗粒p周围弹簧键b的内力向量分量；此外，v(p)是晶格颗粒p的控制体积；

213、所述判别弹簧键的失效和断裂，通过将力学各向异性晶格弹簧模型弹簧键的主应力与相应强度准则比较实现；

214、具体的，力学各向异性晶格弹簧模型主要面向各向异性层状岩石的变形破裂计算需求开发，基于层状岩石适用的强度准则实现弹簧键的失效判别；各向异性层状岩石的强度通常和最大主应力σ1方向与岩石结构面或层理面倾向的夹角β相关；

215、判别式定义如下：

216、d1拉伸失效判别式

217、ft(β)＝-σ3-σt(β)  (72)

218、式中，σt(β)为岩石结构面或层理面倾向与最大主应力σ1方向的夹角呈β时的岩石抗拉强度；

219、d2剪切失效判别式

220、fs(β)＝(σ1-σ3)-s1(β)  (73)

221、式中，s1(β)＝σ1(β)-σ3为岩石结构面或层理面倾向与最大主应力方向的夹角呈β时的岩石主偏应力强度，

222、利用上述判别式，可以直接判别弹簧键的失效状态和失效模式；具体地，当ft(β)≥0时，弹簧键拉伸失效；否则，当fs(β)≥0时，弹簧键剪切失效；

223、各向异性层状岩石的剪切失效通常包含两种不同的失效模式：一种是滑动模式，失效是由沿结构面或层理面的滑动引起的；另一种是非滑动模式，失效由岩石材料控制，不依赖于结构面或层理面；判别式中应用具体的剪切失效准则时需要进行区分；

224、c1弹簧键拉伸失效准则

225、

226、式中，σt(β)为岩石结构面或层理面倾向与最大主应力σ1方向的夹角呈β时的抗拉强度，σt(0°)和σt(90°)分别为其对应β＝0°和90°时的值；

227、实际应用中，岩石基体和岩石结构面或层理上的弹簧键都需要通过该拉伸失效准则判别是否发生拉伸破坏；此外，通常将该准则作为剪切失效准则的拉伸截止条件；

228、c2弹簧键剪切失效准则

229、c21岩石结构面或层理面上的滑动失效准则

230、岩石结构面或层理面上的滑动失效表达式为

231、

232、式中，

233、

234、其中，c0j和φ0j分别为低围压(围压趋于0)三轴试验环境下使最大主应力σ1方向与岩石结构面或层理面的夹角呈β时获得的对应于线性莫尔-库仑强度准则的粘聚力和内摩擦角，实际应用中需满足0<β<90°-φ0j；此外，σ3为最小主应力，σcrt为岩石的临界围压(critical confining pressure)，与岩石基体和结构面或层理面的性质有关；

235、c22岩石基体及结构面或层理面上的非滑动失效准则

236、表达式为

237、

238、式中，s1(β)＝σ1(β)-σ3为弹簧键的主偏应力，β为σ1(β)与岩石结构面或层理面倾向的夹角，n为岩石的各向异性指数，与岩石弹性常数有关，k为对应于β＝0°和90°时的主偏应力比

239、k＝s1(0°)/s1(90°)  (78)

240、其中，s1(0°)和s1(90°)共用强度包络线，表达式为

241、

242、式中,

243、

244、其中，c0(β)和φ0(β)分别为低围压(围压趋于0)三轴试验环境下使最大主应力σ1方向与岩石结构面或层理面的夹角呈β时获得的对应于线性莫尔-库仑强度准则的粘聚力和内摩擦角，计算s1(0°)和s1(90°)时分别取β＝0°和β＝90°；此外，σ3为最小主应力，σcrt为岩石的临界围压，与岩石基体和结构面或层理面的性质有关；

245、c23结构面或层理面上的弹簧键失效后的滑动准则

246、sjm仅用于结构面或层理面上的弹簧键失效后的滑动计算；模型计算前，预定义一组可能发生滑动失效的潜在不连续面，但先不将其用于修改与之相交的弹簧键的内力计算方式；相反，计算过程中每个循环步都使用上节介绍的失效准则检查与这些潜在不连续面相交的弹簧键的状态，以区分滑动失效和非滑动失效；当弹簧键发生滑动失效时，将潜在不连续面用于修改弹簧键的内力计算方式，即配置sjm及相关参数，此时弹簧键的局部方向系统将与潜在不连续面的方向对齐；当弹簧键发生非滑动失效时，则保持其原有的内力计算方式，仅将法向-切向耦合刚度设置为0；对于所有未被潜在不连续面穿过的其他弹簧键，计算过程中只检查非滑动失效模式；

247、此外，对于任何弹簧键，都要首先检查是否发生拉伸失效；对于任何一种失效模式，都假定残余强度为零；弹簧键失效的同时记录断裂位置及断裂模式。

248、其中，所述实施结束条件判断并继续或终止仿真模型循环求解涉及准静态问题仿真和动态问题仿真的结束条件判断和循环求解；

249、具体的，当所述循环求解为准静态问题仿真时，计算晶格颗粒的位移和应变，累积弹簧键的变形和内力，判别弹簧键的失效并记录断裂位置和断裂模式，将系统动能或不平衡力作为结束判别条件，当所述结束判别条件小于等于目标值时，终止仿真模型循环求解；

250、当所述循环求解为动态问题仿真时，计算晶格颗粒的位移和应变，累积弹簧键的变形和内力，判别弹簧键的失效并记录断裂位置和断裂模式，将仿真物理时间作为结束判别条件，当所述结束判别条件大于等于目标值时，终止仿真模型循环求解。

251、本发明的一种材料变形破裂的力学各向异性晶格弹簧模型(m-alsm，mechanicalanisotropic lattice spring model)仿真方法，融合了宏观连续方法和细观非连续方法的诸多优势，能够在一个统一的框架下自然地模拟材料的变形、断裂和破碎等任意简单或复杂的力学问题，能够通过简单地打断弹簧模拟复杂的裂纹动态扩展问题，从而避免传统计算方法处理非连续力学问题在数学上遇到的限制和困难，且具备以下优点：直接利用宏观本构参数、无需校准层理本构参数、单元尺度上的弹性均匀性、模拟多重复杂断裂的能力、处理复杂边界条件的能力、模拟多尺度问题的能力、模拟多物理场的能力以及高计算效率。基于上述优点，本发明为各向异性材料的变形、断裂和破碎行为分析提供了新方法、新工具、新选择，尤其在层状岩石破裂模拟方面具有巨大潜力。

252、本发明主要做出了以下几点创新贡献：

253、(1)同时使用法向弹簧、切向弹簧和法向-切向耦合弹簧构建了描述晶格颗粒间相互作用的新型弹簧键，克服了非耦合刚度矩阵表达层状岩石复杂各向异性变形不准确的问题，一定程度上释放了模型可用泊松比的限制；

254、(2)使用基于应变能相等和基于剪应力互等的双重等效条件，利用两种不同方法(基于应变能等效的方法和基于高斯散度定理的方法)严格推导了弹簧刚度与介质宏观弹性常数匹配的关系式，使所发明的各向异性晶格弹簧模型能够简单直接地用于各向异性材料的变形破裂计算分析；

255、(3)基于高斯散度定理严格推导了晶格颗粒平均应变计算公式，定义了弹簧键平均应变计算方法，利用弹簧键平均应变计算弹簧键变形替换晶格颗粒相对位移计算弹簧键变形，消除了现有晶格弹簧模型描述不同材料泊松比多样性的可用泊松比分布的局限性，使所发明的各向异性晶格弹簧模型能够对任意材料的理论泊松比分布实现全覆盖；

256、(4)创新地将nova-zaninetti准则(nova and zaninetti,1990)和asadi和bagheripour(asadi and bagheripour,2015)准则相结合，实现了层状岩石层理和基体的拉伸和剪切破坏的统一描述，在层状岩石层理和基体的性质无限趋于相同时，使两者的破坏条件自然地统一到一起。

257、需要强调的是，本发明做出的上述几点创新贡献是通用的，可以很方便地移植到其他数值方法中。