一种预测公交车到站时间的方法与流程

本发明涉及交通技术领域，更具体地，涉及预测公交车到站时间的方法。

背景技术：

随着我国城市化进程的发展，城市的经济得到了发展，人口、车辆也大量增加，随之引发了一系列的交通问题，尤其是交通拥堵。公共交通具有承载率高、污染小、运输效率高等特点，故大力发展公共交通可以减缓城市拥堵现象。近年来，智能交通得到了重视和发展，出行者对于公交车到站时间的获取需求也日益增加。到站时间公开之后，乘客可以提前规划行程。这将吸引他们选择公共交通出行，从而缓解交通压力。此外，公交运营公司的可以根据公交车的到站时间进行调度，有利于公交管理向动态智能化的转变，提高运营效率。

公交到站时间预测近年来在国内外都引起了广泛关注。例如，都柏林在站点设置了电子站牌来展示到站时间；在日本，公交车到达时间预测是政府大力支持的一项交通需求管理措施。通过互联网向用户的手机和电脑发送公交车的预测到达时间吸引人们乘坐公交车出行，从而限制私家车使用数量。在中国的应用主要分为两种：一种是布置实体公交电子站牌，例如上海在站牌上展示公交到站时间；另外一种是利用客户端软件发布信息。用户可以通过这些软件获取公交车的位置(距离)信息等。

目前虽然存在多种预测模型，如基于历史数据、人工神经网络、支持向量机等，但是基本上预测精度有限。公交车的行驶过程受到各种随机因素的影响，尤其我国城市交通环境复杂，目前已有的成熟预测方法得到的公交到站时间不够准确，可靠性较低。总体看来，关于公交车到达时间预测技术的研究仍然较少或者存在一定的局限性，亟待开发一种新型的公交到站时间预测方法。

技术实现要素：

本发明提供一种克服上述问题或者至少部分地解决上述问题的预测公交车到站时间的方法。

根据本发明的一个方面，提供一种预测公交车到站时间的方法，其特征在于，包括：

S1、采集一定时间内的公交车数据以及公交线路数据，基于空间插值法，获得公交车在各数据点的时距数据对；

S2、基于所述时距数据对，获得公交车运营序列；

S3、将所述公交车运营序列输入至LSTM递归神经网络，获得公交车到站时间预测模型；以及

S4、对所述公交车到站时间预测模型基于链式预测法，获得预测的公交车到站时间。

本发明提出利用递归神经网络进行公交到站时间预测的方法：利用我国城市公交在运营时的公交车数据和公交线路数据，提取与交通相关的信息，经过训练LSTM递归神经网络，学习交通状况变化的规律，从而得到公交车在动态变化交通环境下的到站时间。

附图说明

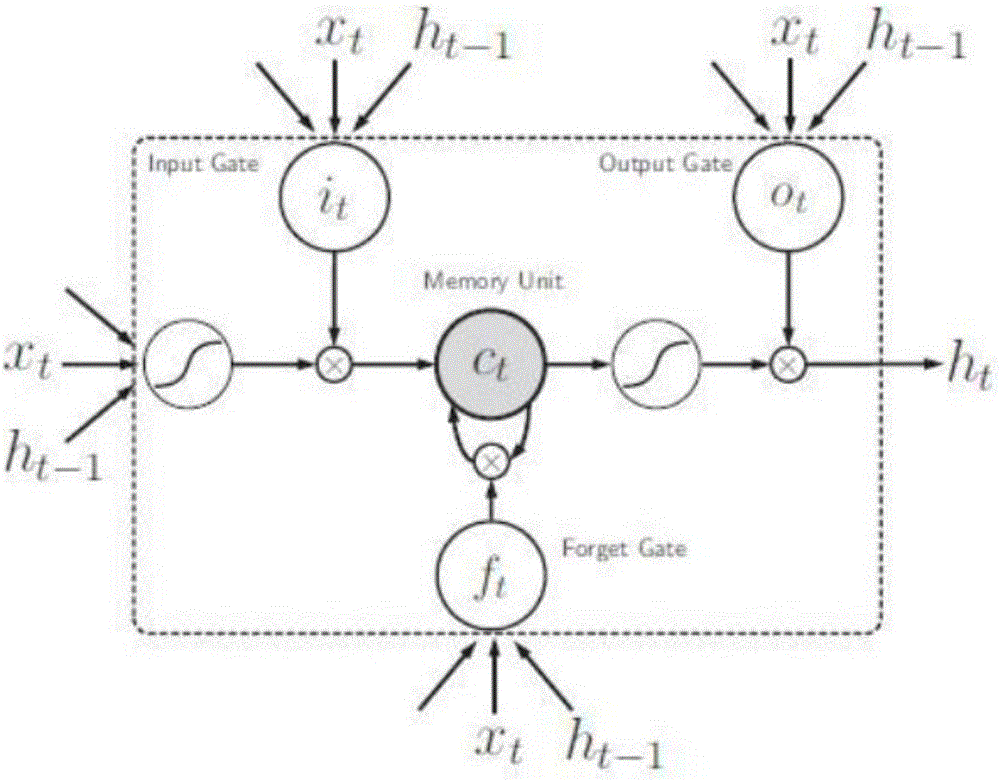
图1为本发明实施例中LSTM型RNN中隐藏层结点的结构图；

图2为根据本发明实施例的预测公交车到站时间的流程示意图；

图3为根据本发明实施例的计算除首站之外站点的出发时间的一维线性回归示意图；

图4为根据本发明实施例的预测到站时间结果说明图；

图5为根据本发明实施例的预测方法与其他4种方法的结构图。

具体实施方式

下面结合附图和实施例，对本发明的具体实施方式作进一步详细描述。以下实施例用于说明本发明，但不用来限制本发明的范围。

为了克服现有预测方法存在的公交到站时间不够准确、可靠性交底的计算问题，本发明提供了一种基于LSTM递归神经网络的预测公交车到站时间的方法。下面结合附图对本发明的具体实施方式进行说明。

递归神经网络(Recurrent Neural Network，RNN)通过添加自连接隐藏层，赋予神经网络对时间进行建模的能力，从而区别于其他的神经网络。RNN隐藏层的输出，不仅仅会传播到下一层，而且还进入了下一时刻的本隐藏层，但RNN会受到梯度消失或梯度爆炸的影响，导致它难以学习较远时间点对当前时间点的影响。本发明采用具有解决上下文长时间依赖的RNN网络结构，如长短时神经网络(Long Short Term Memory，LSTM)，带门结构的递归单元神经网络(Gated Recurrent Unit，GRU)等。

本发明采用的RNN为LSTM型RNN，通过将普通的神经元用带有门结构(在本发明中，包括输入门、遗忘门和输出门)的记忆单元(Memory Cell)替换，解决了梯度消失或梯度爆炸的问题。在前向传播中，门结构控制了激活的进入和输出；在后向传播中，门结构控制了残差的流入和流出。如图1所示，此为带有一个记忆单元的隐藏层神经元结点，包含三个门：输入门i、遗忘门f和输出门O，i_t，f_t，o_t分别是三个门在时刻t对应的激活值；x_t和h_t-1是神经元输入数据的两个来源，其中x_t是上一层的神经元在t时刻的输出，而h_t-1是上一个时刻即t-1时刻本层所有神经元的输出值；C_t是内部状态在此时刻的值；h_t是当前t时刻隐藏结点的输出值。它们的计算过程为：

i_t＝σ(W_xi*x_t+W_hi*h_t-1+b_i)；

f_t＝σ(W_xf*x_t+W_hf*h_t-1+b_f)；

o_t＝σ(W_xo*x_t+W_ho*h_t-1+b_o)；

C_t＝f_tοh_t-1+i_tοg_t；

其中W_xg，W_xi，W_xf，W_xo，W_hg，W_hf分别是连接各层(不同结构)的边的权值；b_i，b_f，b_o，b_g是偏置项，权值和偏置项都是待求参数。在RNN中，权值和偏置项在不同的时刻共享相同的值。σ和是不同的激活函数，σ常为Sigmoid函数，而可以为tanh函数或tanh函数的变种。ο运算符代表元素对应相乘。

利用LSTM能够学习长期依赖关系的特点，本发明从已有的定位数据和静态数据中提取在公交到站预测问题中LSTM所需的时间序列信息，用这些信息反映描述某时间某位置的交通状况。本发明将时间序列信息输入至网络中以学习交通状态，并用LSTM记忆单元的内部状态进行存储。隐藏层节点的输出经过前向传播过程，直到网络的输出层，通过预测到站时间。故本发明预测的公交到站时间是基于动态变化的交通状态的，更具有可靠性。

图2示出了本发明的流程示意图，包括：

S1、采集一定时间内的公交车数据以及公交线路数据，基于空间插值法，获得公交车在各数据点的时距数据对；

S2、基于所述时距数据对，获得公交车运营序列；

S3、将所述公交车运营序列输入至LSTM递归神经网络，获得公交车到站时间预测模型；以及

S4、对所述公交车到站时间预测模型基于链式预测法，获得预测的公交车到站时间。

本发明提出利用递归神经网络进行公交到站时间预测的方法：利用我国城市公交在运营时的公交车数据和公交线路数据，提取与交通相关的信息，经过训练LSTM递归神经网络，学习交通状况变化的规律，从而得到公交车在动态变化交通环境下的到站时间。

本发明所述的公交车数据包括：公交车编号、公交车所属线路的线路编号、公交车的地理位置数据、公交车的地理位置数据的采集时间、运营次数以及上下行方向，其中公交车的地理位置数据为公交车在运营过程中通过车载定位系统发射的全球定位系统(Global Positioning System，GPS)数据。

本发明所述的公交线路数据包括：公交线路的线路编号、线路中各站点编号、各站点的地理位置数据、各路口的地理位置信息以及上下行方向。之所以选择路口，是因为交通受到信号灯的控制影响较大，主要体现在信号灯的改变会引发交通状态的突然变化，从而影响公交车的运行时间，比如由绿灯变换成红灯之后，交通流被截断，处于被截断部分交通流的公交车会增加停车延误时间以及引道延误时间。

由于公交线路数据和公交车数据通常保存在公交公司的数据库中，数据的组织形式是杂乱无章的，本发明首先需要将属于公交车不同次运营的定位数据区分开来，使每一个划分出来的小集合里的数据都属于同一次运营。

具体地说，所述步骤S1包括：

S1.1、采集一定时间内的公交车数据以及公交线路数据，获得对应不同线路、不同运营次数的公交车的历史时距数据信息，所述历史时距数据信息包括所述线路的首站点和末站点的地理位置数据、线路总距离和总到站时间。

获得公交车的历史时距数据信息的方法属于现有技术，例如，可以采用专利“一种公交时距数据的获取方法及服务器”(发明号：2016108876465)的方法获得，

在到站预测问题中，我们还需要知道公交车到达各个站点的时间，因此，步骤S1还包括步骤S1.2：基于所述历史时距数据信息，通过空间插值法，获得各数据点的积累距离。

所述步骤S1.2具体包括：根据线路编号和上下行标志，我们从数据表里查询线路的中间站点和沿线路的路口的经纬度位置。通过空间插值，如克里金插值法得到站点(也可以是路口，下同)的累积距离：设某次运营的定位数据的坐标值为x₁，x₂，...，x_n，对应的观测值为计算得到的累积距离Z(x₁)，Z(x₂)，...，Z(x_n)，所述积累距离为该站点到首站点的距离，那么对于某个站点(路口)的经纬度坐标x₀，它对应的累积距离Z(x₀)可以用线性组合来估计，其中λ_i为组合权重，体现了x₀与x₁，x₂，...，x_n之间的关系，该关系通过求解克里金方程得到，由于篇幅问题，求解克里金方程的方法不再详细说明，可参考论文Oliver,M.A."Kriging:A Method of Interpolation for Geographical Information Systems."International Journal of Geographic Information Systems 4:313–332.1990。

在得到中间站点的累积距离之后，我们通过线性回归的方法计算公交车的到达除首站之外各站点的时间。根据已知的输入，输出数据(在该问题中，输入和输出分别为定位数据的连续累积距离和采集时间)，拟合线性函数(在该问题中，为连续累积距离和采集时间的关系表示)，并将未知的数据输入(在该问题中，为站点的累积距离)至拟合的函数中，得到所需要的值(在该问题中，为到达站点的时间)。具体的操作过程如下：

图3示出了计算各站到达时间的线性回归示意图，如图3所示，黑色的点表示的是根据专利“一种公交时距数据的获取方法及服务器”(发明号：2016108876465)获得的各定位数据的连续累积距离以及采集时间，蓝色的线是拟合函数，该拟合函数的过程通过python计算机程序语言中的sklearn.linear_model包来实现，具体的程序如下：

regr＝linear_model.LinearRegression()

regr.fit(X,Y)

y_pred＝regr.predict(x)

其中，第一个语句得到函数句柄，第二个语句输入已知的输入数据X和输出数据Y，得到拟合函数；第三个语句输入数据X至拟合函数中，计算得到y_pred，其中输入数据X对应于公交车辆实时动态位置对应的累积距离；输出数据Y对应于公交车辆实时动态位置所在的数据采集绝对时间，x是除去首站之外的各站点的累积距离，得到的y_pred即所需的各站到达时间。

进一步地，由于公交车在30秒时间间隔内的运营距离会较长，本发明对每百米距离的位置进行采样，作为采样点，通过线性插值，得到对应的公交车运行时间。

插值的目的是为了改善车载定位装置低频率发射定位数据的缺点，使模型能够以更高频率监测交通状态的变化和公交车的运行情况。

在得到各数据点的积累距离后，本发明的步骤S1还包括步骤S1.3，将所述积累距离和对应的到站时间作为公交车到达该数据点时的时距数据对。

在一个实施例中，时距数据对相应的来源可能是站点、采样点或者路口点。一次运营过程中，按时间顺序排列的所有时距数据对记录了公交车在时间和空间范围内的移动情况。

在一个实施例中，本发明在获得所有时距数据对后，开始构建时间序列，以训练LSTM模型，在公交车到站时间预测问题中，公交车运营序列(或简称为运营序列)是“时间序列”。

本发明中的所述步骤S2具体包括：

S2.1、将公交车到达各数据点时的时距数据对、当前数据点与下一数据点的间距、共享同一个站点的线路总数以及数据标识符作为特征向量，构成对应各数据点的公交车运营特征向量。

具体来说，一次运营中的所有时距数据对的序列记为S＝(S₁，S₂，...，S_i，...S_N)，其中S_i＝(t_i，d_i)^T，记录了公交车到达S_i对应位置的运行时间t_i和积累距离d_i。以S_i为例，计算LSTM所需的部分输入信息，包括：当前时刻T_i＝t_i+ST，其中，ST是公交车离开第一个站点的绝对时间，当前位置和首站之前的距离以及和下一个数据点的间隔距离Δd_i＝d_i+1-d_i。

通过对数据库的查询得到共享同一个站点的线路总数量(li，当第i个数据点不对应站点时，值为0)；给予每一个数据点一个one-hot向量(f_i，即一位有效编码)以区分不同来源的数据点，如：当数据点为站点时，f_i＝[0，0，1]；当为采样点时，f_i＝[0，1，0]；当为公交车的地理位置时f_i＝[1，0，0]。这五种特征构成了一个公交时距数据对的运营特征向量，X_i＝(T_i，d_i，Δd_i，l_i，f_i)^T。

由此可知，运营特征向量的每个特征都是和交通状态密切相关的：T_i和d_i分别为当前时刻(用绝对时间表示)和公交车所处的当前位置(用和首站之间的距离表示)，这将告诉网络需要学习何时何地的交通状态；Δd_i是待预测位置和当前位置之间的距离，这明确了需要预测多远距离内的交通变化情况；l_i特指共享站点的线路数量，用来反映站点的承载力对公交车运营的影响：线路数量的多少关系到上进出站的排队长度，从而影响上下车的延误时间。在这样的输入条件下，本发明让LSTM网络学习在某时空条件限定下的交通状态以及在一定距离范围内交通的逐渐变化情况。在此期间若遇到信号灯路口等特殊位置，网络还需要考虑交通突然变化的可能性。

运营序列作为LSTM的输入，它对应的目标输出是公交车到达下一个位置点的运行时间，即对X_i来说，对应的目标输出Y_i＝t_i+1。目标序列记为Y＝(Y₁，Y₂，...，Y_i，...Y_N-1)。线路所有的运营序列(X₁，X₂，...，X_M)和对应的目标序列(Y₁，Y₂，...，Y_M)构成运营序列训练集，其中M是此线路公交车运营的总次数。

在获得公交车运营特征向量后，所述步骤S2进一步包括步骤S2.2：对所述公交车运营特征向量中除数据标识符外的各特征向量依次进行归一化处理(除以各特征的最大值maxV)和去均值处理(减去各特征的均值meanV)，获得所述公交车运营序列。

在一个实施例中，所述步骤S3进一步包括：

基于所述公交车运营特征向量的维度，对所述公交车运营序列进行分批，获得若干批数据。

具体地说，LSTM的输入为K维向量，K即公交运营序列特征向量的维度(即特征向量的长度)。本发明将公交车运营序列进行分批：设定一个miniBatch值，例如可设定为256，将运营序列训练集共分为(M/miniBatch)批。

对每一批数据来说，在公交车到达每一个数据点的时刻向LSTM递归神经网络输入该批数据对应的公交运营序列(miniBatch×K×1的矩阵)，经前向传播，所述LSTM递归神经网络存储交通状态，并输出网络输出值。

接下来比较所述网络输出值和此时刻的目标输出值，获得均方误差，作为LSTM网络的误差，同时使用时间展开的后向传播计算并传递残差，对所有批的数据完成一次前向和后向传播的过程称为一次迭代，经多次迭代(可以预先设定一个值，也可以当误差小于某个设定的值后停止迭代)，获得所述公交车到站时间预测模型。

在一个实施例中，基于随机梯度下降法(Stochastic gradient descent,SGD)，对LSTM递归神经网络中的权值和偏置进行更新。具体的更新方程为：

new W_xi＝W_xi+(m*W_xi-αΔW_xi)

new b_i＝b_i+(m*b_i-αΔb_i)

其余的权重和偏置的更新方程与上述公式类似。其中α是学习率，m是冲量因子，它的引入有助于训练过程中更新的权重和偏置陷入局部最小值。

在本发明中，预测公交车到站时间的过程定义为“无输入的链式预测”，所述步骤S4包括：

S4.1、将公交车的当前位置到预测位置之间的其他数据点作为辅助点。具体地说，假设线路共有n个站点，公交车当前正位于第i个站点(记为当前站点，i＝1，...，n-1)，想要预测到达下游目标站点(记为第j个站点，j＝i+1，...，n)的时间。预测过程按照i-＞a_p1-＞...-＞a_pn-＞j的顺序展开，其中a_p1，...，a_pn是两个站点之间存在其他的位置点(如两个站点之间的采样点、路口点)，我们将它们统称为辅助点。

S4.2、向所述公交车到站时间预测模型输入基于当前位置计算的公交车运营特征向量，经前向传播获得公交车运行至第一个辅助点的预测的到站时间。具体地说，根据当前站点的时距数据对S_i计算对应的运营特征向量X_i，输入至训练好的LSTM网络中，经过前向传播过程得到的输出值，即网络预测公交车运行至a_p1的时间，记为O_p1。

我们继续预测公交车从a_p1运行至a_p2的时间，由于车辆还未到达a_p1所处的位置，所以，a_p1对应的运营特征向量中的时间特征需要用上一步的预测结果来替代，即a_p1对应的运营特征向量X_p1＝(T_p1D_p1，Δd_p1，l_p1，f_p1)^T＝(O_p1，D_p1，Δd_p1，l_p1，f_p1)^T(除了当前时刻特征是用上一步的预测结果替换之外，其余特征都跟网络输出结果无关，可以从数据库查询得到或者计算得到)。

S4.3、将所述预测的到站时间将作为下一辅助点对应的到站时间，结合其余特征向量，构成下一辅助点的公交车运营特征向量，重复步骤S4.2，直至获得预测位置的网络输出值；以及

S4.4、对所述步骤S4.3的网络输出值进行反去均值(加上S2.2步骤中得到的各特征的平均值meanV)和反归一化(乘以S2.2步骤中得到的各特征的最大值maxV)处理，获得预测的公交车到站时间。

当车辆位于第i个站点，下游的交通状态都是预测得到的。随着车辆的向前移动，如真正到达第i+1个站点后，我们才可以得到真实的运营特征向量。将该向量再输入至LSTM网络中纠正历史预测的交通状态，再次预测第i+1个站点的下游目标站点到站时间(这里的时间指当前时间减去公交车离开首站的时间得到的时间)。因此，对一次运营来说，预测结果是一个下三角矩阵，如图5所示，横坐标(水平方向)代表当前站点，纵坐标代表下游站点，则第列的含义代表公交车当前位于第个站点时预测到达下游各站点的时间。所以，图4的矩阵包括以下含义，1、此线路共有十个站点；2、矩阵第t列(1≤t≤9)的含义为：当公交车到达第t个站点时，模型预测公交车到达第t+1个站点至第十个站点的时间。

下面给出本发明的的应用实例：

以北京118路(紫竹院南门—红庙路口东)为例用本发明进行预测，并和其他方法进行比较。对比的方法是Sinn,M.,Ji,W.Y.,Calabrese,F.,&Bouillet,E.(2012).Predicting arrival times of buses using real-time GPS measurements.(Vol.24,pp.1227-1232)。对比文件中提到的四种方法，分别为：基于延迟的预测(，Delay-based Prediction，DB)，线性回归(Linear Regression，LR)，K近邻(K-Nearest Neighbor，KNN)和核回归(Kernel Regression，KR)。

以在2015年2月份采集的该线路的定位数据为基础进行到站时间预测。将前27天的数据(共704条公交车运营序列)作为训练数据，预测2月28日共Y(Y＝31)次运营的到站时间。并用平均绝对误差(mean absolute error，MAE)评估预测结果：

我们使用的LSTM模型包含一个输入层，一个共有64个隐藏节点的隐藏层以及一个单一的线性输出单元。记忆单元的激活函数为tanh函数。值域在[0，1]之间的sigmoid函数是三个门的激活函数。权值用高斯分布进行初始化，使其服从N(0，1/(N_in+N_out)，其中N_in和N_out分别指前一层和当前层的神经元数量。SGD方法的冲量因子设置为0.95，学习率在迭代中保持不变为0.0001。

五种方法得到结果如图5所示。对所有预测长度的平均误差而言，LSTM方法比其余四种方法中的最好结果提高了约24秒。在现实生活中，公交线路所在的道路上一般不会只有一辆公交车，所以短距离的预测是更贴近现实的。我们统计短距离预测的预测结果，预测距离为一站到五站，对应图5的第三到第七行。当预测距离为一站时，预测公交车到达下一个站点的时间；当预测距离为两站时，预测公交车到达下游两个站点的时间，依此类推。注意，预测距离为所有站点时，则是预测公交车到达所有下游站点的时间。可以看到，LSTM的无论是长距离预测还是短距离预测，结果都是优于其他方法的。

综上所述，本发明提供了一种利用递归神经网络预测公交到站时间的方法。利用RNN来学习交通状态的变化，将公交到站时间和交通情况关联起来，得到更为可靠精确的预测结果。总的来说，用LSTM型RNN预测公交车到站时间具有以下的特点：

1.LSTM模型具有长时记忆历史信息的优点。因为交通的变化也具有历史相关性，上下游的交通情况是互相影响的，故我们用记忆单元来存储交通状态，并且利用记忆单元的内部状态随时间展开而变化的模式来模拟交通状态的演变。LSTM网络的输出在本问题中定义为预测的到站时间，故得到的公交到站时间是基于交通状态的，相对于其它方法是更值得信任的。

2.LSTM模型具有很好的扩展性。对于其他模型来说，加入多元信息很困难，而我们可以不断地加入更多和交通相关的特征到LSTM模型中。在目前已有数据的基础上我们只提取了五类特征。然而，交通还受到很多其他动态因素的影响，如天气等。如果在未来能得到更多的信息，我们需要做的只是对数据进行处理得到新的特征，并增加LSTM网络的输入或者输出维度。更多重要影响因素的加入可能会进一步提高预测的准确性。

3.LSTM模型不用限制序列的长度，故我们可将到站预测扩展为预测任意地点的公交车到达时间(适用于某些城市挥手即停的模式)。我们只需要对任意想要预测的位置进行插值，经过计算得到对应的运营特征向量，加入已有的序列中，再利用训练好的模型进行链式预测即可。

最后，本发明的方法仅为较佳的实施方案，并非用于限定本发明的保护范围。凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。