构型能量计算和晶体结构预测

1.本发明涉及用于确定系统的晶体结构的方法或计算系统的构型能量的方法，特别是计算具有多个粒子的系统的构型能量的方法。


背景技术：

2.晶体结构预测(csp)在理解材料的行为方面是基本的。晶体结构的精确知识允许计算材料在不同环境条件下的物理和化学性质。后者开启了设计材料以适应广泛应用的可能性，包括用于基于结构化的药物设计或生物材料基因组学。
3.csp可以被认为是一个优化问题，其中该系统的焓是待优化的量；最稳定的晶体结构是具有最小焓的晶体结构。如x射线衍射的试验方法通常用于表征晶体结构，但是不能用于预测它本身。另外，在一些情况下，试验数据可能无法确定晶体结构。例如，这可能是由于当经受高压或高温时有缺陷的样品，并且在此类情况下，理论方法提供了预测晶体结构的唯一解决方案(例如，使试验确定更困难的危险的或有毒的环境)。
4.真实的晶体包含太多分子以至于不能真实地模拟。然而，幸运的是，存在许多良好建立的、可以用于具有周期性边界条件的系统的模拟方法。此类方法搜索系统的相对于在一个模拟晶胞中的坐标的焓最小值，假设坐标然后被复制以描述无限晶体。因此，一般方法是使用优化算法，其搜索一个模拟晶胞内的核坐标的构型空间，试图定位具有最低焓的结构。
5.为了预测晶体结构，经常采用局部优化方法，迭代晶体结构以找到能量最小值。然而，最小值的数量随着系统大小而显著增加，并且对于甚至中等大小的系统，通常存在太多的最小值，从而没有使用这样的局部优化方法来定位最低最小值的实际机会。因此，已经对更多
‘
全局’优化方法进行了许多研究，其尝试使用策略不仅定位局部最小值，而且更智能地搜索空间中最低最小值，并且在最佳情况下，定位全局最小值。
6.对于csp存在许多计算技术，但是就定位全局晶体结构最小值的通用性和广泛性而言，它们都不倾向于匹配盆地跳跃(bh)。然而，这种技术通常需要输入一些外部数据，例如以试验得到的晶格向量或密度的形式。更重要的是，当应用于具有非常小的单胞(unit cell)(或模拟晶胞)的材料时，用此类常规技术预测晶体结构变得有问题。将此技术应用于此类材料常常导致粒子之间相互作用的非静电部分的截断，从而导致结果不准确。一个解决方案将是定义足够大的模拟晶胞，然而，由于最小值的数量随着系统大小而显著增加，所以计算成本将显著增加。
7.在常规模拟方法中，定义结晶固体中的粒子间的非静电相互作用电势截止距离的截止半径被限制于晶体结构的单胞(即，模拟晶胞)。这需要与通常用于具有周期性边界条件的系统的最小图像惯例一致。
8.然而，对于具有非常小的单胞的晶体系统，截止半径通常太小以致不能适当地考虑导致不准确结果的非静电势能相互作用。该问题的解决方案将是增加模拟晶胞的尺寸到超出单胞。然而，由于局部能量最小值的数目随着系统大小而大幅度增加，所以定位全局最
小值所需的计算能力将显著增加。
9.本发明旨在通过提供一种用于预测具有任意尺寸的单胞的材料的晶体结构但不显著增加计算成本的方法来至少改善上述缺点。


技术实现要素：

10.根据本发明的第一方面，提供了一种用于计算具有多个粒子的周期性边界条件的系统的构型能量的计算机实现的方法，所述方法包括以下步骤：i)定义截止半径，所述半径定义该系统中的粒子间的非静电相互作用电势截止距离；ii)定义一组晶胞向量以生成模拟晶胞；iii)定义一组超晶胞向量以生成超晶胞，其中所述超晶胞包括模拟晶胞的多个副本；对于位于该超晶胞内的每个粒子，计算该粒子与该截止半径内的任何和所有另外的粒子间的非静电对势，所述非静电对势由该粒子与位于该截止半径内的任何和所有其他粒子的相互作用产生；以及v)将所有这些不同的非静电对势求和以提供该系统的非静电构型能量。
11.本发明允许通过去除模拟晶胞尺寸等于或小于晶体结构的单胞的约束，而确定具有任意尺寸的单胞的系统的晶体结构。本发明通过使用超晶胞扩展方法克服了这个问题，允许使用不受限制的截止半径来准确地确定系统的总焓，该系统具有以任意单胞尺寸布置在晶体结构中的多个粒子。因此，本发明提供了一种更有效的方法来定位对应于稳定的晶体结构的构型能量的全局最小值。
12.这种晶体结构确定的应用包括药物应用(如上所述)、矿物学、晶体学和晶体工程(仅举几例)。如上所述，通过确定(稳定的)晶体结构，可以指导试验工作。
13.可以理解，可以对任何系统施加周期性的边界条件，而不管系统是否是晶体状的。例如，这些系统可包括非晶形固体和液体。
14.在一个实施例中，在部分iv)的方法中，粒子的非静电对势可以包括位于超晶胞外但在截止半径内的粒子。
15.此外，或可替代地，步骤iv)可以使用标准最小图像惯例考虑围绕粒子的另外的图像粒子来选择由粒子与位于超晶胞内和/或外的最近粒子或图像粒子的相互作用产生的所述非静电对势。这确保了在计算非静电对势时(仅)考虑最近的图像。
16.根据本公开的实施例，计算步骤iv)可还包括以下步骤：对于位于所选择的模拟晶胞内的每个粒子，计算该粒子与在截止半径内围绕该粒子的任何和所有另外粒子间的非静电对势。
17.此外，该求和步骤v)可以包括以下步骤：对所选择的模拟晶胞内的每个粒子的不同的非静电对势进行求和；以及将该和乘以超晶胞内的模拟晶胞的数量，以获得构型能量，并且其中该构型能量是该系统的每超晶胞的非静电势能。
18.该方法的步骤可以包括计算所选的模拟晶胞内的每个粒子的非静电对势。如果截止半径延伸超过所选的模拟晶胞，则所选的模拟晶胞内的每个粒子的非静电对势可具有来自位于截止半径内的所选模拟晶胞内和外的任何和所有其他粒子的贡献。然后可以通过对所选择的模拟晶胞内的粒子的所有不同的非静电对势求和来获得模拟晶胞的总势能。包括多个模拟晶胞的超晶胞的总势能然后可以通过将这个和与模拟晶胞的总数相乘来获得。这提供了该系统的非静电构型能量，从而允许使用另外的方法(如考虑静电相互作用和外部
压力的影响)来确定构型能量。
19.当前描述的方法允许更准确地确定系统的构型能量，而不会预期到增加系统的坐标的数目。这降低了用于后续优化过程(诸如盆地跳跃技术)以找到系统的全局最小值的所需计算能力。
20.在示例中，所选的模拟晶胞内的粒子的总非静电对势还可以包括或具有来自位于所选的模拟晶胞外但是仍然在超晶胞内的粒子的截止半径内的粒子的贡献。
21.如上所述，可以理解，可以使用标准最小图像惯例来执行求和，以保持超晶胞内的粒子数量。这可以确保超晶胞内的粒子数目是守恒的——在模拟过程中粒子位置通常不是固定的。因此，可能存在以下情况：在优化方法期间一个或更多个粒子可能离开超晶胞，从而导致系统的势能跳跃。在这种情况下，当使用标准最小图像惯例执行上述求和时，超晶胞内的粒子数量是守恒的。
22.然后通过将每超晶胞单元的总非静电势能除以模拟晶胞的总数，可以获得每模拟晶胞的非静电势能(在常规方法中使用的晶体结构预测的传统最终结果)。
23.在实施例中，该方法可以还包括以下步骤：将构型能量除以模拟晶胞的总数以定义每模拟晶胞的非静电势能。
24.如本公开中所描述的构型能量可以考虑静电势能和非静电势能两者，并且可以任选地还包括来自非零外部压力的贡献。
25.根据本公开的第二方面，提供了一种用于确定具有多个粒子的系统的全局最小构型能量的计算机实现的方法，所述方法包括以下步骤：i)根据第一方面的任何部分，针对粒子的一种布置，计算系统的每模拟晶胞的非静电势能；ii)将构型能量除以模拟晶胞的总数以定义每模拟晶胞的非静电势能(如果尚未确定)；以及iii)使用盆地跳跃全局优化算法确定对应于粒子的一个或更多个晶体结构，而所述粒子对应于每模拟晶胞的焓的局部最小值，其中每个模拟晶胞的焓包括每模拟晶胞的非静电势能。
26.每模拟晶胞的焓可具有来自粒子间的静电相互作用；截止半径之外的长程相互作用；以及来自非零外部压力的贡献。因此，这个步骤可以还包括以下步骤：确定作用在系统上的外部压力并且将构型能量限定为每模拟晶胞的焓h(x)，其中x是定义模拟晶胞内的粒子的真实空间坐标的向量。此外，每模拟晶胞的焓可以包括来自粒子间的静电相互作用的贡献。另外地或可替代地，每模拟晶胞的焓可以包括来自截止半径之外的相互作用的贡献。
27.当考虑静电相互作用时，例如，当每个粒子包括一个或更多个多极时，第二方面的实施例可以包括以下步骤：通过确定粒子多极之间的收缩来确定粒子间的静电相互作用，然后使用埃瓦尔德和(ewald sum)与非静电相互作用以上文和下文所描述的方式合并。
28.在示例中，将多极相互作用从笛卡尔坐标系转换成球谐函数的步骤可以提供呈适合于实现成埃瓦尔德和的形式的多极相互作用。
29.可以认识到，转换步骤可以包括以下步骤：将多极相互作用图解地表示为一系列节点和从这些节点辐射的辐条，其中每个节点表示定义粒子的多极的对称多极张量，并且其中从每个节点辐射的辐条的数量等于那个节点的对称多极张量的秩。另外，该方法可以还包括将相互作用的粒子多极的辐条连结以在相应的节点之间形成辐条连接的步骤，每个辐条连接表示节点之间的相互作用。此外，作用在任何两个节点之间的收缩程度可等于在两个节点之间共享的辐条连接的数量。
30.此方法提供笛卡尔与球谐函数表示之间的直接连接，使得在两个表示之间变换变得直接，且最终表示使其自身易于在埃瓦尔德和型方法中实施。
31.图解表示的步骤还可以包括以下步骤：对于每个节点，编织所述辐条以将所述节点的每个辐条从笛卡尔分量变换成球谐函数形式。附加地或替代地，图解表示的步骤还可以包括以下步骤：在一块接一块的基础上编织节点之间的辐条连接，其中每块构成节点之间的辐条连接的子集。
32.在一个实施例中，对称多极张量可以是无迹的。这允许球谐函数被用作正交基以表示对称多极张量。
33.一旦确定系统的焓，则可以应用优化技术(诸如改进的盆地跳跃全局优化算法)以找到系统的焓的全局最小值。
34.盆地跳跃算法通常是通过在变换的势能表面上执行行走而工作的全局优化方法，其中变换的或
‘
平稳的’势能表面由每个点处的局部最小值的能量限定，该能量通过从该步上的坐标开始执行数值优化而获得。经变换的表面移除最小值之间的许多障碍，且已表明，在此表面上的行走具有对低的最小值(包含全局最小值)取样的更大机会。
35.因此，盆地跳跃全局优化算法可以包括以下步骤：a)通过采用局部优化算法获得具有坐标x的局部最小值h(x)；b)生成随机位移向量δx以获得新的试探坐标x
trail
＝x+δx；c)如果x
trail
产生大于或等于设置的最小距离r
min
的模拟晶胞内的任何两个粒子间的间距，则接受x
trail
，或者如果超晶胞内的任何两个粒子间的间距小于r
min
，则拒绝x
trail
；d)重复步骤b)到c)直到找到可接受的x
trail
的值；e)通过在h(x
trail
)上采用局部优化算法计算每模拟晶胞的变换焓h
min
(x
trail
)；f)如果满足标准的metropolis monte carlo标准：r《min[1,exp(-β(h
min
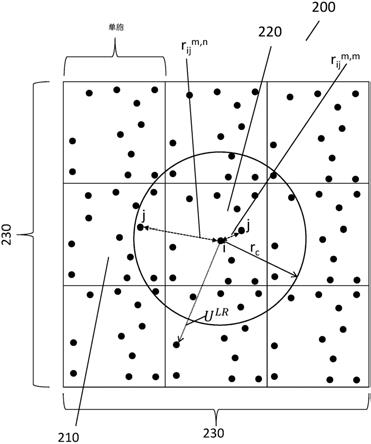
(x
trial
)-h(x)))]，则接受h
min
(x
trail
)并且设置x
trail
＝x，其中r是0和1之间的均匀随机数，并且其中kb是玻尔兹曼常数；否则，拒绝h
min
(x
trail
)并且将x返回到拒绝之前最后接受的局部最小值的值；以及g)重复步骤b)和f)以计算h(x)的多个局部最小值。然后，系统的全局最小值可以是来自h(x)的多个计算的局部最小值中最低的局部最小值的值。
[0036]
如上所述，在下一步骤中，可以生成随机位移向量δx以获得新的试探坐标x
trail
＝x+δx，其中x是系统中的粒子的初始坐标。然而，由于盆地跳跃方法通常使用相当大的蒙特卡罗步长，所以该试探步骤可能使分子非物理地靠近另一个分子移动，从而导致巨大的力。这可能导致以后局部优化算法的问题，使得难以找到局部最小值。为此，可以限制许多可能的试探移动，使得仅允许其中每个分子间粒子对大于指定的最小距离r
min
的构型。如果试探移动不满足这个标准，则可以生成新的试探移动，直到该算法找到满足标准的移动。因此，r
min
可受设定的最大值约束。
[0037]
在一些实施例中，粒子可以被认为是分子。因此，h(x)包括来自与模拟晶胞内的分子的构象异构体对应的分子内势能的贡献。此外，在步骤g)中，计算h(x)的多个局部最小值可以包括考虑来自构象异构体数据库的分子的不同构象异构体，其中每个构象异构体对应于该分子的分子内势能表面的局部最小值。另外，步骤g)还可包括计算h(x)的多个局部最小值，还可包括计算转变概率，所述转变概率指示分子在给定温度下从一种构象异构体转变到另一种构象异构体的概率。可以改变温度以确保系统最终将以合理的概率访问每个构象异构体。
[0038]
此实施例使用计算方法(例如密度泛函理论(dft))来生成可能的构象异构体结构
的初始集合，所述初始集合然后用来确定具有最低局部最小值的多个构象异构体。然后，可以放松得到的最佳结构(即，具有最低全局最小能量的那些结构)以产生新的构象异构体，这些新的构象异构体进而可以被反馈回构象异构体数据库中。另外地或可替代地，可以根据以上方法来识别与势能格局(potential energy landscape)的局部最小值相对应的构象异构体，以构建构象异构体的初始数据库。然后可以使用该构象异构体的初始集合来确定可能的晶体结构。然后可以使用dft放松最佳结构(即，具有最低能量的那些)以产生新的构象异构体，该新的构象异构体可以增加到构象异构体数据库以准备进一步的晶体结构预测。这可以被重复以改进构象异构体数据库的质量。
[0039]
根据更新的构象异构体数据库，可以确定给定构象异构体的可能的晶体结构及其相关的构型能量。这允许为这些构象异构体预测更多的晶体结构，直到确定了系统的
‘
真正’的全局最小值。总焓因此可以被认为包括对应于该分子的构象异构体的分子内能量。
[0040]
如果新的试探坐标被接受，那么可以应用标准的metropolis monte carlo标准来决定是接受还是拒绝具有新的试探坐标的变换焓。应用标准的metropolis monte carlo标准可以通过降低遇到大量连续拒绝的概率来提高盆地跳跃全局优化算法的效率。
[0041]
如果不满足标准的metropolis monte carlo标准，则可以在拒绝之前将x返回至最后接受的局部最小值。然而，如果满足该标准，则生成新的试探坐标并且重复该过程直到找到全局最小值。
[0042]
在一个实施例中，可以允许超晶胞的尺寸在盆地跳跃全局优化过程期间变化，使得超晶胞总是足够大以保持其截止半径。
[0043]
在一个实施例中，该系统包括药物候选物，并且其中每个晶体结构包括药物候选物的多晶型物。这允许为药物候选药品确定稳定的多晶型物，使得可以确定药物产品的稳定的对映异构体或多晶型物，减少临床试验所花的时间并且允许在很短的时间内(数周vs数月)，并且以更自动化的方式，对多晶型物形态进行比通过粉末x射线衍射必须发现的更彻底的搜索。进而，多晶型物和最热力学上稳定的多晶型物的这种知识可以用于告知/改进粉末——x射线衍射，并且允许测试以确保实际上制造了最稳定的多晶型物。
[0044]
此外，监管机构(例如，us fda)要求特定的(生物活性的)多晶型物在其热力学/动力学稳定性方面被恰当地表征。本实施例使得这比传统的晶体结构预测技术更简单。
[0045]
虽然对于药物产品候选物搜索和多晶型物确定存在益处，但所描述的方法可以用于其他工业中，如材料发现(或”材料基因组学”)，例如光伏、光电化学水分解、笼形晶体结构中的气体储存等。确保所生产的最终材料的热力学稳定性在这些工业中是重要的，以确保所生产的材料具有稳定的晶体结构。使用所描述的技术来确定最稳定的候选晶体结构，这对于结构材料(例如，量化强度等)也可能是重要的。
[0046]
根据本发明的第三方面，提供了一种确定系统的晶体结构的计算机实现的方法，如药物产品，所述系统具有多个粒子，并且所述方法包括以下步骤：确定药物产品的可能的晶体结构多晶型物，每个晶体结构包括重复的单胞；计算每个晶体结构的构型能量的全局最小值；将所述构型能量除以所述模拟晶胞的总数，以定义每模拟晶胞的非静电势能；以及使用盆地跳跃全局优化算法来确定每模拟晶胞的构型能量的全局最小值，其中计算全局最小值的步骤包括以下步骤：i)定义截止半径，所述半径定义该系统中的粒子间的非静电相互作用电势截止距离；ii)定义一组晶胞向量以生成模拟晶胞；iii)定义一组超晶胞向量以
生成超晶胞，其中所述超晶胞包括该模拟晶胞的多个副本；iv)对于位于该超晶胞内的每个粒子，计算该粒子与该截止半径内围绕该粒子的任何和所有另外的粒子的最近图像之间的非静电对势，所述非静电对势由该粒子与位于该截止半径内的任何和所有其他粒子的相互作用产生；以及v)将所有不同的非静电对势求和以提供该系统的非静电构型能量；vi)将该构型能量除以模拟晶胞的总数以定义每模拟晶胞的非静电势能；以及vii)使用盆地跳跃全局优化算法来获得构型能量的多个局部最小值，并且通过选择最低的局部最小值为全局最小值，确定每模拟晶胞的构型能量的全局最小值，并且其中单胞等同于模拟晶胞；并且选择具有最低全局最小值的晶体结构多晶型物作为该药物产品的候选。
[0047]
给定确定的晶体结构，则可以确定这种结构的潜在性质，并因此确定对于给定的化学组成如何控制促进这种晶体结构的必要参数。鉴于晶体结构可能对患者对药物化合物的生理反应具有如此重要的影响，使用上述方法确定晶体结构在集中试验和研究工作中提供了明显的益处。
[0048]
上述方法提供了用于确定晶体结构的可靠技术，而不需要进行潜在的有害或危险的晶体结构试验。
[0049]
可以理解，对于第一、第二和第三方面，截止半径可以等于或大于晶体结构的单胞。
[0050]
根据本发明的第四方面，提供了一种用于执行根据前述方面的任何实施例的方法的计算机程序。
[0051]
因而，可提供一种计算机程序，当在计算机上运行所述计算机程序时，所述计算机程序使所述计算机配置任何设备，包括电路、控制器、传感器、滤波器或本文中所公开的设备，或执行本文中所公开的任何方法。作为非限制性示例，计算机程序可为软件实施，且计算机可视为任何适当的硬件，包括数字信号处理器、微控制器和只读存储器(rom)、可擦除可编程只读存储器(eprom)或电子可擦除可编程只读存储器(eeprom)中的实施。软件实施可以是汇编程序。
[0052]
根据本发明的第五方面，提供了一种保存根据第四方面的计算机程序的数据介质。
[0053]
例如，计算机程序可以被提供在计算机可读介质上，计算机可读介质可以是物理计算机可读介质，诸如盘或存储器设备，或者可以体现为瞬态信号。这种瞬态信号可以是网络下载，包括互联网下载。
[0054]
根据本发明的第六方面，提供了一种计算机系统，其上加载有根据第四方面的计算机程序。
[0055]
本公开的方面允许确定复杂固态系统的晶体结构，例如药物化合物、工业结晶材料等，如金属、半导体、聚合物、蛋白质配体复合物中的药物等。
[0056]
可以理解，确定可能的晶体结构的步骤可以包括根据分析或其化学组成的估计来确定晶体的可能的构型的步骤。此外或备选地，可以利用从标准晶体结构生成的和基于标准晶体结构的相关构型来进行迭代方法。
[0057]
现在将参考附图描述本发明的优选实施例，其中：
附图说明
[0058]
图1是用于计算包括多个粒子的系统的构型能量的已知方法的示意图；
[0059]
图2是根据本发明的用于计算包括多个粒子的系统的构型能量的方法的示意图；
[0060]
图3a至图3l示出了由使用图2的方法计算的构型能量确定的水冰的示例晶体结构。
[0061]
应注意的是，这些图是示意性的并且不是按比例绘制的。在附图中为了清楚和方便起见，这些图的部分的相对尺寸和比例已经在尺寸上被放大或者缩小地示出。相同的参考标记通常用于指代经修改和不同实施例中的对应或相似特征。
具体实施方式
[0062]
图1示出了使用常规方法确定构型能量的已知示意性技术。在该方法100中，根据单胞向量130定义单胞110(在该图中在2d中示出-还将存在第三维)。每个单胞110限定边界，构成晶体结构的单胞的粒子112被约束在边界内，并且每个晶胞110是晶体的重复单元结构。
[0063]
为了确定系统100的构型能量，使用单胞110内的每个粒子112来计算所选择的粒子112与位于由截止半径rc限定的边界120内的所有其他粒子112之间的势能u。这包括位于单胞110的边界之外的粒子。
[0064]
作为示例，对于粒子，计算对势(即，位于彼此的截止半径内的两个粒子间的势能)。因此，对于与次级粒子j相距r
ij
的粒子i，计算对势。考虑到长程势能u
lr
和来自外部压力的贡献，这些对势的总和允许计算构型能量。然后可在计算出的构型能量上使用盆地跳跃或其他全局优化技术，以收敛到对应于稳定晶体结构的全局最小值。
[0065]
图2中示出了本发明中使用的方法或技术。在该示例中，系统200包括布置在标称晶体结构中的多个粒子212，例如，在有系统地遇到更多最小值之前，该晶体结构基于系统的化学成分或通过在盆地跳跃过程中遇到的第一局部最小值来估计。在该示例中，基于具有重复的晶体结构的估计晶体结构来选择晶胞或模拟晶胞210。
[0066]
然后可以基于模拟晶胞限定超晶胞向量230，使得整数个模拟晶胞或单胞210适合每个超晶胞向量230。超晶胞向量230(包括未示出的第三向量)一起限定晶体结构的超晶胞。该超晶胞包括系统的整数个晶胞或模拟晶胞210，因此包括多个重复的晶体结构。
[0067]
然后可以采用与图1类似的技术。然而，可以理解，由截止半径rc限定的边界220大于图1所示的已知技术中的边界。特别地，较大的截止半径包括位于单胞110的边界外面的粒子。实际上，现在考虑处于相同位置但位于相邻晶胞或模拟晶胞210中的粒子的相互作用。
[0068]
作为示例，对于粒子，计算对势(即，位于彼此的截止半径内的两个粒子间的势能)。因此，对于与次级粒子j1相距r
ijm,m
的粒子i，计算对势。然而，在不同的单胞中位于与粒子j1相同的构型位置的次级粒子j2也可以具有由于它与粒子i的距离r
ijm,n
而确定的对势。
[0069]
考虑到长程势能u
lr
和来自外部压力的贡献，这些对势的总和允许计算构型能量。然后可在计算出的构型能量上使用盆地跳跃或其他全局优化技术，以收敛到对应于稳定晶体结构的全局最小值。
[0070]
更具体地，对于具有周期性边界条件的系统，其中每单胞n个粒子在非静电对势下
相互作用，其中具有间距r的一对粒子的能量由u(r)给出，当r
→
∞时u(r)
→
0；每模拟晶胞的构型能量u通常被认为近似为：
[0071][0072][0073]
其中其中是所谓的r
ji
＝r
j-ri的最小图像，其中i和j是一个模拟晶胞内的第i和第j个粒子。u
lr
(rc)是对能量的长程校正，其近似截止范围之外的相互作用。通过均匀分布u(r)逼近在r》rc处的粒子的密度，此长程校正采取以下形式：
[0074][0075]
其中v＝a.(b
×
c)是晶胞体积，并且是单胞的倒易晶胞向量(reciprocal cell vectors)。
[0076]
等式1右侧的总和的条件j》i是为了防止相同的对势被包括多于一次。因此，等式1仅对模拟晶胞内的不同对势求和。另外，等式1中的和仅针对的对势，其中rc是截止半径。
[0077]
此外，该系统的每模拟晶胞的总构型能量还包括粒子之间的静电相互作用。下面解释如何估计这一点的细节。
[0078]
还要注意，在非零压力的情况下，以上要由pv项补充，以给出每模拟晶胞的焓：h＝u+pv，其中p是外部施加的压力并且v是晶胞体积。
[0079]
当在模拟期间一个或更多个粒子离开模拟晶胞时，需要最小能量过程来防止势能的跳跃。最小图像和截止半径rc协同工作以限制能量和，以仅包括周期性系统中的位于截止范围内的那些在平移上不同的对相互作用。在标准方法中，限制截止半径的尺寸，使得相关联的截止范围适合在单胞内部。这需要与最小图像过程一致，该最小图像过程总是返回一个单胞内的向量。
[0080]
然后，截止半径rc的最大值由可以适合在三斜晶胞内的最大范围确定，并且不难证明，对于晶格向量130a、b、c的单胞110，这样范围的半径必须满足下列条件：
[0081][0082]
其中a
*
＝|a
*
|是倒易晶胞向量的大小，并且对于b
*
和c
*
也是类似的。
[0083]
为了足够快的收敛相互作用，能量和(包括长程校正)通常非常接近每单胞的实际能量，即当整个周期性系统被考虑在内时，并且在极限的情况下，它应该收敛到理想结果。然而，虽然能量和成立，截止半径也总是受到模拟晶胞的尺寸的限制。
[0084]
由此，获得收敛的结果要求模拟晶胞210足够大以包含足够大的截止范围。
[0085]
为了克服这个问题，本发明使用具有晶胞向量230maa,mbb,mcc的超晶胞，其中a、b、c是原始模拟晶胞的晶胞向量130。ma,mb,mc是整数，并且在超晶胞包括m＝mambmc个副本的情况下，每个副本与原始模拟晶胞相同。
[0086]
在第m个副本或晶胞/模拟晶胞210中的第i个粒子的坐标由下式给出：
其中rm＝maa+mbb+mcc是由单胞向量110的整数倍生成的晶格(lattice)。
[0087]
而且，如果r
ji
＝r
j-ri是模拟晶胞中的两个粒子之间的对向量，则是跨副本的粒子之间的对向量的向量。
[0088]
标准最小图像过程可以应用于超晶胞。将定义为r的超晶胞最小图像，的超晶胞最小图像由以下给出：
[0089][0090]
其中
[0091][0092]
是超晶胞晶胞向量的矩阵(在此以上三角形式呈现)。
[0093]
截止半径rc现在必须适合在超晶胞内部，并且因此必须满足以下条件(c.f.等式3)：
[0094][0095]
假设在模拟过程期间允许模拟晶胞向量120改变。通常，截止半径rc在模拟过程期间保持固定，但是超晶胞的尺寸不固定，并且控制其尺寸的ma,mb,mc整数可以动态调整，使得超晶胞总是足够大以保持其截止范围。这些值可以通过对等式6求逆来计算，以获得：
[0096]
ma＝int(2r
ca*
)+1,
ꢀꢀꢀꢀꢀ
(7)
[0097]
并且对于mb和mc也类似，其中int(x)函数(针对正自变量)向下舍入到最近的整数。
[0098]
每副本(即，每模拟晶胞)的能量通过在小于截止半径的超晶胞中的每个对相互作用上求和并且除以副本数量m而给出。除了长程校正，该能量由下式给出：
[0099][0100]
其中m和m
′
的和是针对超晶胞中的所有m个副本，并且其中假设该和不包括描述每个粒子与其自身的相互作用的非物理项。通常，仅计算截止半径内的相互作用。
[0101]
原则上，以上方法应该起作用，但是它是非常浪费的，因为它涉及多次对平移上等效的对相互作用进行计算。事实上，可以看出等式8对每个不同的ij相互作用求和m次，对于超晶胞中的每个副本一次。
[0102]
为了移除过度计算，首先考虑以下恒等式：
[0103][0104]
其之所以成立，是因为lhs对超晶胞中与rj的每个副本的相互作用求和，并且
rhs对超晶胞中与rj的每个副本的相互作用求和。然而，在周期性边界条件下，和描述相同的粒子，仅在不同的副本中，因此这两个和必须相等。
[0105]
使用上述结果，可以得出：
[0106][0107]
当应用于等式8时，其给出能量和作为副本的单个和：
[0108][0109]
因为ij和ji都被求和，所以仍然存在过度计算问题。对于等式1，这可以通过将和限制为j》i来避免。这对于i≠j相互作用工作良好，但是i＝j相互作用不能这样被求和。单独考虑这些相互作用，并且使用恒等式则能量和的超晶胞版本的最终形式是：
[0110][0111]
从等式12可以看出，截止半径不再被限制为适合在模拟晶胞内，而是现在可以使其任意地大。并且照常，有可能用等式2的长程校正来补充以上内容，以便将截止范围之外的相互作用考虑在内。
[0112]
图2示出了在实际空间中的上述超晶胞方法。该过程非常类似于等式1的标准能量和，除了它涉及副本的和；现在相对于超晶胞晶胞向量应用最小图像；并且现在还必须对粒子与其副本的相互作用求和。
[0113]
现在已经发现了用于处理小单胞的方法，可以使用盆地跳跃方法的变体来找到系统的全局最小值。
[0114]
在盆地跳跃方法中，模拟在经变换的势能表面u
′
上进行，其由下式给出：
[0115]u′
(x)＝u
min
(x)
ꢀꢀꢀꢀꢀ
(13)
[0116]
其中x＝x1,x2,...xn是指定系统的n个坐标，并且u
min
(x)是在势能表面u下从x开始的局部最小值。即，u
′
(x)通过使用局部优化算法获得，该局部优化算法从初始坐标x开始，然后下坡行进直到它找到局部最小值。还要注意，在外部施加压力的情况下，将使用经变换的焓表面h
′
(x)＝h
min
(x)。
[0117]
在该方法中，通常使用metropolis monte carlo(米特罗波利斯蒙特卡罗)算法来在经变换的势能表面中走动。这将导致系统访问一系列不同的局部最小值，希望如果模拟运行得足够长，则其可能最终找到其到全局最小值的路径。
[0118]
大多数局部优化算法需要能量和能量关于每个坐标的导数，即它们需要被提供有针对x的任何值返回n个导数的子例程。为了使其在计算上更有效，通常需要分析地实现这些导数。
[0119]
在当前情况下，一组方便的坐标由以下给出：i)对于i＝1..n
mol
，3n
mol
个分子质心位移其中n
mol
是每单胞的分子数目(其中3表示x、y和z)；ii)3n
mol
个欧
拉角φi,θi,ψi，指定每个分子围绕其质心的旋转；以及iii)6个独立的晶格参数，a
x
,b
x
,by,c
x
,cy,cz。因此，该代码需要被提供有分析导数以及(类似组成)。
[0120]
在经变换的表面上使用monte carlo(蒙特卡罗)算法时遇到的问题是通常将存在大量的连续拒绝；其中蒙特卡罗有效地陷入了由多个更高的最小值包围的区域中。
[0121]
为了克服这个问题，使用改进的盆地跳跃算法(盆地逃脱算法)，其中行走以局部最小值开始并且采取步骤直到它遇到拒绝，在这种情况下，行走重置到其局部最小值的位置，x
→
x
min
(x)，从该处开始其在行走的下一次迭代上进行下一步。通常情况是这个局部最小值与它从其开始的那个相同，但是不需要如此，因为在一些情况下，行走将已经成功地从一个最小值的盆地逃脱到另一个最小值的盆地。在后一种情况下，拒绝将导致行走被重置到新最小值的坐标。
[0122]
发现这种简单的零参数的改进实质上提高了算法的效率，因为它实质上解决了行走陷入高拒绝区域中的问题。
[0123]
盆地跳跃方法典型地使用相当大的蒙特卡罗步长，并且遇到的另一个问题是偶尔试探步骤可能使分子非物理地靠近另一个分子移动，从而导致非常大的力。这能引起局部优化算法的问题，使得难以找到局部最小值。
[0124]
为了解决这个问题，限制允许进行蒙特卡罗行走的可能试探移动的数量，这样使得有效的试探移动是其中每个分子间粒子对大于指定的最小距离的构型。如果试探移动不满足这个标准，则生成新的试探移动直到算法找到满足这个标准的移动。
[0125]
从例如高斯分布中选择产生新的试探坐标所需的δxi随机位移。然而，可以理解，也可以使用其他均匀分布。更明确地，每一分数坐标中的位移取自具有西格玛值σf和随机变量xf的高斯分布，欧拉角的位移取自具有西格玛值σe的高斯分布，并且六个晶胞向量分量中的每个晶胞向量分量中的位移取自具有西格玛值σc的高斯分布。σf,σe,σc的值是可调节的参数，其影响盆地跳跃的效率。逆温度(其中kb是玻尔兹曼常数，并且t是温度)也是一个可调参数，并且通常应被选择为使得系统具有有时会接受向更高能量/焓的移动的合理概率，这样使得系统可以克服障碍。然而，温度不应该太大，以致行走基本上用了其全部时间来探索高能量构型。
[0126]
点电荷静电模型典型地通常用于计算粒子的静电势能，其中通常进行埃瓦尔德求和(ewald summation)以确保能量和的快速收敛。近年来，已经开发了几种方法来在电荷分布的多重展开中包括高阶的项(其中在接下来的三个等级中的项由四极、八极和十六极等的名称指代)。然后挑战是识别如何修改埃瓦尔德求和或类似的算法，这样使得它可以正确地处理高阶多极相互作用。
[0127]
以下详述球谐函数中的多极相互作用的示例推导，其不要求球谐函数理论的任何详细技术知识。
[0128]
基本上，该方法包括根据笛卡尔推导多极相互作用。然后将该相互作用转换成球谐函数形式。这是借助于三个关键想法来完成的：i)使用多极位点之间的相互作用的图解表示，其极大地阐明了数学——因为其证明完整的相互作用可以在“图之和”型意义上计算；ii)使用球谐函数来为无迹多极张量构造正交基，使得可以通过斯顿的球谐函数表格来实现笛卡尔到球谐函数的转换；iii)在被称为编织的过程中，在一块接一块的基础上将笛
卡尔变换成球谐函数，其中每块构成全部数量的该多极的笛卡尔分量的子集；变换如何通过采取线性组合来交织笛卡尔的图解象征。下面是该方法的概述。
[0129]
考虑在位置r+δrm处具有电荷qm的一簇nc电荷，其中δ用于表示位移通常非常小(至少，它们比从分布中探测场的任何测试部位更接近r)。然后我们根据下式定义分布相对于r的秩n笛卡尔多极张量m
(n)
：
[0130][0131]
其中δr
m(n)
＝δrmδrmδrm..是张量乘积，其中笛卡尔分量..是张量乘积，其中笛卡尔分量其中每个希腊索引是x、y、z之一，并且在乘积中存在n个类型因子
[0132]
注意，在等式14中并且对于本说明书的其余部分，逆阶乘被包含在每个多极的定义中，但是其他方法可以使用不同的惯例。
[0133]
作为标量的秩0多极m
(0)
，仅是电荷之和。秩1多极m
(1)
多极被称为偶极矩，并且是具有分量的向量。秩2多极m
(2)
被称为四极，并且具有9个分量：等，并且具有27个分量的秩3多极被称为十六极，等等。
[0134]
从其在等式14中的定义中清楚的是，每个多极张量在其索引的任何排列下是对称的。例如，对于秩3的多极张量，m
αβγ
＝m
αγβ
＝m
βγα
＝m
βαγ
＝m
γαβ
＝m
γβα
。此外，可以表明在任何轴坐标系中都是如此。这种排列对称性意味着多极张量属于被称为对称张量的类别。
[0135]
这些多极是有用的，因为该簇的静电特性通常可以按照在递增秩的多极矩上的快速收敛级数来书写，而不是必须对单独的电荷本身求和。为了看到这一点，将电荷分布置于背景不均匀静电势φ(r)中。然后，由下式给出由于φ(r)引起的簇的静电能量u(r)：
[0136][0137]
现在，使用内积符号《a
(n)
,b
(n)
》，其中《a
(n)
,b
(n)
》指示张量a
(n)
和b
(n)
的内积，可以示出：
[0138][0139]
φ(r+δrm)的泰勒级数展开可以被写为：
[0140][0141]
其中具有分量
……
[0142]
上述更简明的撰写方式为：
[0143][0144]
其中φ
(n)
(r)是根据下式从φ(r)的重复定向导数创建的秩n场张量：
[0145][0146]
类似地，从多极的基本理论，并且从使用另一个泰勒级数展开可以示出，来自原点周围的电荷簇的r处的静电势(具有多极m
(n)
)由以下给出：
[0147][0148]
其中4π∈0＝1以简化公式。
[0149]
因此，假设以上强烈收敛，为了从电荷簇计算静电势，合理的是忽略电荷分布的精细细节并且仅用其多达最大秩的多极工作，其中这些多极是从等式14中电荷分布的多极展开来计算的，并且其中这些多极被放置在多极展开位点上，在这种情况下是在原点处。
[0150]
现在考虑多极矩的痕迹。在秩2的情况下，只有一条痕迹，其由给出，并且将证明对于由下式定义无迹秩2张量是有用的：
[0151][0152]
其中tr[m
0(2)
]＝0(设计地)
[0153]
就无迹和痕量组分而言，背景静电势中的秩2多极张量的能量通过以下给出：
[0154][0155]
上式中的最后一项涉及静电势的拉普拉斯算子。然而，根据基本静电学，可以示出拉普拉斯算子在自由空间中消失，并且因此最后一项为零。因此，四极的痕迹对总能量没有贡献，并且无迹四极总是可以代替它使用。类似地，可以去除更高秩多极的痕迹，因为它们对能量没有贡献。
[0156]
可能争论的是，在实际系统中，拉普拉斯算子不为零，因为任何实际原子位点将经历来自其他粒子的原子间和分子间电荷云的非零电荷密度。然而，用于原子间静电能的标准多极展开没有考虑到此类影响，并且此后它们将被假定为零。
[0157]
用无迹形式的r张量工作通常也更方便。根据已知的定理，r张量的无迹形式可以从1/r的重复梯度经由下式来定义：
[0158][0159]
其中s
(n)
是用于无迹r
(n)
张量的符号，并且其中前几个项由下式给出：s0＝1,并且其中s
(n)
的无迹性来自1/r的消失拉普拉斯算子。
[0160]
考虑到这些梯度由james clerk maxwell研究，并且考虑到尽管它们不是正交的，但它们在许多意义上表现得像球谐函数多项式的笛卡尔模拟(稍后将详细介绍)，因此可以将s
(n)
称为麦克斯韦笛卡尔球谐函数。
[0161]
将以上等式23代入等式20中给出：
[0162]
[0163]
其中以上最后一项来自认识到由于m
(n)
是无迹的，那么r
(n)
的痕迹对《m
(n)
,r
(n)
》内积没有贡献(使用用于内积中的多极痕迹的消失贡献的相同自变量)。因此，鉴于s
(n)
是r
(n)
的无迹形式，我们具有《m
(n)
,r
(n)
》和《m
(n)
,s
(n)
》是相同的。
[0164]
这些梯度在多极的理论中起中心作用，如从最后部分应该已经明显的。然而，多极相互作用的埃瓦尔德和模拟要求计算更一般的梯度，其中球对称函数(在此写作b(r))代替像等式20的表达式中的1/r项。即，代替计算梯度，现在更希望的是找到梯度且知道如果需要非ewald正则多极展开的结果，则可以简单地在最终表达式中设置。
[0165]
具体地，与普通多极公式类似的埃瓦尔德和要求使用内核，其中erfc(x)是互补误差函数，其对应于单位电荷与负高斯
‘
屏蔽’密度的相互作用，其中屏蔽密度是形式ρ(r)＝-aexp(-a2r2)(适当地归一化)。
[0166]
为了简化这些梯度计算径向函数，可以定义bm(r)，其中第零项由b0(r)＝b(r)给出，并且高阶项根据下式来定义：
[0167]bm+1
(r)＝-b
′m(r)/r
ꢀꢀꢀꢀꢀ
(25)
[0168]
从其得出，如果
……
，则
……
，并且，通常，其中！！是双阶乘。
[0169]
如可预期的，当使用内核时，表达式稍微更复杂，但已示出了如何可经由简单的递归过程生成用于此情形的高阶函数。
[0170]
计算b0(r)函数的方向梯度中的前几项是有益的。先回顾一下，针对一般的球对称函数f(r)，可以证明。然后接下来是：
[0171][0172]
从其前两个方向导数评估为：
[0173][0174]
以及
[0175][0176]
其中括号中的项是具体选择的结果，并且其中这些项可以写在等式23中遇到的麦克斯韦笛卡尔球谐函数的项中。
[0177]
当然可以以此方式继续计算高阶项，但是在此要说明的要点是，对于l的某个值，以上b0(r)的前两个方向导数包含b
l
(r)中的项，并且通常，通过归纳，可以示出每个阶中的梯度项可以表示为b
l
(r)中的级数。
[0178]
返回到多极问题，假设在位置ri和rj处分别存在两个多极位点i和j，每个位点携带不同秩的一组多极，其中这些多极被放置在这些位点位置处。然后，该对的静电能是由于位点i上的每个多极与位点j上的每个多极相互作用，其可以通过首先根据等式20由ri处的多极评估rj处的场，然后根据等式18计算在该场的存在下在j上的多极的能量来确定。标记此能量u
ji
(r
ji
)，其给出：
[0179][0180]
其中r
ji
＝r
j-ri是位点间向量，r
ji
＝|r
ji
|，是相对于rj的梯度，并且其中使用包含b0(r
ji
)内核的更通用形式。
[0181]
类似于如何示出b0(r)的重复梯度中的每个阶项都包含b
l
(r)中的级数，不难看出对于相互作用能量u
ji
(r
ji
)必须也是如此，并且，这可以通过收集b
l
(r
ji
)中的项来写成下式来明确：
[0182][0183]
其中函数可以被认为是b
l
(r
ji
)中的系数。
[0184]
评估这些函数似乎需要
‘
用手’对项进行计算和求和，就像其将涉及非常乏味的代数。然而，封闭形式的解决方案是已知的，并且由下式给出：
[0185][0186]
其中r
(n)
＝rrr
…
；多极都被假定为无迹的；符号a.d.b表示a和b的张量指数的d倍收缩；di是包含mi的括号中的收缩的数量；dj是包含mj的括号中的收缩的数量；dc是在这两个括号之间作用于中心的收缩的数量，这些收缩被表示为内积；并且其中是由下式给出的整数组合系数：
[0187][0188]
等式31中的和覆盖所有的di,dj,dc，其中di+dc+dj＝l；di,dc,dj≥0,即，该和是针对具有l收缩的所有可能的项。
[0189]
等式31将被称为
‘
多极相互作用生成公式’，因为它生成静电能的多极-多极展开中的所有项。
[0190]
有可能构建等式31的多极相互作用生成公式的图解表示，其中图4中示出了一个这样的图。它示出了针对l＝6的多极相互作用生成公式中的一个项，对应于其中从左到右的节点表示r
ji(3)
(圆333)、m
i(5)
(圆328)、m
j(3)
(圆330)和r
ji(1)
(圆327)。规则是每个节点表示不同的张量，其中它的秩由从所讨论的节点辐射的辐条332的数量给出；在两个节点之间共用的辐条332的数量(即，连接的辐条的数量)等于在相应张量之间作用的收缩程度；并且当存在奇数个将j多极与其r张量连接的键时，该图的符号取奇数。
[0191]
还要注意，没有张量或节点326、328、330、327可键合到自身。鉴于自键对应于取张量的部分痕迹，这个规则直接来自于以下事实：m和r张量的痕迹对多极相互作用生成公式没有贡献。
[0192]
通常，当将多极相互作用实施到分子模拟代码中时，除了需要总能量之外，还需要
力、多极场、角导数和扭矩。
[0193]
让f
ji
(r
ji
)＝-f
ij
(r
ji
)是由于多极位点j与多极位点i的相互作用而在多极位点j上的力，其中j上的总力由给出。
[0194]
通过取等式30的梯度而求出该力，并评估为：
[0195][0196]
其中等式27用于求出b
l
(r
ji
)函数的梯度，并且其中从取等式32的梯度中求出这些函数，并且由下式给出：
[0197][0198]
在图5a和5b中示出了一个力项的图形表示，它们对应于从图4获取相互作用的梯度，并且等于
[0199]
比较图4和5a、5b，可以看出获取梯度导致连接i或j多极与其r张量的键之一断裂。这使该多极具有裸(或未键合)的辐条，当作为一个整体时其给出了秩1向量的图形表示。
[0200]
虽然已经提供了系统的总能量的表达式，但根据多极场张量，能量的一个可论证地更简洁的表达式可以写为：
[0201][0202]
其中φ
i(n)
是位点i上的秩n场张量，其由下式定义：
[0203][0204]
根据多极场书写的等式35具有明显的优点，即它允许将总能量自动分解成来自不同多极秩的贡献，即电荷、偶极、四极等。计算这些场的另一个原因是它大大简化了角导数和扭矩的计算，这些角导数和扭矩将在下一部分中给出。
[0205]
这些场可以通过求能量相对于每个多极的导数来计算。仅观察一对多极位点，由于位点i上的多极引起的多极位点j上的场由以下给出
[0206][0207]
其中取等式31关于多极的导数，我们获得
[0208][0209]
其中symm指示得到的张量元素将在所有索引排列上对称，并且它们的痕迹被移除。
[0210]
该最后一步是确保场张量与其相应的多极具有相同的对称性所必需的，因为根据它们的定义，场张量必须相对于它们的索引的任何排列不变。并且去除痕迹是因为场痕迹对能量没有贡献，因此这些场痕迹被设置为零是有意义的。
[0211]
在图6中示出了场计算的图形表示，其中示出了与图4或图5中的多极相互作用相对应的张量m
i(5)
(328)上的秩5场(334)和张量m
j(3)
(331)上的秩3场。从场张量节点(334，338)辐射的辐条332代表由它们的辐条332的数量给出的秩的多极场张量。具有中心节点334的星形340表示第i个位点上的秩5场张量，具有中心节点338的星形342表示第j个位点上的秩3场张量。这两个图都可以被认为是从图4中切出一个多极，这对应于取关于该多极的导数。因此，场张量334、338可以被认为是等同于在该图的右手侧示出的多极相互作用。换言之，场张量334等同于与m
ji(3)
(331).r
ji(1)
(327)相互作用的r
ji(3)
(333)张量的组合。类似的方法可应用于场张量338，包括组合的节点333，328：327。
[0212]
为了计算能量的角导数，让a
αβ
是将向量分量从参考系变换到试验室系的旋扭矩阵。此外，假设a
αβ
＝a
αβ
(φ,θ,ψ)，其中(φ,θ,ψ)是(三个)欧拉角并且我们希望求出关于这些角的能量导数。以欧拉角ψ为例，使用链规则从秩n多极获得贡献如下：
[0213][0214]
其中()n指示来自第n秩多极的贡献并且：
[0215][0216]
其中使用索引排列对称。通过对来自所有秩的贡献求和来获得总角导数。
[0217]
扭矩同样最好根据场来计算出来。扭矩向量具有多个分量，其中θ
α
是围绕α轴线的旋转角度，并且通过与以上类似的自变量，扭矩向量被计算为：
[0218][0219]
其中∈
αβγ
是levi-civita符号，并且其中在图7中给出了扭矩的图解表示。在该图中，用互连多极346和场348的两个辐条332a、332b来表示秩3多极或节点346与其秩3场348之间的相互作用。交叉乘积350也经由辐条332c、332d连接。得到的交叉乘积是具有另一个辐条332e(它的其他辐条332c、332d分别与多极和场互连)的秩3张量。
[0220]
这部分探讨了齐次多项式和对称张量之间的深层联系。
[0221]
假设是对称笛卡尔张量分量，其中αβγ..索引包含x的n
x
次出现、y的ny次出现和nz。定义n＝(n
x
,ny,nz)，其对于引入压缩张量符号将是有用的，其中：
[0222][0223]
其中总计，存在属于特定n的αβγ..索引的排列的多项式。
[0224]
现在假设p
(n)
(r)是n次的齐次多项式，从而使得p
(n)
(λr)＝λnp
(n)
(r)，其中λ是标量。例如，由p
a(3)
(r)＝4x3+2y2x-5y3给出3次齐次多项式。
[0225]
使用压缩符号，可以示出并且这可以将中的多项式系数标记为该条用来表示是多项式系数，否则其将被误认为是对称张量的分量。然后，通用n次齐次多项式可以写为：
[0226][0227]
其中和是针对n
x
+ny+nz＝n的n＝(n
x
,ny,nz)的所有值，并且已经引入了对称张量p
(n)
，该对称张量具有以下分量：
[0228][0229]
其中由于αβγ..索引的排列对称性，需要逆多项式系数。
[0230]
还可以形成内积《p
(n)
,a
(n)
》，可以将其计算为：
[0231][0232]
假设p
(n)
对多项式系数中的所有信息进行编码，p
(n)
可以被认为是的对称张量形式。
[0233]
还可以根据下式，通过梯度算子从多项式本身获得p
(n)
张量：
[0234][0235]
这可以通过将以上梯度算子应用于等式42来看到。使用等式44，等式45的逆由下式给出：
[0236]
p
(n)
(r)＝《p
(n)
,r
(n)
》
ꢀꢀꢀꢀꢀ
(46)
[0237]
等式45中的线性算子提供从齐次多项式到其对应的对称张量的映射。并且在等式46中存在逆的情况下，该映射是一对一的，从而在n次的齐次多项式与秩n的对称张量的向量空间之间创建同构。即，这两个向量空间：(i)由秩为n的对称张量描述的向量空间，以及(ii)由n次的齐次多项式描述的向量空间是等效的。
[0238]
现在可以引入所谓的调和多项式h
(n)
(r)，这些调和多项式是p
(n)
(r)多项式的子集，其具有消失的拉普拉斯算子，δ{h
(n)
(r)}＝0，其中是拉普拉斯算子算符。作为示例，一个这样的多项式由h
a(3)
＝2x3z+3x2y-6xy2z-y3给出，对其可以确认δh
a(3)
＝0。
[0239]
由于h
(n)
(r)上的消失的拉普拉斯算子条件，调和多项式是特别令人感兴趣的，因为它们对应的对称张量是无迹的。因此，线性算符在n次的调和多项式的向量空间与秩n的对称的无迹张量的向量空间之间创建同构。
[0240]
调和多项式，或等效地秩n无迹张量，被2n+1个线性无关向量跨越。为了看到这一点，首先考虑秩n的对称笛卡尔张量，对其很容易证明存在n＝(n
x
,ny,nz)的可能值，其中n
x
+ny+nz＝n。此外，不难证明对于对称的无迹张量，无迹条件强加约束，其留下了n
st
＝n
s-n
t
＝2n+1个独立分量。
[0241]
例如，可以描述仅具有n
st
＝5个分量的整个秩2张量m
(2)
。一种方法是挑选元素
从其我们通过使用无迹条件可以推断的值，并且我们可以从排列对称的使用中获得并且对于其余分量也是如此。
[0242]
给定上述情况，并且给定n次调和多项式与秩nit的无迹张量之间存在同构的事实，可以推断调和多项式对于n次也必须具有2n+1个线性无关分量。
[0243]
作为无迹对称张量的基的球谐函数。
[0244]
在最后一部分的结尾的讨论涉及以下事实：对称的无迹张量原则上可以由最小集合的2n+1个线性独立向量来描述。在仅使用此数量的分量的表示中工作显然是有利的，并且在本部分中将示出如何使用球谐函数来完成这一点，球谐函数为无迹张量提供自然的正交基。
[0245]
根据球谐函数的理论，内积可以根据下式从单位球面上的调和多项式的乘积的积分来定义：
[0246]
《h
a(n)
,h
b(n)
)》s＝∫h
a(n)
(φ,θ)h
b(n)
(φ,θ)ds
ꢀꢀꢀꢀꢀ
(47)
[0247]
其中下标s符号《，》s是指示这是球面内积，不与张量内积混淆。
[0248]
同样根据球谐函数的理论，《，》s内积的完整正交基由球谐函数(技术上，正则立体调和)提供，球谐函数包括在单位球面上正交的一组2n+1个实调和多项式，从而使得将球谐多项式写为q
i(n)
(r)，并且假设适当的归一化，给出：
[0249]
《q
i(n)
,q
j(n)
》s＝δ
ij
ꢀꢀꢀꢀꢀ
(48)
[0250]
其中i,j在[0,2n+1]范围内。
[0251]
应注意，球谐函数可用于描述限于单位球面的任何调和多项式。然而，在当前情况下，项球谐多项式具体地是指在单位球面上正交的一组q
i(n)
(r)个多项式。
[0252]
通过应用等式45，球谐函数的无迹张量形式q
i(n)
还可以被定义为：
[0253][0254]
使用等式46，其具有由下式给出的逆：
[0255][0256]
现在，假定(i)调和多项式和(ii)对称的无迹张量的向量空间是同构的，并且假定它们各自的内积在这些轴线的任何旋转下是对称的，这样使得它们可以说成是作用于这些张量本身上，而不仅仅是作用于一个坐标系中的它们的分量上，如下的这两个内积也是同构的是合理的：(i)被写为《,》的张量内积，以及(ii)等式47中定义的球面内积《,》s。即，直到微不足道的秩相关归一化因子，n
(n)
：
[0257]
《h
a(n)
,h
b(n)
》s＝n
(n)
《h
a(n)
,h
b(n)
》
ꢀꢀꢀꢀꢀ
(51)
[0258]
其中是调和多项式h
(n)
(r)的无迹张量表示。
[0259]
根据内积同构，那么等式49中定义的q
i(n)
对称张量形成秩n的无迹张量的完整正交基，从而使得假设适当的归一化：
[0260]
《q
i(n)
,q
j(n)
》＝δ
i,j
ꢀꢀꢀꢀꢀ
(52)
[0261]qi(n)
提供这样的基允许根据下式将任何对称的无迹秩n张量表达为秩n球谐函数的和：
[0262][0263]
并且取等式53的两侧关于q
i(n)
的内积，示出了球谐基中的a
(n)
的分量，由以下给出：
[0264][0265]
其中球谐分量由现代罗马小写字母索引，而不是笛卡尔索引的希腊字母。
[0266]
根据等式54的无迹张量从笛卡尔到球谐函数的转换也许最容易通过查阅球谐函数多项式的表来完成。并且为了方便起见，表i中列出了上至秩3的球谐函数多项式。
[0267]
作为示例，从表i中，我们具有给出的球谐函数，并且假定其给出了其给出了等等。
[0268]
球谐函数表示对于计算内积尤其有用；通过使用球谐函数的正交性来写：
[0269][0270]
因此，可以看出，计算球谐函数中的内积需要针对该秩的最小2n+1次运算，这比将所有矩阵笛卡尔分量一起自然地相乘所需的3n次乘法是节省了大量时间。
[0271]
现在已经证明了系数如何允许将笛卡尔变换成球谐函数。还存在由给出的逆变换，它们是投影到球谐函数基上的的分量，且其可用以将球谐函数基中的分量变换回到笛卡尔。
[0272]
表ii提供了用于进行这些变换的表方便的方式。
[0273]
作为示例，表ii给出了由此得出，具有球谐分量有球谐分量
[0274]
接下来，我们考虑去迹算符。
[0275]
假设t
(n)
是一般非无迹的对称张量。假定球谐函数为无迹秩n张量的子空间形成完整正交基，则投影算符可由下式形成：
[0276][0277]
其中起到将张量投影到无迹子空间中的作用，使得上述结果是无迹张量。因此，
是去迹算符。
[0278]
尤其值得注意的是的一种应用。从霍普森定理可以看出，来自等式24的麦克斯韦笛卡尔球谐函数，s
(n)
，是r
(n)
张量的无迹形式，由此得出然后，将以上表达式应用于并且使用等式50进行取代《r
(n)
,q
i(n)
》＝q
i(n)
(r)，意味着：
[0279][0280]
由此，麦克斯韦笛卡尔球谐函数的球谐分量仅为球谐多项式本身。
[0281]
球谐函数中的多极相互作用
[0282]
本部分的目的是将迄今为止在笛卡尔中开发的各种表达式转换成它们的球谐函数等同物。
[0283]
在最后一部分中，示出了如何将内积转换成球谐函数。并且在此方面，令人遗憾的是，等式31的多极相互作用生成公式不能完全根据这些乘积来表达，因为它涉及形式的有问题的收缩。
[0284]
然而，即使当处理这种收缩时，存在一种仍使用内积方法的方式，现在将对其进行描述。
[0285]
现在将使用符号引入对称张量的分裂分量表示，其中n＝na+nb是张量的满秩，其只是一个表示。以na＝3、nb＝2为说明性示例，具有笛卡尔分量的对称无迹多极张量m
(3,2)
可以写为：
[0286][0287]
其中m
(3,2)
相对于以下内容变换为对称的无迹笛卡尔张量：(i)其逗号前的分量，(ii)其逗号后的分量，以及(iii)在其作为整体的所有分量中。使用该表示，示例收缩现在可被写为：
[0288][0289]
其相对于逗号后分量表现像内积，并且因此，可以在球谐函数中容易地计算。
[0290]
通过将的逗号前分量和逗号后分量分别变换为球谐函数，并且使用等式43描述的种类的变换，给出：
[0291][0292]
其中用于变换并且用于变换并且如在最后一部分中所讨论的，这些变换最容易通过球谐函数的表来进行，适当地实现成代码。
[0293]
同样，并且参考等式56的去迹算符的讨论，r
(n)
张量分量被变换为并且因此所希望的收缩现在可以用球谐函数写为：
[0294][0295]
注意，分裂分量表示的概念可以相当普遍。有可能使用混合的笛卡尔-球谐函数表示，如或可以使用多于一个表示；例如，是m
(6)
的有效分裂。然而，无论如何选择分裂或基础，其仍然指代相同的底层张量，并且如果必要的话，人们可以总是通过采取适当的逆变换来从中恢复所有的原始分量。
[0296]
秩1球谐函数仅是x、y和z(见表i)，从其得出秩1张量具有与笛卡尔相同的球谐分量并且，通常，
[0297]
分裂分量表示关于其分量的任何排列是对称的，例如以及等等。
[0298]
这些变换都可以通过在最后部分中解释的表方法来完成。也就是说，不必执行繁琐的矩阵乘法，而是可改为仅使用适当地实施为代码的表i以将笛卡尔转换为球谐分量。
[0299]
在这个阶段，返回到图形表示将证明是有用的。
[0300]
图8示出了球谐函数和笛卡尔坐标中的张量的不同表示之间的等效。给出的例子是无迹对称秩4张量，示出为节点400，其可表示为t
(1,1,1,1)
(400a)或t
(2,1,1)
(400b)、或t
(2,2)
(400c)、或t
(3,1)
(400d)、或t
(4)
(400e)，其中笛卡尔坐标，通常由辐条332表示，并且其中到球谐函数的变换是通过将任何数量的辐条编织在一起来描绘的。当然，这仅是视觉象征，但是其旨在传达至球谐函数的变换如何将多个笛卡尔指数(通过采用线性组合)交织成一个球谐函数指数。
[0301]
参见图9a，示出了图4中所描绘的能量项，参见图9a，示出了图4中所描绘的能量项，如何可以通过执行编织以及以及然后根据以下公式计算收缩，而转换成球谐函数：
[0302][0303]
并且在图5底部的最终图解等式示出了如何将以上项的梯度转换成球谐函数，这需要附加编织
[0304]
在此开发的方法可以用于变换任何收缩，并且因此，我们现在处于将整个多极相互作用、能量和力和场变换成球谐函数的位置。我们从等式31的多极相互作用生成公式开
始，等式31在球谐函数中由下式给出：
[0305][0306]
与等式34的球谐函数模拟(其给出力计算所需的梯度项(每个等式33))由下式给出：
[0307][0308]
并且与等式25的球谐函数模拟(其给出多极场(每个等式24)所必需的导数)由以下等式给出：
[0309][0310]
这个最后的表达式需要一些解释。和中的每个项具有类型的张量表示，但假定是对dc,dj求和，方括号中的量将导致不同分裂分量表示中的和，例如，对于秩4，该和将具有形式s
(4)
＝c4t
(4)
+c
3,1
t
(3,1)
+c
2,2
t
(2,2)
，其中这些表示一般不是指对称的张量。然而，一旦已经评估出全和，就可以在对笛卡尔索引的所有排列进行平均之前，通过将结果转换回笛卡尔来对称。
[0311]
来自原点处的多极展开的在r处的静电势可以从以上通过取秩0多极导数然后使用等式37而求出以获得
[0312][0313]
其中最后一项可以从第一项导出，或从取等式38的秩0多极导数获得，并且其中我们注意到，对于内核，它减少到等式11。
[0314]
最后，给出多极位点上的总扭矩的等式41的球谐模拟由下式给出：
[0315][0316]
等式63-67于是包括用于在球谐函数中的多极相互作用的最终表达式，其形式适合于实施成埃瓦尔德和。在此，我们应该承认，我们没有针对多极的旋转或针对角导数的计算(等式40)给出球谐函数。为了简单起见，优选在笛卡尔里保持这些，但是考虑到可以在主ij粒子回路之外执行这两个计算，所以它们的计算没有显著的计算成本。
[0317]
作为一个示例，使用超晶胞法和晶体结构预测算法来预测在不同外部压力下的水的4位点tip4p经验分子模型的最低焓结构。结果显示在图3a至3l中。
[0318]
通过对所有原子间对求和来给出此模型的能量，其中ij对的能量由下式给出：
[0319]
[0320]
其中a
12
和a6是常数。tip4p是刚性水模型，具有由hoh角、θ
hoh
和oh键距离r
oh
确定的固定几何结构。它在每个水的氧位点上具有单个lennard jones相互作用位点，在氢原子上具有电荷qh，并且在无质量
‘
m-位点’上具有-2qh的电荷，该无质量
‘
m-位点’被放置在分子平分线上，在从氧核朝向h核的r
om
的距离处。模型参数在表3中给出。
[0321]
通过对三斜晶周期晶胞实施埃瓦尔德和来处理静电相互作用，其中使用超晶胞技术将该和的实空间部分与lennard jones相互作用求和，发现其足够好以将每模拟晶胞的能量收敛至约十分之一的kj/mol。和的倒易空间部分不受超晶胞方法的影响，并且以标准方式实施。
[0322]
为了防止截止处的不连续性，将lennard jones对相互作用乘以s形三次平滑阶跃函数s(x)，其从s(x)＝1；x《0.9rc到s(x)＝0；x》rc平滑地插值。通过实施此函数，可以适当地修改u
lr
长程能量(等式2)的表达式为使得积分是从0.95rc至∞。
[0323]
埃瓦尔德和的实空间部分涉及在形式的高斯电荷分布上进行求和，并且该和的倒易空间部分涉及在其傅里叶变换对上进行求和：，其中∈是自由选择的参数，该参数确定埃瓦尔德和的收敛。为了确保良好的收敛，我们希望g(r)在真实空间截止处非常小，并且我们还将在倒易空间kc中选择截止，使得g(k)在kc处类似地较小。为此，我们选择ζ和kc为使得
[0324]
∈＝g(rc)＝g(kc)
ꢀꢀ
(69)
[0325]
其中δ是一个非常小的数。在当前情况下，δ＝10-7
。
[0326]
上式求逆给出：
[0327][0328]
以及
[0329]
kc＝2ζ2rcꢀꢀ
(71)
[0330]
全部使用定制的内部代码来进行计算，但是对照标准分子动力学包检查能量，以确保结果是正确的和可重复的。
[0331]
使用数字配方1(numerical recipes1)的frprmn子程序来进行局部优化，该子程序是fletcher-reeves共轭梯度算法的实施。
[0332]
盆地跳跃实现方式使用从高斯分布绘制的步骤，其中对于每个分数质心坐标有σf＝0.08的西格玛值，对于每个欧拉角，σe＝1弧度，以及对于六个独立晶胞向量分量中的每一个，每个蒙特卡罗步骤包括首先随机选择一分子，然后对该分子进行随机平移和旋转，结合所有六个晶胞向量分量中的随机位移。发现250k的温度对于metropolis monte carlo验收标准接近最佳。
[0333]
即使使用良好的算法，定位全局最小值也是一个难题。为了证明实际找到全局最小值的最佳机会，对于每种情况，使用多个独立的盆地逃脱模拟，每个从不同的随机初始配置开始，并且使用不同的随机数种子用于蒙特卡罗位移。总的来说，24个独立的盆地逃脱轨迹的群体用于每个结构，其各自在单独的核上运行。这用于有效地并行化问题，并且还用于增加搜索的多样性，考虑到个体行走可能在长时间内高度相关，所以多样性是关键问题，因为个体行走可能被困在低的最小值的漏斗中。
[0334]
使用独立轨迹的另一个优点是，如果从不同初始条件开始的多个轨迹中发现相同的最低最小结构，则其给出了推定的全局最小值可能是正确的某种保证。
[0335]
在当前情况下，计算最佳(即，最低焓)结构的范围，其中最佳候选有希望地包括真实的全局最小结构。为了实现这一点，存储在每个准蒙特卡罗行走的过程中所接受的每个最小值以形成候选最小值列表，该候选最小值列表可以稍后被排序和排名。
[0336]
图3a至3l中示出了示例结构。每个结构302-324表示用于冰的可能的晶体结构。如下面进一步详细描述的，每个结构包含一系列氢键(h-键)，其有助于在多种可选的冰多晶型物中定向水分子。
[0337]
许多冰多晶型物是质子无序的。即，对于给定的氢键构型，质子的位置可以采用任何数量的可能的构型，同时仍然遵守冰规则。考虑到这一点，本工作对找到仅达到质子有序的最佳(即，最低焓)结构感兴趣，使得仅计算为每种不同类型的氢键网络找到的最低焓结构。
[0338]
对于每个最小能量结构，产生h键的列表，其中如果两个水分子的oo距离小于并且h-o
‑‑
h角小于30度，则认为这两个水分子是氢键的。
[0339]
然后任务是要知道两个结构是否共享相同的氢键网络。这是一个非常重要的任务，基本上等同于决定两个图形的同构的图形理论问题。(部分)解决方案是进行每个最小能量结构的环分析，其中创建存在于该结构中的水四聚体、五聚体、六聚体等环的列表。每个环是水分子的氢键回路，其中仅列出了不能进一步分解成更小环的那些环。
[0340]
注意，这不是完全的解决方案，因为可能的是两个结构每单胞可以具有相同数目的分子，有相同的环分解，但具有不同的氢键网络。然而，这是本案例中的方法。
[0341]
这种环分解允许人们开发命名方案，其中用它们的环数目和每单胞的分子数目标记结构。在这个方案中，例如结构s12/5864788
8-312每单胞具有12(
‘
s’后面的数字)个分子。在正斜线之后的数字给出了环计数，并且这种结构具有八个五元环、四个六元环、八个七元环以及八个八元环。在图3a至3l所示的每个图中，方框示出了单胞，该单胞然后根据上述方法用作模拟晶胞。
[0342]
在本案例中，计算高达10元环的环分解。
[0343]
在周期性边界条件中并且在0巴、4000巴和8000巴的压力下，在1-14个tip4p水分子的范围内进行系统性搜索。
[0344]
搜索找到了数百个结构，但表4a、4b和4c列出了在每个压力下发现的十个最佳(最低焓)结构，最佳结构的选择在图3a至图3l中示出，并且所有结构的坐标在补充信息中提供。
[0345]
转到表4a，在零压力下，最佳结构被束缚在冰ic与冰ih结构(结构s4/6
8 302和s8/6
16 308)之间，这些结构具有(至此精度)-57.104kj/mol(每分子)的相同能量。
[0346]
注意，还发现了具有甚至更小的单胞的冰晶格。晶体结构预测代码的确仅使用两分子的模拟晶胞定位了冰ic晶格，并且仅使用四分子的模拟晶胞定位了冰ih晶格。然而，这两者的能量都高于以更大晶胞所能发现的能量，推测是由于更大的单胞提供了更好的质子排序。
[0347]
所发现的第三最佳结构是冰iii结构，s12/5
87888 304，其在能量上比最佳冰ih和冰ic结构仅高0.3kj/mol。
[0348]
这些结构的排序在4000巴下完全改变，并且查看表2b，在这个更高的压力下，冰ih和冰ic结构不再是最好的十个，并且冰iii结构304现在是具有最低焓的结构。冰vi结构
s10/4
10818 316也位于前十之外。
[0349]
最后，在8000巴下，冰iii结构304仍然处于第一位置，但是晶体结构预测算法也位于第三位置，冰xii结构，s6/788
12 320，正好在s12/42688
22
10
30 314后面，其似乎不是已知的多晶型物之一。冰vii结构s2/6
4 324也位于前十之外，它是由两个相互穿插的冰ic晶格组成的高压相。
[0350]
发现每分子具有最低能量的两个零压力晶体结构：冰ic结构302，具有四个分子的最小单胞；以及冰ih结构308，具有八个分子的最小单胞，两个结构具有接近相同的能量(至五个有效数字)。
[0351]
冰ic 302和冰ih 308的能量非常接近不是太令人惊讶，因为它们都是具有围绕每个分子的几乎相同的四面体配位的第一相邻壳的冰结构。然而，令人惊讶的是，发现的最佳结构似乎具有几乎相同的能量。然而，这些结构的密度确实不同(然而稍微不同)，所以怀疑它们的能量的一致性是数字巧合的结果，而不是因为任何更深的物理原因。实际上，发现略微改变模型电荷或施加外部压力足以破坏一致性。
[0352]
在下文中，使用盆地跳跃算法预测三种不同有机分子(即，苯、分子xxii和d-甘露醇，在图10中示出)的晶体结构。
[0353]
该方法考虑以下四个步骤：
[0354]
1.目标分子的构象偏好的探索
[0355]
对于苯，仅存在一种构象异构体，而对于分子xxii，我们观察到两种构象异构体，它们是彼此的镜像。对于甘露醇，使用沿着50ps的轨迹的单个分子的从头开始分子动力学模拟来探索该分子的所有可能的分子构象。然后考虑相等间距的2500个几何结构-每个几何结构使用b3lyp/6-31g(d)的理论水平。考虑到甘露醇的优化能量和正常模式，区分甘露醇的104个构象异构体。因此，产生了目标分子的可能构象异构体库的列表。
[0356]
2.力场参数的发展
[0357]
考虑具有4个分子的正交盒(使用从头开始npt模拟来近似盒的体积)，然后nvt模拟进行了50ps，这用192cpu花了大约一个月的时间。然后使用所得轨迹来拟合经验势能表面，其中总分子间势能被定义为(i)静电项(其使用高达八极-八极的原子多极相互作用来处理)以及(ii)成对添加原子间相互作用的和，成对添加原子间相互作用使用径向函数以形式u＝a/r4+b/r8+c/r
10
的逆幂级数来建模，其中r是原子间间距，并且a、b和c是参数。
[0358]
通过使用
‘
力匹配’算法的变型来确定参数，其中参数被优化以最佳地再现每个分子的质心力上的dft力和在轨迹的过程上围绕质心的dft扭矩。该系统的总分子间能量也被考虑在内。此处的原理是仅适合对分子内贡献不敏感的特性，其是质心上的力、以及围绕那些质心的扭矩。
[0359]
不同原子之间的相互作用通常非常不同，例如，h和o原子之间的相互作用将与两个h或两个o之间的相互作用非常不同，因此必须为每种不同的相互作用类型选择单独的a、b、c参数。发现甚至相同原子类型之间的相互作用高度依赖于其局部化学环境。出于这个原因，不仅通过在对中涉及的原子的类型而且通过该对的每个成员键合的原子来区分这些相互作用。因此，例如，键合到o的h被计算为与键合到c的h不同的类型。由此产生的不同相互作用类型的数量是相当大的，使得典型地处理约100个不同的径向函数的级数以模拟30个原子的分子间相互作用，这进而意味着存在约300个要拟合的参数。但是力匹配可以处理这
一点，并且可以在大约几分钟内找到所有这些参数。
[0360]
如上所述，使用多极方法评估静电相互作用。在这种方法中，使用gdma软件(版本2.2.11)计算气相中的分子的原子电荷分布的多极展开，该gdma软件发现了描述由电子结构电荷分布产生的静电势的原子多极系数，给出了比传统点电荷模型优越得多的描述。
[0361]
然后，使用来自多极理论的表达式，通过对每个多极之间的静电相互作用求和来计算具有经验模型的分子间能量的静电分量。在本发明中，将这个和扩展到八极-八极水平，这应该给出静电学的非常精确的说明。
[0362]
3.生成目标分子的合理晶体堆积排列
[0363]
本发明中公开的盆地跳跃方法用于探索可能的晶体堆积排列。总之，一旦构建了经验模型，问题是找到具有该经验势能表面的最佳晶体结构。这通过实质上在周期性边界条件中搜索最小能量构型并且找到具有最低能量的最小值来完成。这证明是困难的挑战，因为可能的最小值的数量可能是巨大的，因此需要使用具有在合理的时间内定位最低能量最小值的机会的
‘
全局优化’算法。这里使用所谓的
‘
盆地跳跃蒙特卡罗(basin-hopping monte-carlo)’全局优化算法。
[0364]
标准蒙特卡罗算法在构型空间上执行随机行走，基于它们相对于先前一步的能量差而接受或拒绝移动，其可以被示出为在长时间限制内产生正确的结构热分布。
[0365]
basin-hopping monte-carlo算法是原始monte-carlo算法的修改，其中针对行走中的每个点处的局部最小值的能量来进行接受/拒绝步骤。即，在接受和拒绝新结构之前，系统通过优化算法被放松至其局部最小值，并且其是用于确定是否接受新结构作为蒙特卡罗
‘
行走(walk)’中的下一个结构的最小值的相对能量。在蒙特卡罗的每一步引入局部优化使行走减慢，可能减慢一个数量级，但是也发现产生了在克服最小值之间的障碍方面好得多的行走，因此在定位低的最小值方面好得多。
[0366]
4.构象异构体搜索
[0367]
到目前为止，仅讨论了分子间相互作用，但是真实分子是柔性的，并且如果要预测正确的晶体结构，则必须考虑这种柔性。在本研究中，使用基于构象异构体的方法。首先，用气相构象异构体几何结构构建库，对应于单分子的dft表面上的局部最小值。然后，在本实施中将分子视为刚性的basin-hopping monte-carlo模拟被允许在每次行走的过程中在不同的构象异构体之间
‘
翻转(flip)’。即，模拟晶胞中每个分子的几何结构总是设置为等于构象异构体库中的构象异构体之一，但是引入蒙特卡罗移动，其中每个分子具有翻转成不同构象异构体的机会，具有如通常由翻转前后(松弛的)周期性结构的能量差确定的概率。
[0368]
5.将得到的预测晶体结构排序
[0369]
使用高级dft计算对预测的晶体结构进行重排序。对于每个分子，考虑使用basin hoppling方法预测的50个最低能量晶体。注意，考虑basin hopping方法中的刚性分子。使用色散校正的dft方法放松原子位置和晶格向量两者。这种放松提高了我们预测的晶体的可靠性。
[0370]
计算细节
[0371]
如在cp2k包的quickstep模块中实施的，使用具有perdew-burke-ernzerhof(pbe)1泛函和gpw形式化的密度泛函理论(dft)进行从头开始分子动力学模拟(npt和nvt两者)。规范守恒goedecker-teter-hutter(gth)赝势与连同双zeta价极化(dzvp)基组一起使用以
扩展kohn-sham价轨道，其中能量截止值为320ry，具有周期性边界条件。使用grimme(dft-d3)方法考虑非共价范德华相互作用。
[0372]
为了探索分子的所有可能的分子构象，沿着50ps的轨迹进行单个分子的从头开始分子动力学模拟。使用b3lyp/6-31g(d)理论水平，考虑相等间隔的2500个几何结构并优化每个几何结构。考虑到它们优化的能量和正常模式，优化的几何结构是有区别的。
[0373]
为了对预测的晶体进行排序，使用具有平面波基础的dft(具有400ev的平面波能量截止值)和用于perdew、burke和ernzerhof(pbe)的版本中的交换相关能量函数的一般梯度近似(gga)，几何结构与晶格弛豫一起被重新优化。
[0374]
结果和讨论
[0375]
1.探索目标分子的合理构象
[0376]
对于苯，仅存在一个构象异构体，而对于分子xxii，观察到两个构象异构体，它们是彼此的镜像。对于甘露醇，使用沿着50ps的轨迹的单个分子的从头开始分子动力学模拟来探索该分子的所有可能的分子构象。从50ps从头开始的轨迹中考虑相等间隔的2500个结构，并使用b3lyp/6-31g(d)理论水平优化每个结构。
[0377]
2.将得到的预测晶体结构排序
[0378]
在多个处理器上并行执行独立的basin hopping monte carlo运行，以产生数万个推定的晶体结构最小值。然后过滤这些结果以找到最低的最小值。然后使用高级dft计算对预测的晶体结构进行排序，即，从basin hopping monte carlo取得预测的最佳结构，然后在全dft势能表面下重新松弛这些结构。考虑了针对每个分子使用basin hoppling monte carlo法预测的50个最低能量晶体。在图11中，dft能量相对于力匹配能量绘制如下。
[0379]
3.预测的晶体结构与试验晶体结构之间的比较
[0380]
将苯、xxii和d-甘露醇的预测晶体结构与图12a-c中的试验预测结构进行比较。预测的晶体与试验晶体具有很好的可比性，具有空间群等效性。
[0381]
表i.达到秩3的笛卡尔中的球谐函数q
i(n)
(r)。
[0382]
球谐函数被归一化，从而使得||q
i(n)
||＝1，其中q
i(n)
是q
i(n)
(r)多项式的张量形式。
[0383]
秩0
[0384]qi(0)
＝1
[0385]
秩1
[0386]q1(1)
＝x
ꢀꢀq2(1)
＝y
ꢀꢀq3(1)
＝z
[0387]
秩2
[0388][0389][0390]
秩3
[0391][0392]
[0393][0394]q6(3)
＝(1/2)x(x
2-3y2)
[0395]q7(3)
＝(1/2)y(3x
2-y2)
[0396]
表ii.根据球谐函数的笛卡尔，高达秩3
[0397]
秩2
[0398][0399][0400][0401]
秩3
[0402][0403][0404][0405][0406][0407]
表3：水的tip4p模型的模型参数。同样，注意所报告的密度是使用(略微理想化的)原子质量mh＝m
p
、mo＝16.0m
p
以及mm＝0计算的，其中m
p
是质子质量：m
p
＝1.67262178*10-27
kg。
[0408][0409]
表4a：在0巴下每分子结构的十个最低焓，连同它们的焓和密度。
[0410][0411][0412]
表4b：在4000巴下每分子结构的十个最低焓。还示出了冰vi结构，s10/4
10818
。
[0413][0414]
表4c：在8000巴下每分子结构的十个最低焓。还示出了冰vii结构，s2/64。
[0415][0416]
在另外的或替代的实施例中，以及优化描述每个分子的位置的自由度，对于具有经验模型电势的晶体结构预测，考虑分子柔性也是有用的。
[0417]
即使忽略分子内自由度，在分子内和分子间几何结构之间可存在相互作用，使得大尺度晶体结构可取决于单个分子的几何结构可如何扭曲。
[0418]
不幸的是，设计可以准确地描述单个分子可以如何扭曲的分子内电势是非常困难的。然而，可以求助于近似。本实施例中使用的主要近似是通过其局部最小值来表示整个分子内势能表面，即通过每个单独分子的可能的局部最小值结构的几何结构和能量。
[0419]
一般策略如下：首先构建感兴趣分子的局部最小值的代表性数据库，记录这些最小值的能量和几何结构。然后，通过
‘
构象空间’找到从一个最小值跳到另一个最小值的某种方式。这可以作为以上描述的较大晶体结构预测算法的一部分来进行，使得算法不仅在描述每个分子的位置的通常自由度上进行优化，而且在每个分子的构象空间中进行优化，希望找到这样的晶体结构：所述晶体结构对于构成分子的所有可能排列和所有可能构象异构体是最小能量构型。
[0420]
于是第一个任务是获得构象异构体最小值(及其相关几何结构)的库。这通过运行气相中分子的密度泛函理论(dft)轨迹，由此产生优化(以固定长度间隔，例如每100步)。通过能量和对角惯性矩对得到的结构进行排序，以去除重复。
[0421]
接下来的任务是找到一种识别类似构象异构体的方式，其帮助定义通过最有效地行走的构象异构体空间的路径。这通过计算原子核的相对均方位移(msd)来完成。
[0422]
两个构象异构体m和n之间的msd由下式给出：
[0423][0424]
其中是第m个构象异构体中第i个核的笛卡尔坐标。wi是权重因子，其可以被设置为一，或者可以被选择为将不同的重要性分配给不同的核。在当前情况下，wi＝mi，其中mi是第i个核的质量。
[0425]
由于m坐标和n坐标都描述刚性分子几何结构，所以msd是三个平移自由度和三个旋转自由度的函数。可以通过坚持这三个平移自由度都被放置成使得它们的质心与原点重合来消除这三个平移自由度。然后，仅剩下三个旋转自由度，这可以通过三个欧拉角φ、θ和ψ来描述。为此，可以定义：
[0426][0427]
其中可以被认为是构象异构体n的身体中心坐标，并且其中r(φ，θ，ψ)是由欧拉角定义的3x3正交旋转矩阵。因为仅相对取向是重要的，所以仅需要考虑该对中的一个的旋转，并且因此因此，msd由下式给出：
[0428][0429]
为了找出哪些欧拉角最小化了总msd，使用共轭梯度算法，其将需要关于欧拉角的角导数。这些由下式给出：
[0430][0431]
并且对于θ和ψ是类似的。
[0432]
共轭梯度优化的结果是对于每个m-n对，可以找到关于欧拉角的最小msd为：
[0433]
min[msd
m,n
]＝μ
m,n
ꢀꢀꢀꢀꢀꢀ
(76)
[0434]
其中μ
m,n
是具有相关联的欧拉角的矩阵元素。
[0435]
μ
m,n
矩阵元素告诉我们每对构象异构体之间的最小msd是什么，但是仍然需要如何在构象异构体之间步进的规则。在本案例中的方法是定义具有元素p
m,n
的随机矩阵，该随机矩阵给出了在构象异构体翻转步骤上从构象异构体m
→
n翻转的概率，其中p
m,n
是μ
m,n
个矩阵元素的某个函数，使得在具有更小msd的构象异构体之间翻转的概率更大。不存在这样做的独特方式，然而，在当前情况下，该方法将选择：
[0436]
[0437]
其中β是一个自由选择的参数，该参数像一个逆温度一样起作用，并且其中可以验证这些概率总和为一：
[0438][0439]
当β
→
0(高温)时，概率相等，具有与任何其他构象异构体一样可能访问一个构象异构体的步骤，并且当β
→
∞(即，温度变为零)时，步骤仅对于相对于起始构象异构体具有最低msd的构象异构体是可能的。
[0440]
在实践中，β应当被选择为使得涉及低的相对msd的步骤是有利的，但是在虚构温度足够高的情况下，该系统最终将以合理的概率访问每个构象异构体。
[0441]
在模拟过程中特定构象异构体的坐标可以表示为三个com坐标，以及三个有理坐标，再次由欧拉角给出，其被标记为(φ0,θ0,ψ0)。现在，假设允许特定的构象异构体从m
→
n翻转，并且我们想要更新其欧拉角，使得它在翻转之前和之后经历最小的msd变化。这可以通过首先找到旋转矩阵r0＝r(φ0,θ0,ψ0)，然后找到旋转矩阵并且然后找到复合旋转矩阵来完成，然后可以将其求逆以获得(φ0,θ0,ψ0)的新值。
[0442]
构象异构体搜索算法很容易结合到盆地跳跃蒙特卡罗型算法中。这通过随机选择一定百分比的蒙特卡罗步骤以涉及随机挑选分子，然后根据随机矩阵中的概率将该分子的构象异构体翻转成另一构象异构体来进行，所述概率已经事先得出。
[0443]
早期构建构象异构体的数据库的方法不保证是穷举的。然而，可以迭代构象异构体搜索的整个过程然后进行晶体结构预测，使得(最后)可能找到正确的构象异构体。这可以通过首先构建构象异构体的初始数据库来完成，然后将其用于晶体结构预测运行。然后可以在dft下放松由此运行得到的最佳结构，以产生可以扩充到构象异构体数据库中的新的构象异构体，为更多的晶体结构预测步骤做准备，等等。
[0444]
通过阅读本公开，其他变化和修改对于本领域技术人员将是明显的。此类变化和修改可涉及晶体结构确定领域中已知的等效和其他特征，并且这些特征可用于替代或补充本文已描述的特征。
[0445]
尽管所附权利要求书针对特征的特定组合，但应理解，本发明的公开范围还包括在此明确地或隐含地公开的任何新颖特征或特征的任何新颖组合或其任何概括，其是否涉及与任何权利要求中当前要求保护的相同的发明以及其是否缓解与本发明所做的相同的技术问题中的任何一个或全部。
[0446]
在单独实施例的上下文中描述的特征也可以组合地提供在单个实施例中。相反，为了简洁起见，在单个实施例的上下文中描述的不同特征也可以分开地或以任何合适的子组合来提供。本技术人特此注意到，在本技术或由其衍生的任何进一步申请的审查期间，可以针对此类特征和/或此类特征的组合制定新的权利要求。为了完整起见，还陈述术语“包括”不排除其他元件或步骤，术语“一个”或“一种”不排除多个，单个处理器或其他单元可以实现权利要求中列举的若干装置的功能，并且权利要求中的参考符号不应被解释为限制权利要求的范围。