海杂波Pareto分布模型的参数估计范围拓展方法与流程

本发明属于雷达信号处理技术领域，尤其涉及一种海杂波Pareto分布模型的参数估计范围拓展方法，可用于目标检测。

背景技术：

参数估计一直是信号与信息处理领域的核心问题。海杂波的K分布模型由于其合理的理论解释与很好的实际拟合受到了众多学者的广泛关注。然而，在海尖峰强烈时，K分布模型在其拖尾处往往不能很好地拟合实际海杂波，KA与KK分布虽然能够较K分布更好地拟合实测海杂波，但也由于引进的新分量带来了更多的参数估计要求而影响了雷达目标检测的实时性。

近年来的许多文献与研究指出，Pareto分布是一种较K、KA及KK分布更有优势的雷达杂波模型，它不但在拖尾处更好的拟合了实测数据，而且根据该分布设计的雷达目标检测器具有更简洁的形式。在实际的雷达目标检测中，往往需要对一个相干处理间隔CPI内的N次观测信号进行相参或非相参积累以实现高的信杂比，因此对N次观测的Pareto分布参数进行准确估计对海杂波背景下的目标检测性能具有重要意义。

传统的对海杂波单次观测Pareto分布模型进行参数估计主要有如下四种方法：

1.最大似然估计法。此方法可以有效估计海杂波的各项参数，但是在对其大部分参数进行估计时，计算过程非常复杂，计算效率低下，不能保证实时性。

2.正整数阶矩估计法。以常用的一二阶矩估计法为例，此方法计算简便，但在对形状参数进行估计时，需要调用Gamma函数，而Gamma函数在参数真值小于2时无意义，因此该方法不能有效估计小于2的形状参数。

3.基于<zlog(z)>的方法。该方法在对形状参数进行估计时，与一二阶矩估计法相比，能将有效估计范围扩展到真值大于1的情形，但是此方法在计算过程中需要调用Diagram函数，而Diagram函数在参数真值小于1时无意义，因此该方法不能有效估计小于1的形状参数。

4.分数阶矩估计法。此种方法将传统的矩估计法扩展到分数范围，可以有效估计所有范围内的形状参数，但是计算结果不能得到闭合表达式，需要用复杂的数值运算寻找方程零点，计算效率低下，不能保证实时性。

技术实现要素：

本发明的目的在于针对上述已有技术的不足，提出一种基于闭合表达式的海杂波Pareto分布模型的参数估计范围拓展方法，以在提高运算效率的同时，解决参数有效估计范围受限的问题，保证雷达目标检测的实时性。

实现本发明目的的技术方案是：首先建立海杂波的Pareto分布模型，通过Pareto分布的概率密度函数推导出N次Pareto分布随机样本数z的r阶原点矩，将矩估计扩展到负数阶矩范围，采用负整数阶矩对N次观测Pareto分布进行估计并得出闭合的估计表达式，具体步骤包括如下：

(1)根据海杂波的复合模型理论，建立海杂波的Pareto分布模型f_N(z)；

(2)利用海杂波N次观测的Pareto分布概率密度函数，推导出海杂波的实际观测值z的r阶原点矩估计表达式为其中，α为海杂波模型的形状参数，β为海杂波模型的尺度参数，α>0，β>0，z≥β，N为观测次数或脉冲积累次数，r为阶数，Γ(·)表示Gamma函数；

(3)将r取值扩大到负数范围，对海杂波模型的形状参数α进行估计：

(3a)为避免β的指数幂对计算效率的影响，分别取r＝-M₁与r＝-M₂，记为z的-M₁阶原点矩，为z的-M₂阶原点矩，对和进行求幂的比值运算，消去β的指数幂，得到如下表达式为：

$\frac{\&lt;z^{-M_1}{\&gt;}^{M_2}}{\&lt;z^{-M_2}{\&gt;}^{M_1}}=\frac{{\mathrm{\&Gamma;}}^{M_2}(N-M_1){\mathrm{\&Gamma;}}^{M_2}(\mathrm{\&alpha;}+M_1){\mathrm{\&Gamma;}}^{M_1}\left(N\right){\mathrm{\&Gamma;}}^{M_1}\left(\mathrm{\&alpha;}\right)}{{\mathrm{\&Gamma;}}^{M_1}(N-M_2){\mathrm{\&Gamma;}}^{M_1}(\mathrm{\&alpha;}+M_2){\mathrm{\&Gamma;}}^{M_2}\left(N\right){\mathrm{\&Gamma;}}^{M_2}\left(\mathrm{\&alpha;}\right)}---\&lt;1\&gt;$

其中，M₁和M₂为正整数，N-M₁>0，N-M₂>0；

(3b)根据Gamma函数的性质，对于任意正整数i和j有:

Γ(i)＝(i-1)(i-2)…(i-j)Γ(i-j) <2>

其中，i>j；

根据式<2>，对式<1>进行化简，得到如下闭合表达式为：

$\frac{\&lt;z^{-M_1}{\&gt;}^{M_2}}{\&lt;z^{-M_2}{\&gt;}^{M_1}}={\left(\frac{(\mathrm{\&alpha;}+M_1-1)(\mathrm{\&alpha;}+M_1-2)...\mathrm{\&alpha;}}{(N-1)(N-2)...(N-M_1)}\right)}^{M_2}\&CenterDot;{\left(\frac{(N-1)(N-2)...(N-M_2)}{(\mathrm{\&alpha;}+M_2-1)(\mathrm{\&alpha;}+M_2-2)...\mathrm{\&alpha;}}\right)}^{M_1}---\&lt;3\&gt;;$

(3c)为简化运算，取M₁＝1、M₂＝2代入式<3>，得到用z的负一阶原点矩和负二阶原点矩估计α的表达式为：

$\frac{\&lt;z^{-1}{\&gt;}^2}{\&lt;z^{-2}\&gt;}={\left(\frac{\mathrm{\&alpha;}}{N-1}\right)}^2\&CenterDot;\frac{(N-1)(N-2)}{(\mathrm{\&alpha;}+1)\mathrm{\&alpha;}}---\&lt;4\&gt;$

其中，<z^-1>为z的负一阶原点矩，<z^-2>为z的负二阶原点矩；

(3d)将式<4>进行整理，得到α的最终估计表达式为：

$\mathrm{\&alpha;}=\frac{(N-1)\&lt;z^{-1}{\&gt;}^2}{(N-2)\&lt;z^{-2}\&gt;-(N-1)\&lt;z^{-1}{\&gt;}^2}---\&lt;5\&gt;;$

(4)当观测次数N>2时，用式<5>估计形状参数在α∈(0,+∞)范围内的Pareto分布参数，完成对海杂波Pareto分布模型的参数估计范围的扩展。

本发明与现有技术相比具有如下优点：

1.与传统的正整数阶矩估计法相比，由于本发明将矩估计的阶数范围扩大到负整数阶矩，因而在观测次数N>2时，能够有效扩大海杂波形状参数的估计范围；

2.与传统的分数阶矩估计法相比，由于本发明得到的形状参数α为闭合表达式，不仅能够有效扩大形状参数的估计范围，并且避免了复杂的数值运算，有效地减少了运算时间，提高了估计效率；

实验仿真表明：本发明提出的负一二阶矩估计法能有效估计(0,+∞)范围内的所有形状参数，且参数估计所用的时间最短，减小了运算量，表明本发明能有效提高估计效率。

附图说明

图1是本发明的实现流程图；

图2是本发明中使用的16次观测Pareto分布随机数与理论概率密度函数的拟合曲线图；

图3是用本发明和现有三种估计方法对同一组Pareto分布随机数进行参数估计得到的估计结果与真值的对比曲线图；

图4是用本发明和现有三种估计方法对同一组Pareto分布随机数进行参数估计得到的估计结果相对偏差曲线图；

图5是用本发明和现有三种估计方法对同一组Pareto分布随机数进行参数估计得到的估计结果相对方差曲线图。

具体实施方式：

本发明针对现有对海杂波Pareto分布模型形状参数估计方法的优缺点，提出负一二阶矩估计方法，得到闭合的形状参数估计表达式，通过仿真实验将本发明与一二阶矩估计法、正分数阶矩估计法、负分数阶矩估计法进行对比，证明本发明不仅有效地扩大形状参数的估计范围，并且提高了估计效率。

下面结合附图和具体实施例对本发明作进一步详细描述。

参照图1，本发明的海杂波Pareto分布模型的参数估计范围拓展方法，包括如下步骤：

步骤1，建立海杂波的Pareto分布模型f_N(z)。

(1a)根据海杂波的复合模型理论，得到单次观测的海杂波概率密度函数为：

$f\left(z\right)={\&Integral;}_0^{\mathrm{\&infin;}}p\left(x\right)q\left(z\right|x)dx---\&lt;1\&gt;$

其中，x表示海杂波的结构分量，z表示海杂波的实际观测值，p(x)表示海杂波结构分量的概率密度函数，q(z|x)表示海杂波散斑分量的概率密度函数；

(1b)根据当p(x)服从逆Gamma分布时，海杂波观测值z服从Pareto分布的特性，得到所述p(x)的表达式为：

$p\left(x\right)=\frac{{\mathrm{\&beta;}}^{\mathrm{\&alpha;}}}{\mathrm{\&Gamma;}\left(\mathrm{\&alpha;}\right)}{x}^{-\mathrm{\&alpha;}-1}\exp (-\frac{\mathrm{\&beta;}}{x})---\&lt;2\&gt;$

其中，α表示海杂波模型的形状参数，β表示海杂波模型的尺度参数，α>0，β>0，z≥β，Γ(·)表示Gamma函数；

(1c)设p(x)保持不变，且N次观测后q(z|x)服从参数为N的Gamma分布，得到q(z|x)的表达式为：

$q\left(z\right|x)=\frac{z^{N-1}}{x^N\mathrm{\&Gamma;}\left(N\right)}\exp (-\frac{z}{x})---\&lt;3\&gt;$

其中，N表示观测次数或脉冲积累次数；

(1d)将式<2>和式<3>代入式<1>中，得到N次观测的海杂波Pareto分布模型的概率密度函数为：

$f_N\left(z\right)=\frac{z^{N-1}{\mathrm{\&beta;}}^{\mathrm{\&alpha;}}\mathrm{\&Gamma;}(N+\mathrm{\&alpha;})}{{(\mathrm{\&beta;}+z)}^{N+\mathrm{\&alpha;}}\mathrm{\&Gamma;}\left(N\right)\mathrm{\&Gamma;}\left(\mathrm{\&alpha;}\right)}---\&lt;4\&gt;.$

步骤2，利用海杂波N次观测的Pareto分布概率密度函数，推导出海杂波的实际观测值z的r阶原点矩估计表达式<z^r>。

(2a)记<z^r>为z的r阶原点矩，其计算公式为：

$\&lt;z^r\&gt;={\&Integral;}_0^{\mathrm{\&infin;}}{z}^r{f}_N\left(z\right)dz---\&lt;5\&gt;;$

(2b)将海杂波的Pareto分布模型f_N(z)代入式<5>，得到如下表达式为：

$\&lt;z^r\&gt;={\&Integral;}_0^{\mathrm{\&infin;}}\frac{z^{N+r-1}{\mathrm{\&beta;}}^{\mathrm{\&alpha;}}\mathrm{\&Gamma;}(N+\mathrm{\&alpha;})}{{(\mathrm{\&beta;}+z)}^{N+\mathrm{\&alpha;}}\mathrm{\&Gamma;}\left(N\right)\mathrm{\&Gamma;}\left(\mathrm{\&alpha;}\right)}dz---\&lt;6\&gt;;$

(2c)令得到将z和dz代入式<6>，简化得到z的r阶原点矩<z^r>为：

$\&lt;z^r\&gt;=\frac{{\mathrm{\&beta;}}^r\mathrm{\&Gamma;}(N+\mathrm{\&alpha;})}{\mathrm{\&Gamma;}\left(N\right)\mathrm{\&Gamma;}\left(\mathrm{\&alpha;}\right)}{\&Integral;}_0^{\mathrm{\&infin;}}{\left(y\right)}^{N+r-1}{(1-y)}^{\mathrm{\&alpha;}-r-1}dy---\&lt;7\&gt;;$

(2d)对式<7>进行整理，得到z的r阶原点矩<z^r>的最终表达式为：

$\&lt;z^r\&gt;=\frac{{\mathrm{\&beta;}}^r\mathrm{\&Gamma;}(N+r)\mathrm{\&Gamma;}(\mathrm{\&alpha;}-r)}{\mathrm{\&Gamma;}\left(N\right)\mathrm{\&Gamma;}\left(\mathrm{\&alpha;}\right)}---\&lt;8\&gt;.$

步骤3，将r取值扩大到负数范围，对海杂波模型的形状参数α进行估计。

(3a)为避免β的指数幂对计算效率的影响，分别取r＝-M₁与r＝-M₂，记为z的-M₁阶原点矩，为z的-M₂阶原点矩，对和进行求幂的比值运算，消去β的指数幂，得到如下表达式为：

$\frac{\&lt;z^{-M_1}{\&gt;}^{M_2}}{\&lt;z^{-M_2}{\&gt;}^{M_1}}=\frac{{\mathrm{\&Gamma;}}^{M_2}(N-M_1){\mathrm{\&Gamma;}}^{M_2}(\mathrm{\&alpha;}+M_1){\mathrm{\&Gamma;}}^{M_1}\left(N\right){\mathrm{\&Gamma;}}^{M_1}\left(\mathrm{\&alpha;}\right)}{{\mathrm{\&Gamma;}}^{M_1}(N-M_2){\mathrm{\&Gamma;}}^{M_1}(\mathrm{\&alpha;}+M_2){\mathrm{\&Gamma;}}^{M_2}\left(N\right){\mathrm{\&Gamma;}}^{M_2}\left(\mathrm{\&alpha;}\right)}---\&lt;9\&gt;$

其中，M₁和M₂为正整数，N-M₁>0，N-M₂>0；

(3b)根据Gamma函数的性质，对于任意正整数i和j有:

Γ(i)＝(i-1)(i-2)…(i-j)Γ(i-j) <10>

其中，i>j；

根据式<10>，对式<9>进行化简，得到如下闭合表达式为：

$\frac{\&lt;z^{-M_1}{\&gt;}^{M_2}}{\&lt;z^{-M_2}{\&gt;}^{M_1}}={\left(\frac{(\mathrm{\&alpha;}+M_1-1)(\mathrm{\&alpha;}+M_1-2)...\mathrm{\&alpha;}}{(N-1)(N-2)...(N-M_1)}\right)}^{M_2}\&CenterDot;{\left(\frac{(N-1)(N-2)...(N-M_2)}{(\mathrm{\&alpha;}+M_2-1)(\mathrm{\&alpha;}+M_2-2)...\mathrm{\&alpha;}}\right)}^{M_1}---\&lt;11\&gt;;$

(3c)为简化运算，取M₁＝1、M₂＝2代入式<11>，得到用z的负一阶原点矩和负二阶原点矩估计α的表达式为：

$\frac{\&lt;z^{-1}{\&gt;}^2}{\&lt;z^{-2}\&gt;}={\left(\frac{\mathrm{\&alpha;}}{N-1}\right)}^2\&CenterDot;\frac{(N-1)(N-2)}{(\mathrm{\&alpha;}+1)\mathrm{\&alpha;}}---\&lt;12\&gt;$

其中，<z^-1>为z的负一阶原点矩，<z^-2>为z的负二阶原点矩；

(3d)将式<12>进行整理，得到海杂波形状参数α的最终估计表达式为：

$\mathrm{\&alpha;}=\frac{(N-1)\&lt;z^{-1}{\&gt;}^2}{(N-2)\&lt;z^{-2}\&gt;-(N-1)\&lt;z^{-1}{\&gt;}^2}---\&lt;13\&gt;.$

当观测次数N>2时，可用式<13>估计形状参数在α∈(0,+∞)范围内的Pareto分布参数，完成对海杂波Pareto分布模型的参数估计范围的扩展，并且得到的估计表达式<13>为闭合表达式，计算简便，可以有效提高估计效率。

下面结合具体的仿真测试结果进一步说明本发明的有益效果。

1.仿真条件：

如表1所列：

表1仿真参数

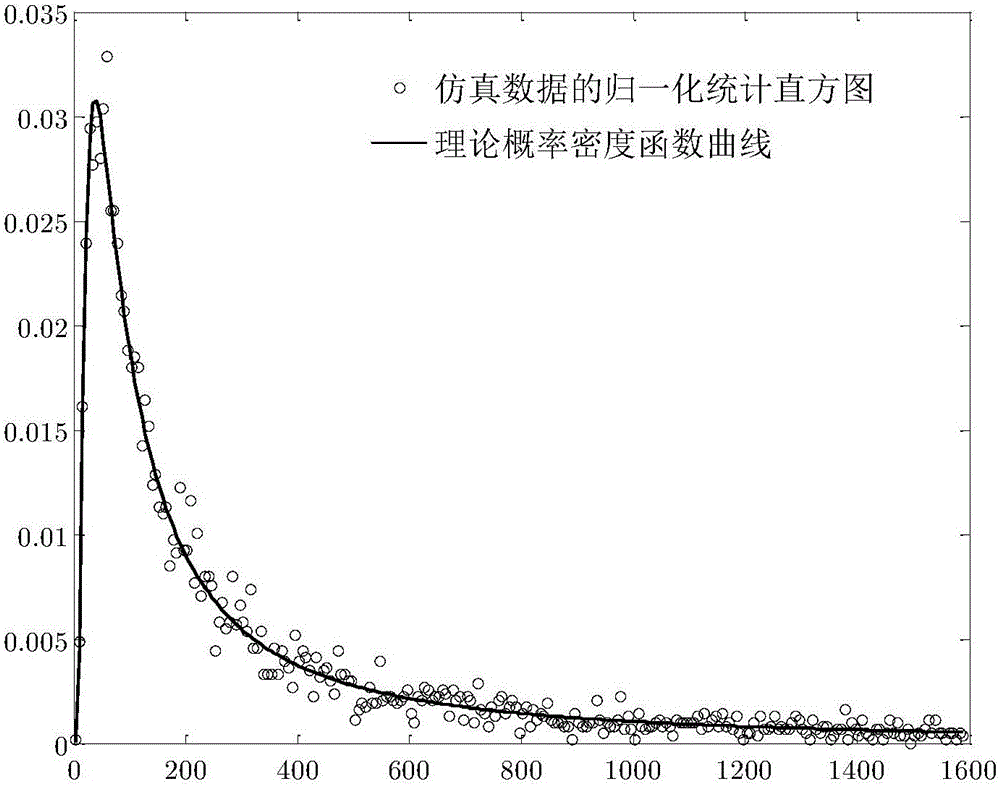
仿真1：在表1的仿真条件下，通过Matlab产生对应参数的Pareto分布随机数作为待估计样本，将产生随机数的统计分布与对应参数的理论概率密度函数进行对比拟合，结果如图2所示。

图2表明本发明使用的仿真数据统计分布与理论概率密度函数具有良好的拟合度，可以模拟真实情况下N次观测时服从Pareto分布的海杂波。

仿真2：在表1的仿真条件下，产生100组海杂波数据样本，分别采用现有的一二阶矩估计法、正分数阶矩估计法、负分数阶矩估计法和本发明对形状参数进行估计。

具体步骤如下：

1)采用一二阶矩估计法对海杂波形状参数进行估计，估计结果记为α₁；

1a)分别取r＝1，r＝2，记<z>为z的一阶原点阶矩，<z²>为z的二阶原点阶矩，对<z>和〈z²〉进行求幂的比值运算，消去β的指数幂，得到如下的表达式为：

$\frac{\&lt;z{\&gt;}^2}{\&lt;z^2\&gt;}=\frac{{\mathrm{\&Gamma;}}^2(N+1){\mathrm{\&Gamma;}}^2({\mathrm{\&alpha;}}_1-1)\mathrm{\&Gamma;}\left(N\right)\mathrm{\&Gamma;}\left({\mathrm{\&alpha;}}_1\right)}{\mathrm{\&Gamma;}(N+2)\mathrm{\&Gamma;}({\mathrm{\&alpha;}}_1-2){\mathrm{\&Gamma;}}^2\left(N\right){\mathrm{\&Gamma;}}^2\left({\mathrm{\&alpha;}}_1\right)}---\&lt;14\&gt;$

其中，α₁-2>0；

1b)根据Gamma函数的性质，将式<14>进行化简，得到如下的闭合表达式为：

${\left(\frac{N}{{\mathrm{\&alpha;}}_1-1}\right)}^2\&CenterDot;\frac{({\mathrm{\&alpha;}}_1-1)({\mathrm{\&alpha;}}_1-2)}{(N+1)N}=\frac{\&lt;z{\&gt;}^2}{\&lt;z^2\&gt;}---\&lt;15\&gt;;$

1c)将式<15>进行整理，得到α₁的估计表达式为：

${\mathrm{\&alpha;}}_1=\frac{\&lt;z{\&gt;}^2}{\frac{N}{N+1}\&lt;z^2\&gt;-\&lt;z{\&gt;}^2}+2---\&lt;16\&gt;;$

2)采用正分数阶矩估计法对海杂波形状参数进行估计，估计结果记为α₂；

2a)分别取记为z的阶原点阶矩，为z的阶原点阶矩，对和进行求幂的比值运算，消去β的指数幂，得到如下的表达式为：

$\frac{\&lt;z^{\frac{1}{2}}{\&gt;}^{\frac{1}{4}}}{\&lt;z^{\frac{1}{4}}{\&gt;}^{\frac{1}{2}}}=\frac{{\mathrm{\&Gamma;}}^{\frac{1}{4}}(N+\frac{1}{2}){\mathrm{\&Gamma;}}^{\frac{1}{4}}({\mathrm{\&alpha;}}_2-\frac{1}{2}){\mathrm{\&Gamma;}}^{\frac{1}{2}}\left(N\right){\mathrm{\&Gamma;}}^{\frac{1}{2}}\left({\mathrm{\&alpha;}}_2\right)}{{\mathrm{\&Gamma;}}^{\frac{1}{2}}(N+\frac{1}{4}){\mathrm{\&Gamma;}}^{\frac{1}{2}}({\mathrm{\&alpha;}}_2-\frac{1}{4}){\mathrm{\&Gamma;}}^{\frac{1}{4}}\left(N\right){\mathrm{\&Gamma;}}^{\frac{1}{4}}\left({\mathrm{\&alpha;}}_2\right)}---\&lt;17\&gt;$

其中，

2b)采用拉格朗日插值法对式<17>进行运算，得到α₂的估计结果；

3)采用负分数阶矩估计法对海杂波形状参数进行估计，估计结果记为α₃；

3a)分别取记为z的阶原点阶矩，为z的阶原点阶矩，对和进行求幂的比值运算，消去β的指数幂，得到如下的表达式为：

$\frac{\&lt;Z^{-\frac{1}{4}}{\&gt;}^2}{\&lt;Z^{-\frac{1}{2}}\&gt;}=\frac{{\mathrm{\&Gamma;}}^2(N-\frac{1}{4}){\mathrm{\&Gamma;}}^2(\mathrm{\&alpha;}+\frac{1}{4})}{\mathrm{\&Gamma;}(N-\frac{1}{2})\mathrm{\&Gamma;}(\mathrm{\&alpha;}+\frac{1}{2})\mathrm{\&Gamma;}\left(N\right)\mathrm{\&Gamma;}\left(\mathrm{\&alpha;}\right)}---\&lt;18\&gt;$

其中，

3b)采用拉格朗日插值法对式<18>进行运算，得到α₃的估计结果；

4)采用本发明对海杂波形状参数进行估计，结果记为α₄；

5)结合仿真结果，分析α₁、α₂、α₃和α₄的估计范围，比较四种估计方法的估计值，如图3所示。从图3可得出以下结果：

当用现有一二阶矩估计法在形状参数小于2时，估计值与真值误差较大，根据步骤1a)，采用一二阶矩估计法对形状参数进行估计，应满足α₁-2>0，可用式<16>估计形状参数在α₁∈(2,+∞)范围内的Pareto分布参数，当形状参数真值小于等于2时，此方法不适用；

当用现有的正分数阶矩估计法在形状参数小于阶数时，估计值与真值也有较大的误差，根据步骤2a)，采用正分数阶矩估计法对形状参数进行估计，应满足正分数阶矩估计法可以估计形状参数在范围内的Pareto分布参数，当形状参数真值小于等于阶数时，此方法不适用；

当用本发明和负分数阶矩估计法时，其估计值与真值始终吻合很好，表明本发明可以估计形状参数在α₄∈(0,+∞)范围内的Pareto分布参数，有效扩展了估计范围。

仿真3：在表1的仿真条件下，对仿真1产生的100组海杂波数据样本，分别采用现有的一二阶矩估计法、正分数阶矩估计法、负分数阶矩估计法和本发明对形状参数进行估计，比较四种方法估计值的相对偏差结果如图4所示。

图4表明：四种方法估计结果的相对偏差随着形状参数的增大趋于相等，但当形状参数较小时，与一二阶矩估计法和正分数阶矩估计法相比，本发明得到的估计结果具有较小的相对偏差。

仿真4：在表1的仿真条件下，对仿真1产生的100组海杂波数据样本，分别采用现有的一二阶矩估计法、正分数阶矩估计法、负分数阶矩估计法和本发明对形状参数进行估计，比较四种方法估计值的相对方差结果如图5所示。

图5表明：四种方法估计结果的相对方差随着形状参数的增大趋于相等，但当形状参数较小时，与一二阶矩估计法和正分数阶矩估计法相比，本发明得到的估计结果具有较小的相对方差。

仿真5：在表1的仿真条件下，对仿真1产生的100组海杂波数据样本，在同一台计算机上对每一组海杂波仿真数据分别采用现有的一二阶矩估计法、正分数阶矩估计法、负分数阶矩估计法和本发明进行参数估计实验，记录采用每一种估计方法时计算机的运行时间，取平均估计时间，结果如表2所示：

表2不同r值时的平均估计时间

表2表明：与正分数阶矩估计法和负分数阶矩估计法相比，一二阶矩估计法与本发明运算时间更短；根据步骤1c)和步骤4)，一二阶矩估计法与本发明的估计结果都得到了闭合的估计表达式；根据步骤2c)和步骤3b)，正分数阶矩估计法和负分数阶矩估计法在计算估计结果时，需要进行复杂的数值运算，运算效率低下。表明本发明具有实用性，能够有效提高估计效率。