基于改进了适用范围的卡尔曼滤波的静态PET图像重建方法与流程

本发明涉及正电子发射断层成像技术领域，具体涉及一种基于改进了适用范围的卡尔曼滤波的静态pet图像重建方法。

背景技术：

正电子发射断层成像(positronemissiontomography，pet)是一种基于核物理学、分子生物学的医学影像技术，与ct成像不同，pet作为一种功能性成像技术，能够检测生物体内新陈代谢的情况，并在分子水平上反映生物体的生理或病理变化，能为早期疾病的检测与预防提供有效依据，现已被广泛应用于肿瘤、心脏疾病、神经和精神系统疾病的诊断及药物筛选与开发，具有巨大的应用前景。

在进行pet扫描时首先使用医用回旋加速器产生正电子发射核素，然后将标记了放射性同位核素的示踪剂注入生物体内，通过血液循环，示踪剂会在生物体各组织器官中形成一定的浓度分布。放射性同位核素极不稳定，会发生衰变。在衰变过程中，放射性同位核素会产生正电子并与组织器官周围环境中的自由电子发生湮灭反应，产生一对几乎方向相反、能量相等的伽玛光子。pet扫描能够捕捉这些光子进而生成投影数据。基于这些投影数据和重构算法，可重建出组织器官内放射性物质的浓度分布。但由于经由pet扫描采集到的投影数据中包含了大量的噪声信息，这将会影响pet图像重建的质量，所以pet图像的重建算法是现今研究的一大热点。

目前，pet图像重建方法大致可分为两类：解析法、迭代法。前一类主要以滤波反投影法为代表，计算速度快，代价小，但并不能很好地抑制噪声，以致伪影严重，重建图像质量不高。因此，出现了以较为典型的ml-em为代表的统计迭代法。统计迭代法对不完全数据适应性好，获得的重建图像比解析法更加清晰，很快成为pet重建算法研究的焦点。状态空间观测模型的引入，使得基于卡尔曼滤波、h∞滤波等估计算法重建pet图像成为可能。尽管如此，由于未使用投影数据的统计特性、验证惯性条件困难，基于h∞滤波的pet重构结果具有重构结果保守、计算量大等问题；由于在处理器中无法存储的原因，基于标准卡尔曼滤波的重构方法无法适用于对初始放射性物质浓度估计完全没把握(即放射性物质浓度的初始估计误差协方差阵无限大)的情况。

技术实现要素：

为了克服现有pet图像重建方法的无法适用于对初始放射性物质浓度估计完全没把握的情况、适用范围较窄的不足，本发明提供了一种有效扩大适用范围的基于改进了适用范围的卡尔曼滤波的静态pet图像重建方法，该发明首先将原本无法存储的趋于无穷大的放射性物质空间浓度的初始预估误差协方差阵以其逆的形式存储为零矩阵，然后通过离线、迭代计算预估误差协方差阵的逆矩阵，进而基于逆矩阵计算滤波增益，最终保证了重构过程的顺利进行。

为了解决上述技术问题本发明提供如下的技术方案：

一种基于改进了适用范围的卡尔曼滤波的静态pet图像重建方法，包括如下步骤：

(1)通过数据采集及校正，得到系统的观测数据，建立pet系统的状态空间模型：

其中，t表示时间；xt为需要重建的对象在t时刻的放射性物质的空间浓度分布；yt为t时刻的观测值，是经过噪声矫正后得到的正弦图数据；ht表示人体内放射性物质的空间浓度与正弦图数据之间投影关系的投影矩阵；vt是t时刻数据采集并经噪声矫正后残留的噪声，vt服从均值为0，方差为r的正态分布；

(2)根据下列方程得到基于改进了适用范围的卡尔曼滤波的重建图像：

其中，为放射性物质的空间浓度的初始估计值，m为初始放射性物质的空间浓度的预估误差协方差阵的逆矩阵，it为t时刻放射性物质的空间浓度的预估误差协方差阵的逆矩阵，kt是t时刻的滤波增益矩阵，为t时刻的放射性物质的空间浓度的估计值，迭代从初始值i0出发，结合观测值yt，经过t次迭代，得到最终的放射性物质的空间浓度分布的估计值

进一步，所述步骤(2)中，重建迭代过程如下：

2.1)首先设定放射性物质的空间浓度分布的初始值和初始放射性物质的空间浓度预估误差协方差阵的逆矩阵i0；

2.2)利用方程(1.4)计算t时刻的放射性物质的空间浓度的预估误差协方差阵的逆矩阵it；

2.3)利用t时刻的放射性物质的空间浓度的预估协方差阵的逆矩阵it根据方程(1.3)计算t时刻的滤波增益矩阵kt；

2.4)利用t-1时刻放射性物质的空间浓度估计值根据方程(1.2)计算t时刻的放射性物质的空间浓度估计值

2.5)重复步骤2.2)，2.3)，2.4)直至获得满足要求的最终重建结果

2.6)根据步骤2.5)得到最终的放射性物质的空间浓度分布的估计值

本发明的技术构思为：基于对pet系统使用标准卡尔曼滤波方法成像原理的分析，发现该重构方法无法适用于对初始的放射性物质浓度分布完全没把握(即初始放射性物质浓度分布的估计误差协方差阵无穷大)的情况。该发明首先将原本无法存储的趋于无穷大的放射性物质空间浓度的初始预估误差协方差阵以其逆的形式存储为零矩阵，然后通过离线、迭代计算预估误差协方差阵的逆矩阵，进而基于逆矩阵计算滤波增益，最终保证了重构过程的顺利进行。

从上述技术方案可以看出，本发明的有益效果主要表现在：引入放射性物质浓度预估误差协方差阵的逆矩阵能将原本无穷大的图像预估误差协方差阵转化为零矩阵进行存储，因而扩大了基于卡尔曼滤波的静态pet图像重构方法的适用范围。

附图说明

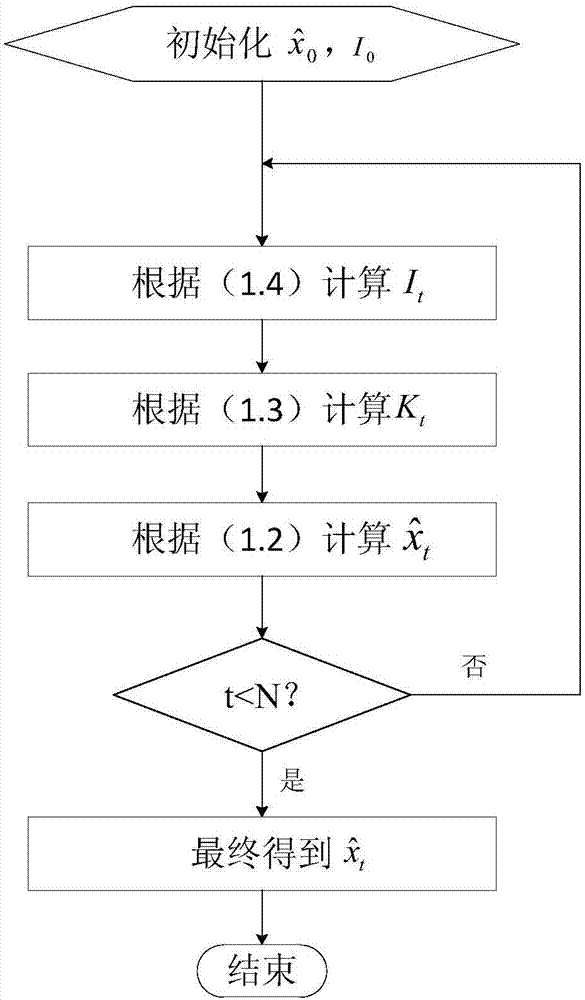
图1为本发明pet图像重建方法的步骤流程示意图。

具体实施方式

为了更为具体地描述本发明，下面结合附图及具体实施方式对本发明的静态pet浓度重建方法进行详细说明。

如图1所示，一种基于改进了适用范围的卡尔曼滤波的静态pet图像重建方法，包括如下步骤：

⑴通过数据采集及校正，得到系统的观测数据，建立pet系统的状态空间模型；：

其中，t表示时间；xt为需要重建的对象t时刻的放射性物质的空间浓度分布；yt为t时刻的观测值，是经过噪声矫正后得到的正弦图数据；ht表示人体内放射性物质的空间浓度与正弦图数据之间投影关系的投影矩阵；vt是t时刻数据采集并经噪声矫正后残留的噪声，vt服从均值为0，方差为r的正态分布。

⑵根据下列方程得到基于改进了适用范围的卡尔曼滤波的静态pet重建图像：

其中，为放射性物质的空间浓度的初始估计值，m为初始放射性物质的空间浓度的预估误差协方差阵的逆矩阵，it为t时刻放射性物质的空间浓度的预估误差协方差阵的逆矩阵，kt是t时刻的滤波增益矩阵，为t时刻的放射性物质的空间浓度的估计值，迭代从初始值i0出发，结合观测值yt，经过t次迭代，得到最终的放射性物质的空间浓度分布的估计值

如图1所示，基于改进了适用范围的卡尔曼滤波的图像重建迭代过程如下：

2.1)首先设定放射性物质的空间浓度分布的初始值和初始放射性物质的空间浓度预估误差协方差阵的逆矩阵i0；

2.2)利用方程(1.4)计算t时刻的放射性物质的空间浓度的预估误差协方差阵的逆矩阵it；

2.3)利用t时刻的放射性物质的空间浓度的预估协方差阵的逆矩阵it根据方程(1.3)计算t时刻的滤波增益矩阵kt；

2.4)利用t-1时刻放射性物质的空间浓度估计值根据方程(1.2)计算t时刻的放射性物质的空间浓度估计值

2.5)重复步骤2.2)，2.3)，2.4)直至获得满足要求的最终重建结果

2.6)根据步骤2.5)得到最终的放射性物质的空间浓度分布的估计值