基于稀疏共同空间模式的癫痫EEG自动检测的通道优化方法与流程

本发明涉及信号处理与神经工程领域，特别是一种癫痫脑电信号检测与识别方法。

背景技术：

全世界大约5千多万人患有癫痫。癫痫是由于大脑神经元异常放电，波及某些大脑功能区，造成大脑神经紊乱的一种疾病。脑电图(eeg)是记录大脑放电行为的一种有效方式，也是临床检测和诊断癫痫发作的一种方式。基于eeg的癫痫的自动检测不仅对临床分析癫痫等神经疾病具有重要价值，而且是预报癫痫发作的一种有效途径。专利“一种面向癫痫脑电信号迁移环境的自适应识别方法”，专利“面向癫痫脑电信号的特征提取与自动识别方法”，“一种癫痫发作预警系统”。在癫痫eeg检测与识别中都需要处理多通道的数据。开发一种利用少量电极(通道)检测癫痫eeg不仅可降低检测时间，而且可以降低系统功耗。本发明公开了一种基于稀疏共同空间模式的癫痫eeg自动检测的通道优化方法。

技术实现要素：

本发明的目的是提供一种癫痫eeg自动检测的通道优化方法。

为了解决上述技术问题，本发明提供了一种癫痫eeg自动检测的通道优化方法，包括：生成空域滤波器，且通过空域滤波器对电极产生的数据通道进行优化。

进一步，生成空域滤波器的方法包括：

将空域滤波器的稀疏度作为优化目标，去除不相关或是受噪声干扰较大的数据通道；其中

所述稀疏度由其系数向量的l0范数衡量。

进一步，所述生成空域滤波器的方法还包括：

构建初始模型，即

其中，n为eeg信号通道数，c1与c2分别表示两类信号的协方差矩阵；τ是一个预先设置的阈值，用于调节不同类别信号的平均功率比值；

并且tr(w^tcw)＝tr(cww^t)(6)

引入矩阵w＝ww^t，则公式(5)改写为

w＝ww^t(7)

其中，||w||0,1定义为

上式中，ia(x)为示性函数；

由于第二个约束条件w＝ww^t，并且w是一个半正定矩阵，进一步将约束条件w＝ww^t松弛为半正定约束条件w≥0；以及

利用l1范数代替目标函数中的l0范数，从而获得以下模型：

w≥0

tr(w)＝1(10)

其中

上式中，wi,:表示w的第i行；

求解公式(10)可以获得空域滤波器系数向量w1；以及

将公式(10)中的第一个约束条件改为则可获得另一空域滤波器系数向量w2。

进一步，所述阈值τ与算法分类精度相关；即

在使用时，首先获得或其中wcsp表示预先获得的空域滤波器系数；

将公式(10)中的门限值τ记为τsdp-csp，且将门限值设置为τsdp-csp＝ρ·τcsp，ρ∈(0,1)。

进一步，数据通道进行优化的方法包括：

将滤波器系数向量w1或滤波器系数向量w2内幅度值小于所有元素中最大幅度0.1％的系数置为零；即

当滤波器系数向量w1与滤波器系数向量w2对应元素都已置零时，该元素所对应的通道被彻底舍弃。

本发明的有益效果是，本发明的癫痫eeg自动检测的通道优化方法通过选取少量的有效信号采集通道，并获取各个通道对应的空域滤波器，一旦确定所选通道，后续则只需要利用数量较少的有效通道上的eeg信号完成分类任务。

附图说明

下面结合附图和实施例对本发明进一步说明。

图1是本发明的通道选择示意图；

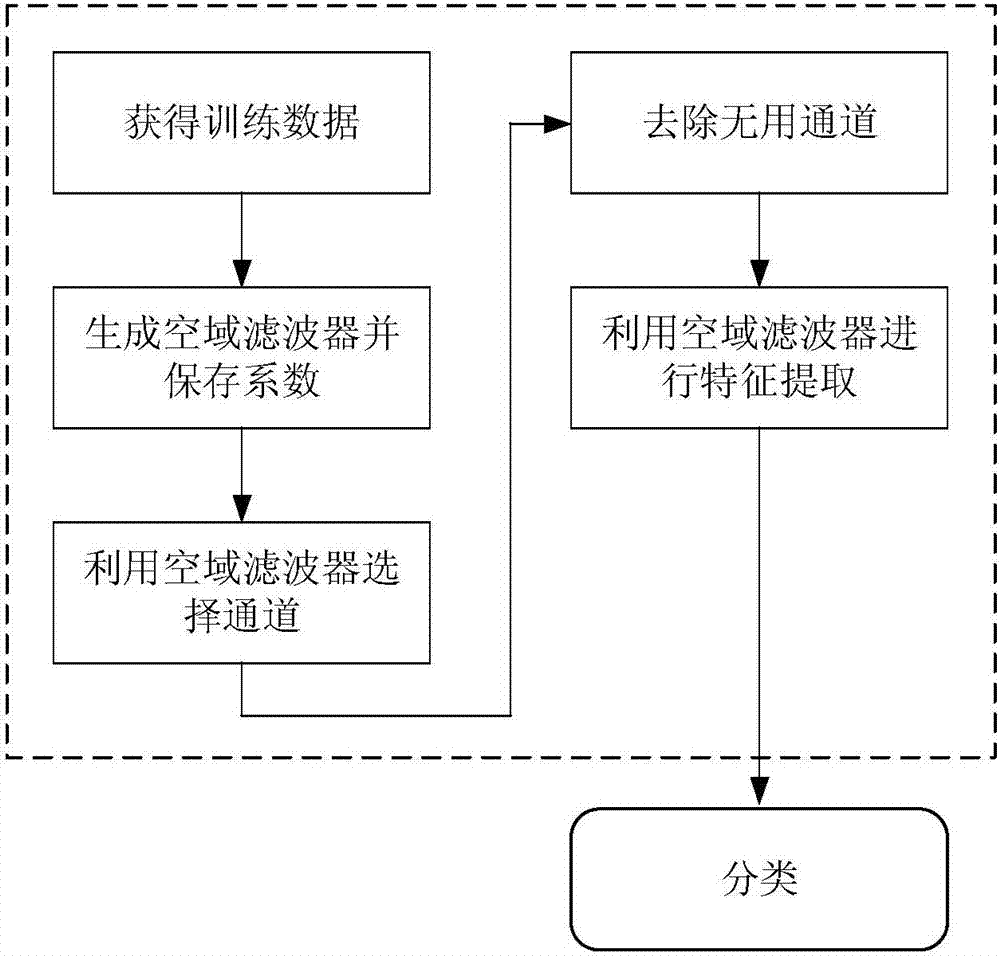
图2是本发明的通道优化方法的流程图。

具体实施方式

现在结合附图对本发明作进一步详细的说明。这些附图均为简化的示意图，仅以示意方式说明本发明的基本结构，因此其仅显示与本发明有关的构成。

传统的csp算法寻找一组使得两类信号平均功率差距最大的空域滤波器，可以表述为

其中，n为eeg信号通道数，c1与c2分别表示两类信号的协方差矩阵

其中，x为第一类或第二类eeg信号。上式中的协方差矩阵具有半正定特性。

w^tc1w＝λ¹

w^tc2w＝λ²

λ¹+λ²＝i(3)

其中，w由协方差矩阵c1与c2的广义特征向量wj组成，即w＝[w1,w2,…..,wj]，用于同时对角化c1与c2，λⁱ＝diag(λ1ⁱ,…λjⁱ)为对角矩阵，包含ci的特征值λjⁱ(i＝1,2，j＝1,2,......,n)。利用公式(3)，csp问题可以转化为以下优化问题

根据公式(3)中λ¹+λ²＝i可知c1与c2中wj对应的特征值λj¹+λj²＝1，此外由于c1和c2均为半正定矩阵，所以λjⁱ≥0。因此，λj¹越大，λj²就越小，同时λj¹/λj²也随之增大，所以最大特征值λj¹对应的特征向量就是公式(1)的解。

在传统csp算法的基础上，本发明提供了一种癫痫eeg自动检测的通道优化方法，包括：

生成空域滤波器，且通过空域滤波器对电极产生的数据通道进行优化。

具体的，生成空域滤波器的方法包括：

将空域滤波器的稀疏度作为优化目标，去除不相关或是受噪声干扰较大的数据通道；其中

所述稀疏度由其系数向量的l0范数衡量。

所述生成空域滤波器的方法还包括：

构建初始模型，即

其中，n为eeg信号通道数，c1与c2分别表示两类信号的协方差矩阵；τ是一个预先设置的阈值，用于调节不同类别信号的平均功率比值；

并且tr(w^tcw)＝tr(cww^t)(6)

引入矩阵w＝ww^t，则公式(5)改写为

w＝ww^t(7)

其中，||w||0,1定义为

上式中，ia(x)为示性函数；

由于第二个约束条件w＝ww^t，公式(7)仍然为一个非凸优化问题，并且w是一个半正定矩阵，进一步将约束条件w＝ww^t松弛为半正定约束条件w≥0；以及利用l1范数代替目标函数中的l0范数，从而获得以下模型：

w≥0

tr(w)＝1(10)

其中

上式中，wi,:表示w的第i行；

公式(10)中附加了约束条件tr(w)＝1，用于消除w由于缩放所带来的不确定性；公式(10)是一个半定规划(semi-definiteprogramming，sdp)问题，因此将其本优化方法所涉及的算法简写为sdp-csp；求解公式(10)可以获得空域滤波器系数向量w1；若将公式(10)中的第一个约束条件改为则可获得另一空域滤波器系数向量w2。

进一步，所述阈值τ与算法分类精度相关；即

在使用时，首先获得或其中wcsp表示预先获得的空域滤波器系数；为了清晰起见，将公式(10)中的门限值τ记为τsdp-csp，且将门限值设置为τsdp-csp＝ρ·τcsp，ρ∈(0,1)。

如图2所示，数据通道进行优化的方法包括：

由于l1范数的作用，w1和w2中包含许多幅度极小的元素，将这些滤波器系数置零，从而可以获得两组稀疏滤波器；将滤波器系数向量w1或滤波器系数向量w2内幅度值小于所有元素中最大幅度0.1％的系数置为零；即当滤波器系数向量w1与滤波器系数向量w2对应元素都已置零时，该元素所对应的通道被彻底舍弃。

如图2所示，利用训练数据，选取少量的有效信号采集通道，并获取各个通道对应的空域滤波器，一旦确定所选通道，后续则只需要利用数量较少的有效通道上的eeg信号完成分类任务。

以上述依据本发明的理想实施例为启示，通过上述的说明内容，相关工作人员完全可以在不偏离本项发明技术思想的范围内，进行多样的变更以及修改。本项发明的技术性范围并不局限于说明书上的内容，必须要根据权利要求范围来确定其技术性范围。