人机共驾冲突控制方法、装置、存储介质及电子设备与流程
1.本公开涉及自动驾驶技术领域,具体涉及一种人机共驾冲突控制方法、人机共驾冲突控制装置、存储介质及电子设备。
背景技术:
2.由于自动驾驶系统与驾驶员都是智能体,均会根据自身对场景的理解做出判断和决策,因此除了在共驾系统控制层人机预瞄行为差异所致的人机转向冲突外,人机冲突的另一个主要成因是因为人机决策层分歧,即驾驶员与自动驾驶系统规划的目标轨迹存在差异,进而引发转向力矩冲突。
3.然而,在人机交互机理建模中,驾驶员决策目标难以直接测得,尤其是针对车辆极限工况下(例如人机协同式紧急避让)的人机交互的建模过程中,人机交互行为难以直接应用线性动力学模型描述。
4.许多非线性方法,如非线性预测方法、局部线性化方法、以及分段仿射方法均被应用于为处理车辆极限工况下的模型失配问题,然而,非线性预测方法往往由于其高运算复杂度而导致算法实时性能不佳。局部线性化或分段仿射方法虽然能够保证算法的实时性,但这些方法难以避免地导致控制策略在不同线性化区间之内来回切换,使得人机交互结果产生不平滑现象,甚至出现在线性分段点附近来回切换的滑模现象。
5.需要说明的是,在上述背景技术部分公开的信息仅用于加强对本公开的背景的理解,因此可以包括不构成对本领域普通技术人员已知的现有技术的信息。
技术实现要素:
6.本公开的目的在于提供一种人机共驾冲突控制方法,旨在对人机决策分歧与人机转向力矩交互间的映射关系进行描述,以提高车辆控制精度。
7.本公开的其他特性和优点将通过下面的详细描述变得显然,或部分地通过本公开的实践而习得。
8.根据本公开实施例的一方面,提供了一种人机共驾冲突控制方法,包括:基于驾驶员的确定性转向力矩和驾驶员的随机性转向力矩建立人机交互行为对应的人机路径跟踪控制博弈模型;求解所述人机路径跟踪控制博弈模型得到人机力矩冲突信息;根据所述人机力矩冲突信息确定共享控制策略,以根据所述共享控制策略进行车辆控制。
9.根据本公开的一些实施例,基于前述方案,在所述人机路径跟踪控制博弈模型为闭环博弈模型时,基于驾驶员的确定性转向力矩和驾驶员的随机性转向力矩建立人机交互行为对应的人机路径跟踪控制博弈模型,包括:基于所述驾驶员的确定性转向力矩和驾驶员的随机性转向力矩建立人机共驾车辆动力学系统在闭环信息模式下的第一离散状态更新方程;通过人机预瞄动态过程对所述第一离散状态更新方程进行增广,得到包含人机预瞄状态的路径跟踪增广系统;基于所述路径跟踪增广系统构造驾驶员轨迹代价函数和驾驶系统轨迹代价函数,以得到所述人机路径跟踪控制博弈模型。
10.根据本公开的一些实施例,基于前述方案,在所述人机路径跟踪控制博弈模型为开环博弈模型时,所述基于驾驶员的确定性转向力矩和驾驶员的随机性转向力矩建立人机交互行为对应的人机路径跟踪控制博弈模型,包括:基于所述驾驶员的确定性转向力矩和驾驶员的随机性转向力矩建立人机共驾车辆动力学系统在开环信息模式下的第二离散状态更新方程;根据所述第二离散状态更新方程确定预测时域内的预测输出向量,并确定驾驶员参考轨迹向量和驾驶系统参考轨迹向量;利用所述预测输出向量、所述驾驶员参考轨迹向量和驾驶系统参考轨迹向量分别构造驾驶员轨迹代价函数和驾驶系统轨迹代价函数,以得到所述人机路径跟踪控制博弈模型。
11.根据本公开的一些实施例,基于前述方案,所述求解所述人机路径跟踪控制博弈模型得到人机力矩冲突信息,包括:采用随机动态规划算法确定纳什均衡条件下的驾驶员和驾驶系统分别对应的转向控制值函数的递归关系;基于所述第一离散状态更新方程和所述递归关系计算驾驶员和驾驶系统分别对应的闭环纳什均衡解作为所述人机力矩冲突信息。
12.根据本公开的一些实施例,基于前述方案,所述求解所述人机路径跟踪控制博弈模型得到人机力矩冲突信息,包括:采用随机动态规划算法确定斯塔克博格均衡条件下的驾驶员和驾驶系统分别对应的转向控制值函数的递归关系;根据驾驶系统对应的转向控制值函数的递归关系确定驾驶员反应函数;基于所述第一离散状态更新方程、所述驾驶员反应函数以及驾驶系统对应的转向控制值函数的递归关系计算驾驶系统对应的开环斯塔克博格均衡解;根据所述驾驶系统对应的开环斯塔克博格均衡解计算驾驶员对应的开环斯塔克博格均衡解,以作为所述人机力矩冲突信息。
13.根据本公开的一些实施例,基于前述方案,所述求解所述人机路径跟踪控制博弈模型得到人机力矩冲突信息,包括:求解所述人机路径跟踪控制博弈模型对应的模型闭式解,以根据所述模型闭式解得到人机转向控制与目标轨迹间的关系表达式;采用凸迭代算法求解所述关系表达式得到驾驶员和驾驶系统分别对应的开环纳什均衡解作为所述人机力矩冲突信息。
14.根据本公开的一些实施例,基于前述方案,所述求解所述人机路径跟踪控制博弈模型得到人机力矩冲突信息,包括:将所述驾驶系统轨迹代价函数转换为考虑驾驶员反应函数的驾驶系统轨迹优化函数;求解所述驾驶系统轨迹优化函数得到驾驶系统对应的开环斯塔克博格均衡解;基于所述开环斯塔克博格均衡解和驾驶员轨迹代价函数计算驾驶员对应的开环斯塔克博格均衡解,以作为所述人机力矩冲突信息。
15.根据本公开实施例的第二方面,提供了一种人机共驾冲突控制装置,包括:建模模块,用于基于驾驶员的确定性转向力矩和驾驶员的随机性转向力矩建立人机交互行为对应的人机路径跟踪控制博弈模型;求解模块,用于求解所述人机路径跟踪控制博弈模型得到人机力矩冲突信息;运用模块,用于根据所述人机力矩冲突信息确定共享控制策略,以根据所述共享控制策略进行车辆控制。
16.根据本公开实施例的第三方面,提供了一种计算机可读存储介质,其上存储有计算机程序,所述程序被处理器执行时实现如上述实施例中的人机共驾冲突控制方法。
17.根据本公开实施例的第四方面,提供了一种电子设备,其特征在于,包括:一个或多个处理器;存储装置,用于存储一个或多个程序,当所述一个或多个程序被所述一个或多
个处理器执行时,使得所述一个或多个处理器实现如上述实施例中的人机共驾冲突控制方法。
18.本公开示例性实施例可以具有以下部分或全部有益效果:
19.在本公开的一些实施例所提供的技术方案中,本公开基于驾驶员的确定性转向力矩和驾驶员的随机性转向力矩建立人机交互行为对应的人机路径跟踪控制博弈模型,并对人机路径跟踪控制博弈模型进行求解,以得到人机力矩冲突信息用于车辆控制,一方面能够对将驾驶员的不确定行为纳入人机路径跟踪控制,使其更符合实际场景需求,控制效果更加精准;另一方面,求解博弈模型得到的人机力矩冲突信息是对人机共驾模型中决策分歧到控制冲突的人机交互行为的精确描述,能够克服共驾系统存在的人机决策混淆问题,进而为共享控制策略设计提供理论依据,进一步优化车辆控制的结果。
20.应当理解的是,以上的一般描述和后文的细节描述仅是示例性和解释性的,并不能限制本公开。
附图说明
21.此处的附图被并入说明书中并构成本说明书的一部分,示出了符合本公开的实施例,并与说明书一起用于解释本公开的原理。显而易见地,下面描述中的附图仅仅是本公开的一些实施例,对于本领域普通技术人员来讲,在不付出创造性劳动的前提下,还可以根据这些附图获得其他的附图。在附图中:
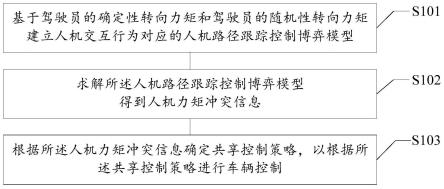
22.图1示意性示出本公开示例性实施例中一种人机共驾冲突控制方法的流程示意图;
23.图2示意性示出本公开示例性实施例中一种人机共驾系统的转向交互的原理示意图;
24.图3示意性示出本公开示例性实施例中一种人机共驾系统的非合作型博弈的原理示意图;
25.图4示意性示出本公开示例性实施例中一种人机共驾系统的闭环动态博弈原理图;
26.图5示意性示出本公开示例性实施例中一种人机共驾系统的开环动态博弈的原理示意图;
27.图6示意性示出本公开示例性实施例中一种构建闭环人机路径跟踪控制博弈模型方法的流程示意图;
28.图7示意性示出本公开示例性实施例中一种多点预瞄模式的原理示意图;
29.图8示意性示出本公开示例性实施例中一种构建开环人机路径跟踪控制博弈模型方法的流程示意图;
30.图9示意性示出本公开示例性实施例中一种求解闭环人机路径跟踪控制博弈模型方法的流程示意图;
31.图10示意性示出本公开示例性实施例中另一种求解闭环人机路径跟踪控制博弈模型方法的流程示意图;
32.图11示意性示出本公开示例性实施例中另一种求解开环人机路径跟踪控制博弈模型方法的流程示意图;
33.图12示意性示出本公开示例性实施例中另一种求解开环人机路径跟踪控制博弈模型方法的流程示意图;
34.图13示意性示出本公开示例性实施例中一种人机共驾冲突控制装置的组成示意图;
35.图14示意性示出本公开示例性实施例中一种计算机可读存储介质的示意图;
36.图15示意性示出本公开示例性实施例中一种电子设备的计算机系统的结构示意图。
具体实施方式
37.现在将参考附图更全面地描述示例实施方式。然而,示例实施方式能够以多种形式实施,且不应被理解为限于在此阐述的范例;相反,提供这些实施方式使得本公开将更加全面和完整,并将示例实施方式的构思全面地传达给本领域的技术人员。
38.此外,所描述的特征、结构或特性可以以任何合适的方式结合在一个或更多实施例中。在下面的描述中,提供许多具体细节从而给出对本公开的实施例的充分理解。然而,本领域技术人员将意识到,可以实践本公开的技术方案而没有特定细节中的一个或更多,或者可以采用其它的方法、组元、装置、步骤等。在其它情况下,不详细示出或描述公知方法、装置、实现或者操作以避免模糊本公开的各方面。
39.附图中所示的方框图仅仅是功能实体,不一定必须与物理上独立的实体相对应。即,可以采用软件形式来实现这些功能实体,或在一个或多个硬件模块或集成电路中实现这些功能实体,或在不同网络和/或处理器装置和/或微控制器装置中实现这些功能实体。
40.附图中所示的流程图仅是示例性说明,不是必须包括所有的内容和操作/步骤,也不是必须按所描述的顺序执行。例如,有的操作/步骤还可以分解,而有的操作/步骤可以合并或部分合并,因此实际执行的顺序有可能根据实际情况改变。
41.在人机双智能体系统中,驾驶员和自动驾驶系统会同时操纵执行器并改变车辆状态以达成各自的目标,而这种输入冗余难免会造成人机冲突交互的产生,严重影响车辆的安全性、舒适性、动力性以及燃油经济性等。
42.博弈理论是一种描述和理解多智能体系统中双方交互冲突的有效手段,为人机交互的量化建模、人机冲突的消解以及驾驶员真实意图的推断提供了有效的理论方法。
43.对于人机共驾型轨迹跟踪控制问题,由于自动驾驶系统与驾驶员都是智能体,均会根据自身对场景的理解做出判断和决策,因此除了在共驾系统控制层人机预瞄行为差异所致的人机转向冲突外,人机冲突的另一个主要成因是因为人机决策层分歧,即驾驶员与自动驾驶系统规划的目标轨迹存在差异,进而引发转向力矩冲突。
44.但一方面,在人机交互机理建模中,尤其是针对车辆极限工况下(如人机协同式紧急避让)的人机交互的建模过程中,人机交互行为难以直接应用线性动力学模型描述,而许多非线性方法如非线性预测方法、局部线性化方法、以及分段仿射方法均被应用于为处理车辆极限工况下的模型失配问题,并且非线性预测方法往往由于其高运算复杂度而导致算法实时性能不佳,局部线性化或分段仿射方法虽然能够保证算法的实时性,但这些方法难以避免地导致控制策略在不同线性化区间之内来回切换,使得人机交互结果产生不平滑现象,甚至出现在线性分段点附近来回切换的滑模现象;另一方面,对于多智能体动力学系统
而言,也可以采用动态非合作型博弈理论,但当前博弈理论在共驾系统中的研究主要局限在共享控制策略的设计,对于人机决策分歧与控制冲突间的映射关系尚无完善的理论描述。
45.为解决这一棘手问题,本公开针对决策分歧到控制冲突的人机交互机理进行研究。由于在人机耦合的转向动力学系统中,同时存在确定的转向阻力矩和驾驶员不确定的转向性力矩两种干扰,因此本公开提出新的随机博弈理论框架,考虑确定性和随机性的转向力矩,并拟通过不同信息模式下的纳什以及斯塔克博格均衡对这一映射关系进行完整描述,以设计连接人机决策分歧与控制冲突的理论桥梁,克服共驾系统存在的人机决策混淆问题,进而为共享控制策略设计提供理论依据。
46.以下对本公开实施例的技术方案的实现细节进行详细阐述。
47.图1示意性示出本公开示例性实施例中一种人机共驾冲突控制方法的流程示意图。如图1所示,该人机共驾冲突控制方法包括步骤s101至步骤s103:
48.步骤s101,基于驾驶员的确定性转向力矩和驾驶员的随机性转向力矩建立人机交互行为对应的人机路径跟踪控制博弈模型;
49.步骤s102,求解所述人机路径跟踪控制博弈模型得到人机力矩冲突信息;
50.步骤s103,根据所述人机力矩冲突信息确定共享控制策略,以根据所述共享控制策略进行车辆控制。
51.在本公开的一些实施例所提供的技术方案中,本公开基于驾驶员的确定性转向力矩和驾驶员的随机性转向力矩建立人机交互行为对应的人机路径跟踪控制博弈模型,并对人机路径跟踪控制博弈模型进行求解,以得到人机力矩冲突信息用于车辆控制,一方面能够对将驾驶员的不确定行为纳入人机路径跟踪控制,使其更符合实际场景需求,控制效果更加精准;另一方面,求解博弈模型得到的人机力矩冲突信息是对人机共驾模型中决策分歧到控制冲突的人机交互行为的精确描述,能够克服共驾系统存在的人机决策混淆问题,进而为共享控制策略设计提供理论依据,进一步优化车辆控制的结果。
52.下面,将结合附图及实施例对本示例实施方式中的人机共驾冲突控制方法的各个步骤进行更详细的说明。
53.在步骤s101中,基于驾驶员的确定性转向力矩和驾驶员的随机性转向力矩建立人机交互行为对应的人机路径跟踪控制博弈模型。
54.在本公开的一个实施例中,首先构建求解人机交互行为的人机路径跟踪控制博弈模型,人机路径跟踪控制博弈模型可以采用非合作型博弈理论框架。
55.图2示意性示出本公开示例性实施例中一种人机共驾系统的转向交互的原理示意图。如图2所示,驾驶员与自动驾驶系统(后续简称为驾驶系统)都会根据自身的目标轨迹产生相应的转向操纵行为,同时由于二者可以通过转向系统及整车运动状态感知双方决策,因此对于驾驶员而言,为达成自身决策目标,其转向操纵行为还包含了对驾驶系统转向行为做出的反应,因此在设计驾驶系统控制器时,也应当充分考虑驾驶员的转向控制输入。所以在人机共驾系统中,对人机转向冲突的建模必须考虑人机转向行为的交互,尤其在人机决策目标分歧条件下,驾驶员的转向行为不仅基于自身决策目标,还会对自动驾驶系统的转向行为进行主动补偿,与纯人工驾驶有着较大区别。
56.由于共驾过程中驾驶员和自动驾驶系统的转向行为都以极小化各轨迹跟踪误差
为目标,依据车路系统状态反馈以及对方的转向动作来产生各自转向动作,而人机各自决策层的目标轨迹难免出现分歧,在这种条件下的人机交互过程即可通过非合作型博弈理论框架进行描述。
57.图3示意性示出本公开示例性实施例中一种人机共驾系统的非合作型博弈的原理示意图。如图3所示,将驾驶员与驾驶系统视为博弈参与者,双方均以最大化各自利益为目标,综合博弈过程的状态信息以及对方动作来产生各自的动作。
58.当以博弈理论研究人机共驾问题时,运用基于代价函数的最优控制策略描述驾驶员与自动驾驶系统的轨迹跟踪行为,由于二者代价函数总和非零值,且由于最优轨迹跟踪控制通常采用预测及控制时域进行描述,因此人机共驾的轨迹跟踪问题可以抽象为非零和的多阶段动态博弈问题。对于非零和的多阶段动态博弈而言,可以根据博弈的信息模式将博弈问题分为闭环无记忆动态博弈问题和开环动态博弈问题两类。
59.图4示意性示出本公开示例性实施例中一种人机共驾系统的闭环动态博弈原理图。如图4所示,在该信息模式下,参与者的容许策略集则通过初始状态及各阶段的状态进行映射,而“无记忆”则指的是参与者在每个阶段作决策时仅知道系统初始及当前状态,对于其余各阶段的状态并无记忆,因此参与者在第i阶段的动作可以表达为i∈{0,1,
…
,nu}。
60.与闭环无记忆动态博弈相对应的则是开环动态博弈。图5示意性示出本公开示例性实施例中一种人机共驾系统的开环动态博弈的原理示意图。如图5所示,整个博弈过程共分为nu个阶段,各阶段系统的状态向量为xk,各阶段参与者的容许策略集仅与初始状态相关,因此当初始状态x0给定时,策略集为常值函数,而参与者的在第i阶段的动作也成为定常值i∈{0,1,
…
,nu}。
61.因此,在步骤s101中可以分别构建闭环和开环两种不同信息模式下的人机路径跟踪控制博弈模型。
62.①
闭环人机路径跟踪控制博弈模型
63.图6示意性示出本公开示例性实施例中一种构建闭环人机路径跟踪控制博弈模型方法的流程示意图,即采用最优多点预瞄的线性二次型调节器(linear quadratic regulator,lqr)方法来描述驾驶员和驾驶系统的转向行为。如图6所示,该构建人机路径跟踪控制博弈模型方法包括以下步骤:
64.步骤s601,基于所述驾驶员的确定性转向力矩和驾驶员的随机性转向力矩建立人机共驾车辆动力学系统在闭环信息模式下的第一离散状态更新方程;
65.步骤s602,通过人机预瞄动态过程对所述第一离散状态更新方程进行增广,得到包含人机预瞄状态的路径跟踪增广系统;
66.步骤s603,基于所述路径跟踪增广系统构造驾驶员轨迹代价函数和驾驶系统轨迹代价函数,以得到所述人机路径跟踪控制博弈模型。
67.具体而言,本节重点研究人机交互建模问题,因此可以假设人机目标轨迹均具有较小的切线方向角,在小航向角条件下,模型中的状态向量可简化为其中,θ
sw
为,为θ
sw
对时间的求导结果,y为车辆质心的全局纵坐标,ψ为车辆航向角,为ψ对时间的求导结果。
68.在步骤s601中,基于所述驾驶员的确定性转向力矩和驾驶员的随机性转向力矩建立人机共驾车辆动力学系统在闭环信息模式下的第一离散状态更新方程。
69.将驾驶员的确定性转向力矩记为τh,随机性转向力矩记为τ
hsto
,驾驶系统的转向力矩记为τm。基于状态向量xc、驾驶员的确定性转向力矩τh和驾驶员的随机性转向力矩τ
hsto
建立连续状态空间方程如公式(1)所示:
[0070][0071]
式中:τ
disk
为与距离相关的转向力矩,ac、bh、bm、nc以及cc都是模型中的参数矩阵,如下所示:
[0072][0073]
为了将人机共驾问题描述为多阶段博弈,通过系统离散时间ts对上式连续系统的离散化,人机共享型车辆动力学系统可以变为如下差分方程的形式,即第一离散状态更新方程,如公式(2)所示:
[0074][0075]
式中:式中:为人机共驾系统k时刻驾驶员的确定性转向力矩,为k时刻驾驶系统的转向力矩,τ
hsto
为驾驶员的随机性转向力矩,τ
disk
为与距离相关的转向力矩。
[0076]
在步骤s602中,通过人机预瞄动态过程对所述第一离散状态更新方程进行增广,得到包含人机预瞄状态的路径跟踪增广系统。
[0077]
图7示意性示出本公开示例性实施例中一种多点预瞄模式的原理示意图。为了采用基于lqr方法对路径跟踪控制系统进行建模,并考虑人机对车辆动力学的预测行为,首先将人机预瞄行为建模为如图7所示的多点预瞄模式。参考图7所示,驾驶员和驾驶系统在每一时刻都根据自身决策对其目标轨迹的一段区域进行预瞄,该区域可描述为n
p
个预瞄点,其预瞄距离由驾驶员的预瞄时间t
p
决定,且t
p
=n
p
×
ts。该动态过程可用移位寄存器表达,如公式(3)所示:
[0078][0079]
式中:r
x(k+i)
=[y
x
(k+i)ψ
x
(k+i)]
t
,,x∈{h,m},
[0080][0081]
通过人机预瞄动态过程对人机共享型车辆动力学系统进行增广,可得到包含人机预瞄状态的路径跟踪增广系统,如公式(4)所示:
[0082][0083]
式中:xk=[x
ck r
hk r
mk
]
t
,
[0084][0085]
在公式(4)中,设ck=nτ
disk
,,为驾驶员及驾驶系统预瞄区域最远端预瞄点的侧向位移以及航向角,由于驾驶员及驾驶系统在其余区域的预瞄信息均位于增广状态xk中,因此可略去最远端预瞄点信息路径跟踪增广系统可进一步简化为如公式(5)所示:
[0086][0087]
步骤s603,基于所述路径跟踪增广系统构造驾驶员轨迹代价函数和驾驶系统轨迹代价函数,以得到所述人机路径跟踪控制博弈模型。
[0088]
具体地,在人机决策分歧的路径跟踪增广系统中,设计预测及控制时域均为nu步长的驾驶员轨迹代价函数j1和驾驶系统轨迹代价函数j2,以得到人机路径跟踪控制博弈模型可描述为如公式(6)所示:
[0089][0090]
式中:
[0091][0092][0093]
其中,q1、q2分别为驾驶员和驾驶系统的状态加权矩阵,w1、w2分别为驾驶员和驾驶系统的跟踪误差加权矩阵,分别为驾驶员的车辆侧向跟踪误差和航向角误差的加权系数,分别为驾驶系统的车辆侧向跟踪误差和航向角误差的加权系数,r
11
、r
22
分别为驾驶员和驾驶系统的自身的输入加权系数,r
11
=q
u1
,r
22
=q
u2
,r
12
、r
21
分别为驾驶员和驾驶系统的交互输入加权系数,r
12
=q
u12
,r
21
=q
u21
。
[0094]
基于此,公式(6)通过线性二次型方法建立了nu阶段的人机路径跟踪控制博弈模型,双方的代价函数均包含了对方转向控制输入以表达人机交互特性。
[0095]
②
开环人机路径跟踪控制博弈模型
[0096]
图8示意性示出本公开示例性实施例中一种构建开环人机路径跟踪控制博弈模型方法的流程示意图,即采用分布式模型预测控制(distributed modelpredictive control,dmpc)策略描述开环信息模式下人机决策分歧与转向力矩冲突的映射关系。如图8所示,该构建人机路径跟踪控制博弈模型方法包括以下步骤:
[0097]
步骤s801,基于所述驾驶员的确定性转向力矩和驾驶员的随机性转向力矩建立人机共驾车辆动力学系统在开环信息模式下的第二离散状态更新方程;
[0098]
步骤s802,根据所述第二离散状态更新方程确定预测时域内的预测输出向量,并确定驾驶员参考轨迹向量和驾驶系统参考轨迹向量;
[0099]
步骤s803,利用所述预测输出向量、所述驾驶员参考轨迹向量和驾驶系统参考轨迹向量分别构造驾驶员轨迹代价函数和驾驶系统轨迹代价函数,以得到所述人机路径跟踪控制博弈模型。
[0100]
具体而言,在模型预测控制框架下,驾驶员与驾驶系统都在预测时域n
p
内对车辆运行轨迹进行估计,并且在控制属于nu内施加转向控制极小化车辆轨迹与各自决策之间的偏差,相比于线性二次型调节器方法,模型预测控制更直观地在最终的交互模型中反映驾驶员与自动驾驶系统决策层规划的目标轨迹。同时,由模型预测控制算法可知,其代价函数中状态预测向量的建立均基于系统当前状态及控制时域nu内的控制输入,因此控制律也仅与当前的初始状态相关,恰好符合开环信息模式的定义。
[0101]
在步骤s801中,基于所述驾驶员的确定性转向力矩和驾驶员的随机性转向力矩建立人机共驾车辆动力学系统在开环信息模式下的第二离散状态更新方程。
[0102]
对人机共驾型车辆动力学系统而言,将驾驶员不确定行为并入系统干扰,则得到第二离散状态更新方程如公式(7)所示:
[0103][0104]
式中:式中:为人机共驾系统k时刻驾驶员的确定性转向力矩,为k时刻驾驶系统的转向力矩,τ
hsto
为驾驶员的随机性转向力矩,τ
disk
为与距离相关的转向力矩,并记干扰输入w’k
=(τ
disk-τ
hsto
)。
[0105]
基于上述的第二离散状态更新方程,若假设预测时域内干扰输入w’k
保持不变,则人机共驾系统接下来n
p
步长的模型输出可以表达为:
[0106][0107]
步骤s802,根据所述第二离散状态更新方程确定预测时域内的预测输出向量,并确定驾驶员参考轨迹向量和驾驶系统参考轨迹向量。
[0108]
假设人机共驾系统模型预测算法的预测时域和控制时域均为nu,在k时刻,定义预测时域内的模型预测输出向量为y
pk
,如公式(8)所示,人机控制输入向量分别为u
hk
和u
mk
分别如公式(9)和公式(10)所示:
[0109][0110][0111][0112]
基于第二离散状态更新方程(式7),人机共驾系统接下来n
p
步长的模型输出,即预测输出向量可以表达为如公式(11):
[0113]ypk
=ψx
ck
+θhu
hk
+θmu
mk
+sw’k
(11)
[0114]
式中:
[0115][0116][0117]
[0118]
在每个时间步长k,驾驶员和自动驾驶系统的参考轨迹向量可以表达为如公式(12)所示:
[0119][0120]
步骤s803,利用所述预测输出向量、所述驾驶员参考轨迹向量和驾驶系统参考轨迹向量分别构造驾驶员轨迹代价函数和驾驶系统轨迹代价函数,以得到所述人机路径跟踪控制博弈模型。
[0121]
将人机路径跟踪控制博弈模型中的参数采用预测输出向量y
pk
以及参考轨迹向量r
hk
、r
mk
表示,得到驾驶员轨迹代价函数和驾驶系统轨迹代价函数如公式(13)所示:
[0122][0123]
式中:γ
yx
、γ
ux
都是路径跟踪控制的加权矩阵,其中x∈{1,2},
[0124][0125]
步骤s102,求解所述人机路径跟踪控制博弈模型得到人机力矩冲突信息。
[0126]
由于在步骤s101中,分别构建闭环和开环两种不同信息模式下的人机路径跟踪控制博弈模型,对于这两种博弈模型求解方式也有所不同。
[0127]
另外,对于非合作型博弈问题,由于人机共驾系统中,通常采用镜像对称的拟人化策略设计自动驾驶系统控制器以提升人机一致性,因此驾驶员与自动驾驶系统在博弈过程中具有对等关系,当博弈参与者处于对称或平等关系时,纳什均衡(nash equilibrium)为非合作型博弈提供了一种合理的理论解,在该平衡状态下没有任何一方对决策过程占据主导地位,且任何一方都不可能通过单方面调整自身决策而达到降低自己的轨迹跟踪代价函数值。
[0128]
此外还存在另一种类型的非合作型博弈问题,即双智能体系统的主从式博弈问题,在该问题中主导者了解跟随者对自己所做决策的反应,并且首先做出决策,而跟随者在观察主导者的决策后再做出相应的决策。这种分层式博弈结果称为斯塔克博格均衡(stackelberg equilibrium)。
[0129]
由于纳什均衡和斯塔克博格均衡可以从理论上对人机共驾系统决策-控制机理进行建模,对于每一种博弈模型都可以求出该模型对应的纳什均衡和斯塔克博格均衡两种解。因此接下来拟采用四种基于非合作型博弈理论的量化模型,基于开环和闭环两种信息模式,深入分析纳什均衡、斯塔克博格均衡下人机决策分歧与转向力矩冲突间的映射关系,以探索人机交互机理的最佳建模方式建模方法。
[0130]
①
闭环信息模式下的人机决策-控制纳什均衡解
[0131]
在本公开的一个实施例中,可将闭环信息模式下纳什均衡的求解问题描述为如公式(14)所示的哈密顿函数约束优化问题:
[0132][0133]
式中:为协态向量。
[0134]
上式约束优化问题的闭式解构成闭环纳什均衡解。
[0135]
开环模式下的纳什均衡解仅与初始状态相关,与各阶段的当前状态无关,因此开环纳什均衡解也满足闭环纳什均衡条件(14),但显然闭环纳什均衡问题的解并不只有开环纳什均衡解,这种信息非唯一性就导致了闭环信息结构下纳什均衡的多解问题。由于本文在系统建模时考虑了驾驶员随机转向力矩的参数θk,恰好消除了博弈过程中的信息非唯一性,因此可以通过反馈纳什均衡以避免多解问题,反馈纳什均衡各阶段最优解分别满足如下条件:
[0136][0137]
可见闭环条件下的反馈纳什均衡条件符合贝尔曼(bellman)最优性原理,可以通过随机动态规划法(stochastic dynamic programming,sdp)算法求解人机决策分歧条件下路径跟踪控制系统的闭环纳什均衡解(也可称为反馈纳什均衡解)。
[0138]
图9示意性示出本公开示例性实施例中一种求解闭环人机路径跟踪控制博弈模型方法的流程示意图。如图9所示,该求解人机路径跟踪控制博弈模型方法包括以下步骤:
[0139]
步骤s901,采用随机动态规划算法确定纳什均衡条件下的驾驶员和驾驶系统分别对应的转向控制值函数的递归关系;
[0140]
步骤s902,基于所述第一离散状态更新方程和所述递归关系计算驾驶员和驾驶系统分别对应的闭环纳什均衡解作为所述人机力矩冲突信息。
[0141]
具体而言,在任一时间步长k时,假定人机共驾系统未建模干扰ck在整个nu阶段的
动态博弈中保持不变,而运用高斯随机分布θk~n(μ,σ)描述关于驾驶员随机转向力矩的参数,式中μ、σ分别代表高斯分布的均值和标准差。
[0142]
由于干扰向量干扰向量ck、θk的存在,使得基于转向力矩交互的人机博弈问题的求解变为一个仿射二次型问题,因此在动态规划求解过程中,驾驶员及驾驶系统的转向控制值函数具备如下仿射二次型形式如公式(15)所示:
[0143][0144]
上述式(15)中的转向控制值函数表示了驾驶员及驾驶系统各自的代价函数由第j阶段至第nu阶段博弈过程中值函数的值,第k+j步与第k+j+1步的转向控制值函数满足递归关系如公式(16)所示:
[0145][0146]
式中,上标“n”代表纳什均衡条件下的值函数,而每一阶段的单步代价函数g()可以表达为如公式(17)所示:
[0147][0148]
将第一离散状态更新方程(式4)代入转向控制值函数(式15),可得到满足闭环纳什均衡关系的人机力矩满足关系如公式(18)所示::
[0149][0150]
②
闭环信息模式下的人机决策-控制斯塔克博格均衡解
[0151]
图10示意性示出本公开示例性实施例中另一种求解闭环人机路径跟踪控制博弈模型方法的流程示意图。如图10所示,该求解人机路径跟踪控制博弈模型方法包括以下步骤:
[0152]
步骤s1001,采用随机动态规划算法确定斯塔克博格均衡条件下的驾驶员和驾驶系统分别对应的转向控制值函数的递归关系;
[0153]
步骤s1002,根据驾驶系统对应的转向控制值函数的递归关系确定驾驶员反应函数;
[0154]
步骤s1003,基于所述第一离散状态更新方程、所述驾驶员反应函数以及驾驶系统对应的转向控制值函数的递归关系计算驾驶系统对应的开环斯塔克博格均衡解;
[0155]
步骤s1004,根据所述驾驶系统对应的开环斯塔克博格均衡解计算驾驶员对应的开环斯塔克博格均衡解,以作为所述人机力矩冲突信息。
[0156]
具体而言,区别于纳什均衡,在斯塔克博格均衡中,驾驶员与自动驾驶系统之间存在主从关系。在博弈的每一个阶段,作为主导者的驾驶系统首先采取转向控制输入,驾驶员观察这一动作并且做出相应的反应。
[0157]
因此,闭环斯塔克博格均衡解可通过逆向归纳法(backward induction)进行求解。基于随机动态规划方法,驾驶员转向控制值函数递归关系与(参见式16)相同。
[0158]
而闭环信息模式下的闭环斯塔克博格均衡解(也可称为反馈斯塔克博格均衡解)中驾驶系统转向控制值函数递归关系满足条件如公式(19)所示:
[0159][0160]
式中,上标“s”代表斯塔克博格均衡条件下的值函数,其中,
[0161][0162]
将第一离散状态更新方程(式4)和驾驶员转向控制值函数递归关系代入驾驶系统转向控制值函数递归关系(式19)可以求出驾驶员关于驾驶系统转向力矩的反应函数,如公式(20)所示:
[0163][0164]
通过将第一离散状态更新方程(式4)和驾驶员反应函数(式20)代入驾驶系统转向控制值函数递归关系(式19),则驾驶系统在斯塔克博格均衡策略下的开环斯塔克博格均衡解如公式(21)所示:
[0165][0166]
式中:式中:
[0167]
由于驾驶系统为主导者,驾驶员为跟随者,所以随后可以将驾驶系统的开环斯塔克博格均衡解求出驾驶员相应的哈密顿函数约束优化问题求出闭式解作为驾驶员的开环斯塔克博格均衡解。
[0168]
③
开环信息模式下的人机决策-控制纳什均衡解
[0169]
图11示意性示出本公开示例性实施例中另一种求解开环人机路径跟踪控制博弈模型方法的流程示意图。如图11所示,该求解人机路径跟踪控制博弈模型方法包括以下步骤:
[0170]
步骤s1101,求解所述人机路径跟踪控制博弈模型对应的模型闭式解,以根据所述模型闭式解得到人机转向控制与目标轨迹间的关系表达式;
[0171]
步骤s1102,采用凸迭代算法求解所述关系表达式得到驾驶员和驾驶系统分别对
应的开环纳什均衡解作为所述人机力矩冲突信息。
[0172]
具体而言,基于开环纳什均衡的定义,采用凸迭代算法求解系统在开环信息模式下的纳什均衡解。
[0173]
对于如公式(13)的无约束问题,人机路径跟踪控制律具有如下闭式解,见公式(22):
[0174][0175]
式中:
[0176][0177]
其中,pinv()为伪逆算子,pinv(a)=(a
t
a)-1at
,因此得到人机转向控制与目标轨迹间的关系表达式,见公式(23):
[0178][0179]
由公式(23)可见二者控制律存在交互耦合关系,即自身控制行为不仅与各自决策目标、系统状态、干扰有关,同时还与对方控制策略密切相关。因此,为了实现公式(23)解耦,采用凸迭代算法对其进行求解,得到更新公式如公式(24)所示:
[0180][0181]
凸迭代算法的求解过程可以总结为:首先确定迭代初值u
hk(0)
、u
mk(0)
,随后代入关系表达式(式23)即可求得当前最优值再代入更新公式(式24)中,更新下一步u
hk(1)
、u
mk(1)
,如此迭代循环下去。当i趋近于无穷大时,更新公式(式24)变为:
[0182][0183]
因此,关系表达式(式23)变为:
[0184][0185]
所以开环信息模式下人机决策-控制纳什均衡解的表达式如公式(27)所示:
[0186][0187]
在实际建模过程中,取博弈第一阶段的值作为k时刻开环纳什均衡的人机交互结
果,即人机力矩冲突信息:
[0188][0189]
④
开环信息模式下的人机决策-控制斯塔克博格均衡解
[0190]
图12示意性示出本公开示例性实施例中另一种求解开环人机路径跟踪控制博弈模型方法的流程示意图。如图12所示,该求解人机路径跟踪控制博弈模型方法包括以下步骤:
[0191]
步骤s1201,将所述驾驶系统轨迹代价函数转换为考虑驾驶员反应函数的驾驶系统轨迹优化函数;
[0192]
步骤s1202,求解所述驾驶系统轨迹优化函数得到驾驶系统对应的开环斯塔克博格均衡解;
[0193]
步骤s1203,基于所述开环斯塔克博格均衡解和驾驶员轨迹代价函数计算驾驶员对应的开环斯塔克博格均衡解,以作为所述人机力矩冲突信息。
[0194]
具体而言,开环斯塔克博格均衡解采用与闭环斯塔克博格均衡求解相类似的逆向归纳法实现。将预测输出向量y
pk
(式11)代入博弈模型(式13)中可得:
[0195][0196]
式中,e
hk
=r
hk-ψx
ck-sdw’k-θmu
mk
,e
mk
=r
mk-ψx
ck-sdw’k-θhu
hk
。
[0197]
与开环纳什均衡求解不同,在主从式博弈当中,在每一阶段博弈过程中自动驾驶系统作为主导者首先采取行动,驾驶员在观测到自动驾驶系统动作后再做出相应的反应。
[0198]
因此,通过求解j1获得驾驶员对驾驶系统的反应函数,如公式(30)所示:
[0199][0200]
当采取控制策略时,驾驶系统将驾驶员对它的反应函数考虑进它的代价函数得到新的驾驶系统轨迹代价函数,如公式(31)所示:
[0201]
j2=||γ
y2
[θmu
mk-r
mk
+ψx
ck
+sdw’k
+θhl
hkehk
]||2+||γ
u2umk
||2(31)
[0202]
因此,求解开环信息模式下驾驶系统转向力矩控制的斯塔克博格均衡解就变为求如公式(32)所示的无约束优化问题的求解:
[0203][0204]
通过求解上述优化问题,可以得到驾驶系统对应的开环斯塔克博格均衡解如公式(33)所示:
[0205][0206]
式中:ψ’m
=ψ-θhl
hk
ψ,s’m
=s-θhlhsd,θ’m
=θhlh,θ’m1
=θ
m-θhlhθm,
[0207]
基于驾驶系统转向控制的斯塔克博格均衡解驾驶员对自动驾驶系统转向控制的最优响应即可通过求解如公式(34)的优化问题得到:
[0208][0209]
通过上式可以得出开环信息模式下驾驶员转向控制的斯塔克博格均衡解如公式(35)所示:
[0210][0211]
式中:t1’
=i+θml’m
θ’m
,θ’h
=θml’m
,ψ
’1=-ψ+θml’m
ψ’m
,s
’1=-s+θml’m
s’m
[0212]
类似地,取博弈第一阶段的开环斯塔克博格均衡解描述k时刻的人机转向力矩交互结果如公式(36)所示:
[0213][0214]
与开环纳什均衡不同的是,由于开环斯塔克博格均衡的求解基于逆向归纳法实现,因此在求解自动驾驶系统控制律(式34)时,还可以通过增加约束使之变为约束优化问题,从而使得控制器满足预期性能,因此本文所提出的开环斯塔克博格均衡策略的意义不仅在于提出一种人机转向力矩交互的理论模型,同时可以应用该算法灵活地设计满足运动学、动力学安全约束的交互式转向辅助控制器。
[0215]
在步骤s103中,根据所述人机力矩冲突信息确定共享控制策略,以根据所述共享控制策略进行车辆控制。
[0216]
具体地,步骤s102得到的人机力矩冲突信息为人机决策分歧与控制冲突之间建立了理论基础,基于此理论基础可以更好地设计紧急换道工况下的共享控制策略设计,以此来指导车辆控制。
[0217]
本公开为建立人机决策分歧与控制冲突之间的理论关系,分别通过四种动态非合作型博弈的理论框架对人机决策分歧与人机转向力矩交互间的映射关系进行了建模。
[0218]
一方面,通过人机目标轨迹对共驾系统动力学模型进行增广,随后通过线性二次型调节器方法对反馈信息模式下的人机交互行为进行建模。
[0219]
由于模型建立的是人机决策分歧与转向力矩交互的映射关系,转向阻力矩以及驾驶员不确定性力矩的存在使得人机决策分歧问题的求解变为了仿射二次型博弈问题,因此本文提出基于随机动态规划的仿射二次型博弈算法,求出了描述人机决策与转向力矩交互关系的反馈纳什均衡解、反馈斯塔克博格均衡解。
[0220]
另一方面,采用分布式模型预测控制方法来描述开环下的人车多目标路径跟踪控制问题,为了求解开环信息模式下的人机决策-控制模型,又进一步通过模型预测控制方法求解了描述人机决策与控制映射关系的开环纳什均衡解、开环斯塔克博格均衡解。
[0221]
图13示意性示出本公开示例性实施例中一种人机共驾冲突控制装置的组成示意图,如图13所示,该人机共驾冲突控制装置1300可以包括建模模块1301、求解模块1302以及运用模块1303。其中:
[0222]
建模模块1301,用于基于驾驶员的确定性转向力矩和驾驶员的随机性转向力矩建立人机交互行为对应的人机路径跟踪控制博弈模型;
[0223]
求解模块1302,用于求解所述人机路径跟踪控制博弈模型得到人机力矩冲突信息;
[0224]
运用模块1303,用于根据所述人机力矩冲突信息确定共享控制策略,以根据所述共享控制策略进行车辆控制。
[0225]
根据本公开的示例性实施例,所述建模模块1301包括第一建模单元,用于基于所述驾驶员的确定性转向力矩和驾驶员的随机性转向力矩建立人机共驾车辆动力学系统在闭环信息模式下的第一离散状态更新方程;通过人机预瞄动态过程对所述第一离散状态更新方程进行增广,得到包含人机预瞄状态的路径跟踪增广系统;基于所述路径跟踪增广系统构造驾驶员轨迹代价函数和驾驶系统轨迹代价函数,以得到所述人机路径跟踪控制博弈模型。
[0226]
根据本公开的示例性实施例,所述建模模块1301包括第二建模单元,用于基于所述驾驶员的确定性转向力矩和驾驶员的随机性转向力矩建立人机共驾车辆动力学系统在开环信息模式下的第二离散状态更新方程;根据所述第二离散状态更新方程确定预测时域内的预测输出向量,并确定驾驶员参考轨迹向量和驾驶系统参考轨迹向量;利用所述预测输出向量、所述驾驶员参考轨迹向量和驾驶系统参考轨迹向量分别构造驾驶员轨迹代价函数和驾驶系统轨迹代价函数,以得到所述人机路径跟踪控制博弈模型。
[0227]
根据本公开的示例性实施例,所述求解模块1302包括第一求解单元,用于采用随机动态规划算法确定纳什均衡条件下的驾驶员和驾驶系统分别对应的转向控制值函数的递归关系;基于所述第一离散状态更新方程和所述递归关系计算驾驶员和驾驶系统分别对应的闭环纳什均衡解作为所述人机力矩冲突信息。
[0228]
根据本公开的示例性实施例,所述求解模块1302包括第二求解单元,用于采用随机动态规划算法确定斯塔克博格均衡条件下的驾驶员和驾驶系统分别对应的转向控制值函数的递归关系;根据驾驶系统对应的转向控制值函数的递归关系确定驾驶员反应函数;基于所述第一离散状态更新方程、所述驾驶员反应函数以及驾驶系统对应的转向控制值函数的递归关系计算驾驶系统对应的开环斯塔克博格均衡解;根据所述驾驶系统对应的开环斯塔克博格均衡解计算驾驶员对应的开环斯塔克博格均衡解,以作为所述人机力矩冲突信息。
[0229]
根据本公开的示例性实施例,所述求解模块1302包括第三求解单元,用于求解所述人机路径跟踪控制博弈模型对应的模型闭式解,以根据所述模型闭式解得到人机转向控制与目标轨迹间的关系表达式;采用凸迭代算法求解所述关系表达式得到驾驶员和驾驶系统分别对应的开环纳什均衡解作为所述人机力矩冲突信息。
[0230]
根据本公开的示例性实施例,所述求解模块1302包括第四求解单元,用于将所述驾驶系统轨迹代价函数转换为考虑驾驶员反应函数的驾驶系统轨迹优化函数;求解所述驾驶系统轨迹优化函数得到驾驶系统对应的开环斯塔克博格均衡解;基于所述开环斯塔克博格均衡解和驾驶员轨迹代价函数计算驾驶员对应的开环斯塔克博格均衡解,以作为所述人机力矩冲突信息。
[0231]
上述的人机共驾冲突控制装置1300中各模块的具体细节已经在对应的人机共驾冲突控制方法中进行了详细的描述,因此此处不再赘述。
[0232]
应当注意,尽管在上文详细描述中提及了用于动作执行的设备的若干模块或者单元,但是这种划分并非强制性的。实际上,根据本公开的实施方式,上文描述的两个或更多模块或者单元的特征和功能可以在一个模块或者单元中具体化。反之,上文描述的一个模块或者单元的特征和功能可以进一步划分为由多个模块或者单元来具体化。
[0233]
在本公开的示例性实施例中,还提供了一种能够实现上述方法的存储介质。图14示意性示出本公开示例性实施例中一种计算机可读存储介质的示意图,如图14所示,描述了根据本公开的实施方式的用于实现上述方法的程序产品1400,其可以采用便携式紧凑盘只读存储器(cd-rom)并包括程序代码,并可以在终端设备,例如手机上运行。然而,本公开的程序产品不限于此,在本文件中,可读存储介质可以是任何包含或存储程序的有形介质,该程序可以被指令执行系统、装置或者器件使用或者与其结合使用。
[0234]
在本公开的示例性实施例中,还提供了一种能够实现上述方法的电子设备。图15示意性示出本公开示例性实施例中一种电子设备的计算机系统的结构示意图。
[0235]
需要说明的是,图15示出的电子设备的计算机系统1500仅是一个示例,不应对本公开实施例的功能和使用范围带来任何限制。
[0236]
如图15所示,计算机系统1500包括中央处理单元(central processing unit,cpu)1501,其可以根据存储在只读存储器(read-only memory,rom)1502中的程序或者从存储部分1508加载到随机访问存储器(random access memory,ram)1503中的程序而执行各种适当的动作和处理。在ram 1503中,还存储有系统操作所需的各种程序和数据。cpu 1501、rom 1502以及ram 1503通过总线1504彼此相连。输入/输出(input/output,i/o)接口1505也连接至总线1504。
[0237]
以下部件连接至i/o接口1505:包括键盘、鼠标等的输入部分1506;包括诸如阴极射线管(cathode ray tube,crt)、液晶显示器(liquid crystal display,lcd)等以及扬声器等的输出部分1507;包括硬盘等的存储部分1508;以及包括诸如lan(local area network,局域网)卡、调制解调器等的网络接口卡的通信部分1509。通信部分1509经由诸如因特网的网络执行通信处理。驱动器1510也根据需要连接至i/o接口1505。可拆卸介质1511,诸如磁盘、光盘、磁光盘、半导体存储器等等,根据需要安装在驱动器1510上,以便于从其上读出的计算机程序根据需要被安装入存储部分1508。
[0238]
特别地,根据本公开的实施例,下文参考流程图描述的过程可以被实现为计算机软件程序。例如,本公开的实施例包括一种计算机程序产品,其包括承载在计算机可读介质上的计算机程序,该计算机程序包含用于执行流程图所示的方法的程序代码。在这样的实施例中,该计算机程序可以通过通信部分1509从网络上被下载和安装,和/或从可拆卸介质1511被安装。在该计算机程序被中央处理单元(cpu)1501执行时,执行本公开的系统中限定
的各种功能。
[0239]
需要说明的是,本公开实施例所示的计算机可读介质可以是计算机可读信号介质或者计算机可读存储介质或者是上述两者的任意组合。计算机可读存储介质例如可以是——但不限于——电、磁、光、电磁、红外线、或半导体的系统、装置或器件,或者任意以上的组合。计算机可读存储介质的更具体的例子可以包括但不限于:具有一个或多个导线的电连接、便携式计算机磁盘、硬盘、随机访问存储器(ram)、只读存储器(rom)、可擦式可编程只读存储器(erasable programmable read only memory,eprom)、闪存、光纤、便携式紧凑磁盘只读存储器(compact disc read-only memory,cd-rom)、光存储器件、磁存储器件、或者上述的任意合适的组合。在本公开中,计算机可读存储介质可以是任何包含或存储程序的有形介质,该程序可以被指令执行系统、装置或者器件使用或者与其结合使用。而在本公开中,计算机可读的信号介质可以包括在基带中或者作为载波一部分传播的数据信号,其中承载了计算机可读的程序代码。这种传播的数据信号可以采用多种形式,包括但不限于电磁信号、光信号或上述的任意合适的组合。计算机可读的信号介质还可以是计算机可读存储介质以外的任何计算机可读介质,该计算机可读介质可以发送、传播或者传输用于由指令执行系统、装置或者器件使用或者与其结合使用的程序。计算机可读介质上包含的程序代码可以用任何适当的介质传输,包括但不限于:无线、有线等等,或者上述的任意合适的组合。
[0240]
附图中的流程图和框图,图示了按照本公开各种实施例的系统、方法和计算机程序产品的可能实现的体系架构、功能和操作。在这点上,流程图或框图中的每个方框可以代表一个模块、程序段、或代码的一部分,上述模块、程序段、或代码的一部分包含一个或多个用于实现规定的逻辑功能的可执行指令。也应当注意,在有些作为替换的实现中,方框中所标注的功能也可以以不同于附图中所标注的顺序发生。例如,两个接连地表示的方框实际上可以基本并行地执行,它们有时也可以按相反的顺序执行,这依所涉及的功能而定。也要注意的是,框图或流程图中的每个方框、以及框图或流程图中的方框的组合,可以用执行规定的功能或操作的专用的基于硬件的系统来实现,或者可以用专用硬件与计算机指令的组合来实现。
[0241]
描述于本公开实施例中所涉及到的单元可以通过软件的方式实现,也可以通过硬件的方式来实现,所描述的单元也可以设置在处理器中。其中,这些单元的名称在某种情况下并不构成对该单元本身的限定。
[0242]
作为另一方面,本公开还提供了一种计算机可读介质,该计算机可读介质可以是上述实施例中描述的电子设备中所包含的;也可以是单独存在,而未装配入该电子设备中。上述计算机可读介质承载有一个或者多个程序,当上述一个或者多个程序被一个该电子设备执行时,使得该电子设备实现上述实施例中所述的方法。
[0243]
应当注意,尽管在上文详细描述中提及了用于动作执行的设备的若干模块或者单元,但是这种划分并非强制性的。实际上,根据本公开的实施方式,上文描述的两个或更多模块或者单元的特征和功能可以在一个模块或者单元中具体化。反之,上文描述的一个模块或者单元的特征和功能可以进一步划分为由多个模块或者单元来具体化。
[0244]
通过以上的实施方式的描述,本领域的技术人员易于理解,这里描述的示例实施方式可以通过软件实现,也可以通过软件结合必要的硬件的方式来实现。因此,根据本公开
实施方式的技术方案可以以软件产品的形式体现出来,该软件产品可以存储在一个非易失性存储介质(可以是cd-rom,u盘,移动硬盘等)中或网络上,包括若干指令以使得一台计算设备(可以是个人计算机、服务器、触控终端、或者网络设备等)执行根据本公开实施方式的方法。
[0245]
本领域技术人员在考虑说明书及实践这里公开的发明后,将容易想到本公开的其它实施方案。本公开旨在涵盖本公开的任何变型、用途或者适应性变化,这些变型、用途或者适应性变化遵循本公开的一般性原理并包括本公开未公开的本技术领域中的公知常识或惯用技术手段。
[0246]
应当理解的是,本公开并不局限于上面已经描述并在附图中示出的精确结构,并且可以在不脱离其范围进行各种修改和改变。本公开的范围仅由所附的权利要求来限制。
相关技术
网友询问留言
已有0条留言
- 还没有人留言评论。精彩留言会获得点赞!
1