一种基于FFT的平面阵MIMO雷达波形设计方法与流程

本发明涉及雷达技术领域，尤其涉及一种基于FFT的平面阵MIMO雷达波形设计方法。

背景技术：

多输入多输出(Multiple-Input Multiple-Output，MIMO)雷达是目前正处在快速发展的新体制雷达，其在定位精度、对低速运动目标检测、空间分辨率以及对付隐形目标和低截获概率等方面具有传统雷达不可比拟的优势，已成为当前雷达技术领域的研究热点。由于MIMO雷达的每个发射天线可以独立发射不同的波形，因此相比与传统的相控阵雷达，MIMO雷达的发射信号设计更为灵活，系统的可利用自由度有所增加，大大改善了对目标参数的估计能力，提高了雷达可分辨的目标数目。

目前，已有的MIMO雷达波形设计方法主要基于迭代算法来计算发射信号的协方差矩阵，并以此来设计满足一定限制条件的一维MIMO雷达波形。现有的这种MIMO雷达波形设计方法不仅运算量大，且无法直接推广到平面阵MIMO雷达波形设计。

技术实现要素：

为此，本发明提供一种基于FFT的平面阵MIMO雷达波形设计方法，能够实现对平面阵MIMO雷达的波形设计，且运算量较小。

为达到上述目的，本发明采用如下技术方案：

提供一种一种基于FFT的平面阵MIMO雷达波形设计方法，其特征在于，包括以下步骤：

步骤1，建立MIMO雷达在笛卡尔坐标系XOYZ中的几何模型；其中，在MIMO雷达的几何模型中，MIMO雷达的发射阵列为二维均匀平面阵列，并位于笛卡尔坐标系XOYZ的XOY平面内，其中X轴包含M_x个阵元，阵元间距为d_x，Y轴包含M_y个阵元，阵元间距为d_y；二维均匀平面阵列的方位角范围为[Ω_min，Ω_max]，0°≤Ω_min＜Ω_max≤180°，俯仰角范围为[Γ_min，Γ_max]，且Γ_min＝-Γ_max，Γ_max∈[0，90°]；二维均匀平面阵列形成L个发射波束；

步骤2，按照固定间隔在二维均匀平面阵列的方位角范围[Ω_min，Ω_max]内均匀抽取K个方位角{θ₁，θ₂，…θ_K}，以及按照固定间隔在二维均匀平面阵列的俯仰角范围[Γ_min，Γ_max]内均匀抽取I个俯仰角K和I为正整数；

遍历K个方位角和I个俯仰角，对于K个方位角中的任一方位角θ_k和I个俯仰角中的任一俯仰角计算处的发射导向矢量得到K×I个发射导向矢量；其中，k和i为整数，1≤k≤K，1≤i≤I；

令l＝1；

步骤3，在方位角范围[Ω_min，Ω_max]内随机抽取两个数值构成第l个发射波束对应的方位角范围其中为在方位角范围[Ω_min，Ω_max]内随机抽取的两个数值中的较小值，为在方位角范围[Ω_min，Ω_max]内随机抽取的两个数值中的较大值；

在俯仰角范围[Γ_min，Γ_max]内随机抽取两个数值构成第l个发射波束对应的俯仰角范围其中为在俯仰角范围[Γ_min，Γ_max]内随机抽取的两个数值中的较小值，为在俯仰角范围[Γ_min，Γ_max]内随机抽取的两个数值中的较大值；

步骤4，利用第l个发射波束对应的方位角范围计算得到X轴上M_x个阵元发射信号的协方差矩阵

利用第l个发射波束对应的俯仰角范围计算得到Y轴上M_y个阵元发射信号的协方差矩阵

利用协方差矩阵及协方差矩阵计算得到第l个发射波束对应的协方差矩阵

步骤5，令l加1，重复执行步骤3-步骤4，直至l＝L，得到全部L个发射波束中各发射波束对应的协方差矩阵；

本发明实施例提供的基于FFT的平面阵MIMO雷达波形设计方法，首先，建立MIMO雷达在笛卡尔坐标系中的几何模型，并分别按照固定间隔在二维均匀平面阵列的方位角范围及俯仰角范围内均匀抽取多个方位角和俯仰角，对于其中的任一方位角和任一俯仰角，计算得到对应的发射导向矢量；接着，对于每一个发射波束，分别在二维均匀平面阵列的方位角范围及俯仰角范围内随机抽取两个数值构成对应的方位角范围及俯仰角范围，并利用构造得到的方位角范围计算得到X轴上的协方差矩阵，利用构造得到的俯仰角范围计算得到Y轴上的协方差矩阵，再利用X轴上的协方差矩阵和Y轴上的协方差矩阵计算得到该发射波束对应的协方差矩阵；进而利用所得的全部协方差矩阵及全部发射导向矢量计算得到MIMO雷达的方向图函数。

相比于现有技术，本发明上述方案能够实现对平面阵MIMO雷达的波形设计，且运算量较小。具体来说，本发明方法的运算复杂度为O(Nlog(N))，而现有的迭代算法的运算复杂度为(其中复杂度前缀η通常取)，可见，本发明方法的运算复杂度低于现有的迭代算法，因此基于本发明方法设计平面阵MIMO雷达的发射波形，运算量将较小。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。

图1为本发明实施例提供的一种基于FFT的平面阵MIMO雷达波形设计方法的流程示意图；

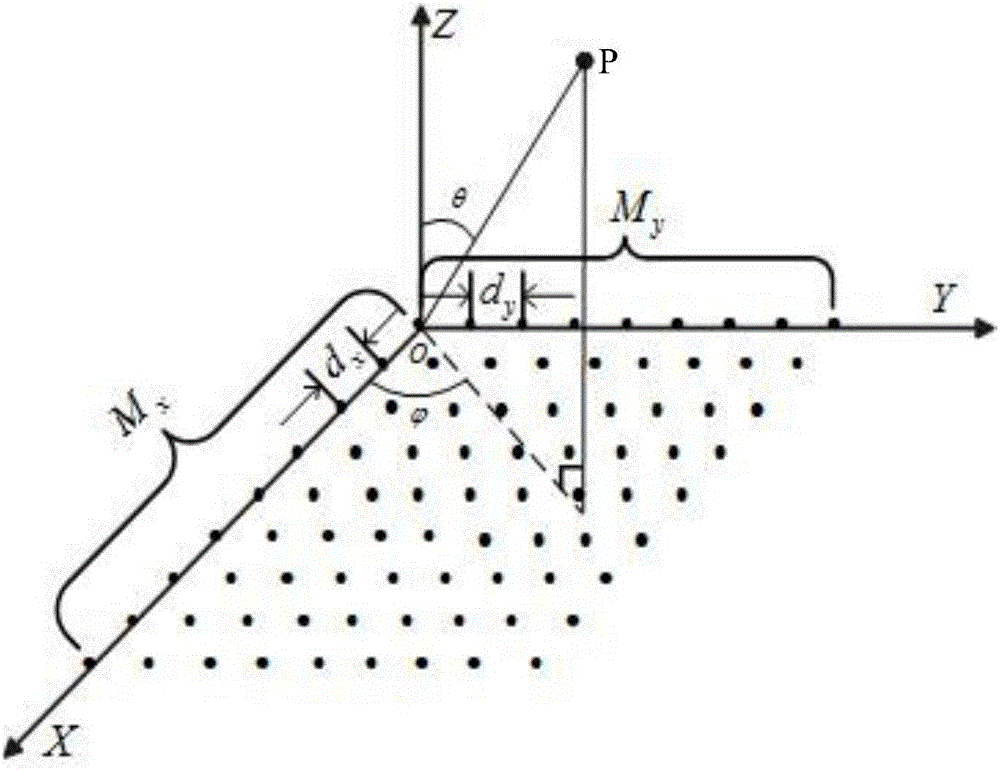
图2为MIMO雷达在笛卡尔坐标系中的几何模型示意图；

图3为采用本发明方法得到的MIMO雷达俯仰角维单波束方向图；

图4为采用本发明方法得到的MIMO雷达二维单波束方向图；

图5为采用本发明方法得到的MIMO雷达俯仰角维多波束方向图；

图6为采用本发明方法得到的MIMO雷达二维多波束方向图。

具体实施方式

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

图1所示为本发明实施例提供的一种基于FFT的平面阵MIMO雷达波形设计方法的流程示意图。

如图1所示，本发明实施例提供的一种基于FFT的平面阵MIMO雷达波形设计方法包括以下步骤：

一种基于FFT的平面阵MIMO雷达波形设计方法，其特征在于，包括以下步骤：

步骤1，建立MIMO雷达在笛卡尔坐标系XOYZ中的几何模型。

在MIMO雷达的几何模型中，MIMO雷达的发射阵列为二维均匀平面阵列，并位于笛卡尔坐标系XOYZ的XOY平面内，其中X轴包含M_x个阵元，阵元间距为d_x，Y轴包含M_y个阵元，阵元间距为d_y；二维均匀平面阵列的方位角范围为[Ω_min，Ω_max]，0°≤Ω_min＜Ω_max≤180°，俯仰角范围为[Γ_min，Γ_max]，且Γ_min＝-Γ_max，Γ_max∈[0，90°]，二维均匀平面阵列形成L个发射波束。

图2所示为MIMO雷达的几何模型，图中XOYZ表示笛卡尔坐标系，位于XOY平面内的实心原点表示阵元，点P表示目标，θ表示目标的方位角，表示目标的俯仰角，M_x表示X轴上的阵元个数，d_x表示X轴上的阵元间距，M_y表示Y轴上的阵元个数，d_y表示Y轴上阵元间距。

优选的，为防止出现栅瓣，本发明实施例优选M_x＝M_y，其中λ表示发射信号波长。

步骤2，在二维均匀平面阵列的方位角范围[Ω_min，Ω_max]内均匀抽取K个方位角{θ₁，θ₂，…θ_K}，以及在二维均匀平面阵列的俯仰角范围[Γ_min，Γ_max]内均匀抽取I个俯仰角进而遍历K个方位角和I个俯仰角，对于K个方位角中的任一方位角θ_k和I个俯仰角中的任一俯仰角计算处的发射导向矢量得到K×I个发射导向矢量，并令l＝1。

其中，k和i为整数，1≤k≤K，1≤i≤I，K和I为正整数。所述的均匀抽取是指，在已知方位角/俯仰角范围以及待抽取的方位角/俯仰角总个数(即K/I)后，计算出抽取间隔，按照该抽取间隔从方位角/俯仰角范围内均匀抽取方位角/俯仰角。

具体的，步骤2中，对于K个方位角中的任一方位角θ_k和I个俯仰角中的任一俯仰角计算对应的发射导向矢量具体可以包括如下步骤：

(2a)利用方位角θ_k和俯仰角计算得到X轴上的发射导向矢量

其中，k1∈{0，1，2，…，(M_x-1)}，e表示自然对数，表示Kronecker积，f_c表示MIMO雷达的发射信号载频，c表示光速，上标T表示转置。

(2b)利用俯仰角θ_k和方位角计算得到Y轴上的发射导向矢量

其中，k2∈{0，1，2，…，(M_y-1)}。

(2c)利用X轴上的发射导向矢量和Y轴上的发射导向矢量计算得到发射导向矢量

步骤3，在方位角范围[Ω_min，Ω_max]内随机抽取两个数值构成第l个发射波束对应的方位角范围以及在俯仰角范围[Γ_min，Γ_max]内随机抽取两个数值构成第l个发射波束对应的俯仰角范围

其中，为在方位角范围[Ω_min，Ω_max]内随机抽取的两个数值中的较小值，为在方位角范围[Ω_min，Ω_max]内随机抽取的两个数值中的较大值，为在俯仰角范围[Γ_min，Γ_max]内随机抽取的两个数值中的较小值，为在俯仰角范围[Γ_min，Γ_max]内随机抽取的两个数值中的较大值。

步骤4，利用第l个发射波束对应的方位角范围计算得到X轴上M_x个阵元发射信号的协方差矩阵利用第l个发射波束对应的俯仰角范围计算得到Y轴上M_y个阵元发射信号的协方差矩阵进而，利用协方差矩阵及协方差矩阵计算得到第l个发射波束对应的协方差矩阵

需要说明的是，MIMO雷达的方向图函数p(γ)可表示为如下所示的公式(1)：

其中，R_T表示发射信号的协方差矩阵，a_T(γ)表示发射信号的导向矢量，d表示阵元间距，λ表示发射信号波长，N表示阵元个数。

则，对应的最小均方误差函数可表示为如下所示的公式(2)：

式中，p_d(γ_l)表示期望得到的方向图函数，L为γ角被划分的份数，α为比例因子。

定义如下所示的矩阵R′：

其中，H(k)是h(n)的傅里叶变换，即且H(k)为一个实序列，对所有k，H(k)是集合{0，1}中的元素。

容易发现，矩阵R′是半正定矩阵，则有如下关系：

h(n)＝h^*(M-n+1) 公式(4)

进一步的，定义如下所示的向量e(k)：

根据公式(3)和(5)，行向量e^H(k)R′中的元素可表示为：

这样，根据公式(6)，k点处的能量即可表示为如下所示的公式(7)：

令则根据公式(7)，有如下所示的公式(8)：

将公式(8)与公式(2)所示的MIMO雷达的最小均方误差函数进行比较，可以发现，由于向量e(k)与导向矢量a_T(γ)相似，因此公式(8)与公式(2)所示的MIMO雷达的最小均方误差函数相类似，这样一来，即可使用公式(3)所示的矩阵R′来代替发射信号协方差矩阵R_T。

综上，基于上述推导，可利用公式(3)所示的矩阵R′来计算MIMO雷达发射信号的协方差矩阵。

即，步骤4中，利用第l个发射波束对应的方位角范围计算得到X轴上M_x个阵元发射信号的协方差矩阵具体可以包括以下子步骤：

(4a1)计算得到方位角范围对应的余角范围为其中

(4a2)计算空间位置取时匹配的离散频率采样点k_xmin，以及空间位置取时匹配的离散频率采样点k_xmax。

其中，min(·)表示取最小值，max(·)表示取最大值，表示向下取整，表示向上取整。

一种具体的实现方式中，步骤4a2中，计算空间位置取时匹配的离散频率采样点k_xmin，以及空间位置取时匹配的离散频率采样点k_xmax，可以包括：

当时，利用第一预设公式计算得到离散频率采样点k_xmin；当时，利用第二预设公式计算得到离散频率采样点k_xmin；

以及，

当时，利用第一预设公式计算得到离散频率采样点k_xmax；当时，利用第二预设公式计算得到离散频率采样点k_xmax。

即，当(或)大于等于0时，将(或)代入第一预设公式计算得到匹配的离散频率采样点k_xmin(或k_xmax)；而兰(或)小于0时，将(或)代入第二预设公式计算得到匹配的离散频率采样点k_xmin(或k_xmax)。

(4a3)根据离散频率采样点k_xmin和离散频率采样点k_xmax，计算得到和

(4a3)令H_x(k)在和处取值为1，在处取值为0，进而对H_x(k)进行逆傅里叶变换得到并利用h_x(n)构造得到协方差矩阵

类似的，步骤4中，利用第l个发射波束对应的俯仰角范围计算得到Y轴上M_y个阵元发射信号的协方差矩阵具体可以包括以下子步骤：

(4b1)计算空间位置取时匹配的离散频率采样点k_ymin，以及空间位置取时匹配的离散频率采样点k_ymax。

具体的，步骤4b1中，计算空间位置取时匹配的离散频率采样点k_ymin，以及空间位置取时匹配的离散频率采样点k_ymax，可以包括：

当时，利用第三预设公式计算得到离散频率采样点k_ymin；当时，利用第四预设公式计算得到离散频率采样点k_ymin。

以及，

当时，利用第三预设公式计算得到离散频率采样点k_ymax；当时，利用第四预设公式计算得到离散频率采样点k_ymax。

即，当(或)大于等于0时，将(或)代入第三预设公式计算得到匹配的离散频率采样点k_ymin(或k_ymax)；而当(或)小于0时，将(或)代入四预设公式计算得到匹配的离散频率采样点k_ymin(或k_ymax)。

(4b2)根据离散频率采样点k_ymin和离散频率采样点k_ymax计算得到和

其中，min(·)表示取最小值，max(·)表示取最大值，表示向下取整，表示向上取整。

(4b3)令H_y(k)在和处取值为1，在处取值为0，进而对H_y(k)进行逆傅里叶变换得到并利用h_y(n)构造得到协方差矩阵

步骤5，令l加1，重复执行步骤3-步骤4，直至l＝L，得到全部L个发射波束中各发射波束对应的协方差矩阵，进而利用各发射波束对应的协方差矩阵以及K×I个发射导向矢量，计算得到MIMO雷达的方向图函数。

具体的，步骤5中，利用各发射波束对应的协方差矩阵以及K×I个发射导向矢量，计算得到MIMO雷达的方向图函数，包括以下子步骤：

(5a)对于K个俯仰角中的任一俯仰角θ_k和I个方位角中的任一方位角利用处的发射导向矢量以及各发射波束对应的协方差矩阵，计算处的方向图函数从而得到K×I个方向图函数。

其中，l∈{1，2，…，L}，上标H表示共轭转置。

具体的，方向图函数可通过如下所示的公式(9)来计算：

其中，公式(9)的推导过程如下：

已知方向图函数可使用MIMO雷达的发射信号表示为如下所示的公式(10)：

式中，S(n)表示发射信号，N为S(n)的信号长度。

又有，发射信号的协方差矩阵则公式(10)可变换为如下所示的公式(11)：

进一步的，MIMO雷达的方向图函数是由各发射波束对应的方向图函数叠加而成的，这样，根据公式(11)即可得到公式9。

(5b)利用K×I个方向图函数，构造得到MIMO雷达的方向图函数：

至此，即得到MIMO雷达的方向图函数，本发明实施例提供的基于FFT的平面阵MIMO雷达波形设计方法即结束。

本发明实施例提供的基于FFT的平面阵MIMO雷达波形设计方法，首先，建立MIMO雷达在笛卡尔坐标系中的几何模型，并分别按照固定间隔在二维均匀平面阵列的方位角范围及俯仰角范围内均匀抽取多个方位角和俯仰角，对于其中的任一方位角和任一俯仰角，计算得到对应的发射导向矢量；接着，对于每一个发射波束，分别在二维均匀平面阵列的方位角范围及俯仰角范围内随机抽取两个数值构成对应的方位角范围及俯仰角范围，并利用构造得到的方位角范围计算得到X轴上的协方差矩阵，利用构造得到的俯仰角范围计算得到Y轴上的协方差矩阵，再利用X轴上的协方差矩阵和Y轴上的协方差矩阵计算得到该发射波束对应的协方差矩阵；进而利用所得的全部协方差矩阵及全部发射导向矢量计算得到MIMO雷达的方向图函数。

相比于现有技术，本发明上述方案能够实现对平面阵MIMO雷达的波形设计，且运算量较小。具体来说，本发明方法的运算复杂度为O(Nlog(N))，而现有的迭代算法的运算复杂度为(其中复杂度前缀η通常取)，可见，本发明方法的运算复杂度低于现有的迭代算法，因此基于本发明方法设计平面阵MIMO雷达的发射波形，运算量将较小。

以下通过仿真实验对本发明上述效果作进一步验证说明：

(一)实验场景：

所设计的MIMO雷达为二维均匀平面阵列，且所述二维均匀平面阵列水平放置，X轴和Y轴分别包含16个阵元；MIMO雷达的发射信号波长c＝3.0×10⁸m/s，f_c＝3.0×10⁸Hz；Y轴上阵元的基波束的俯仰角范围按照0.5°间隔划分，L＝181，每个确定的俯仰角对应的X轴上阵元的方位角范围θ∈[45°，135°]。16个阵元在X轴和Y轴万同上的位置均为λ/2。

单波束仿真场景为：俯仰角的期望区域为[-10°，10°]，方位角的期望区域为[80°，100°]；

多波束仿真场景为：俯仰角的期望区域分别为[-45°，-25°]，[-10°，10°]，[15°，35°]，方位角的期望区域分别为[110°，130°]，[80°，100°]，[50°，70°]。

(二)仿真方法

为验证本发明采用的方法，分别进行单波束方向图设计和多波束方向图设计，以及进行MATLAB仿真分析

(三)仿真内容

仿真1，用本发明方法进行单波束方向图设计，仿真结果如图3和图4所示，图3为使用本发明方法得到的MIMO雷达俯仰角维单波束方向图，图4为使用本发明方法得到的MIMO雷达二维单波束方向图。

仿真2，用本发明方法进行多波束方向图设计，仿真结果如图5和图6所示，图5为使用本发明方法得到的MIMO雷达俯仰角维多波束方向图，图6为使用本发明方法得到的MIMO雷达二维多波束方向图。

(四)实验结果分析

由仿真结果图3、图4、图5和图6可以看出，使用本发明方法设计得到的单波束和多波束具有很好的效果，而且提高了对二维均匀平面阵列的适用性。

仿真实验表明，本发明的基于FFT方法的平面阵MIMO雷达波形设计方法将二维均匀阵列与波形设计相联合，可以检测到更多的目标特征信息，提高了雷达的目标识别能力及对二维均匀平面阵列的适用性。

本领域普通技术人员可以理解：实现上述方法实施例的全部或部分步骤可以通过程序指令相关的硬件来完成，前述的程序可以存储于一计算机可读取存储介质中，该程序在执行时，执行包括上述方法实施例的步骤；而前述的存储介质包括：ROM、RAM、磁碟或者光盘等各种可以存储程序代码的介质。

以上所述，仅为本发明的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明揭露的技术范围内，可轻易想到变化或替换，都应涵盖在本发明的保护范围之内。因此，本发明的保护范围应以所述权利要求的保护范围为准。