一种考虑状态约束的液压系统自适应控制方法与流程

本发明涉及一种控制方法，具体涉及一种考虑状态约束的液压系统自适应控制方法。
背景技术：
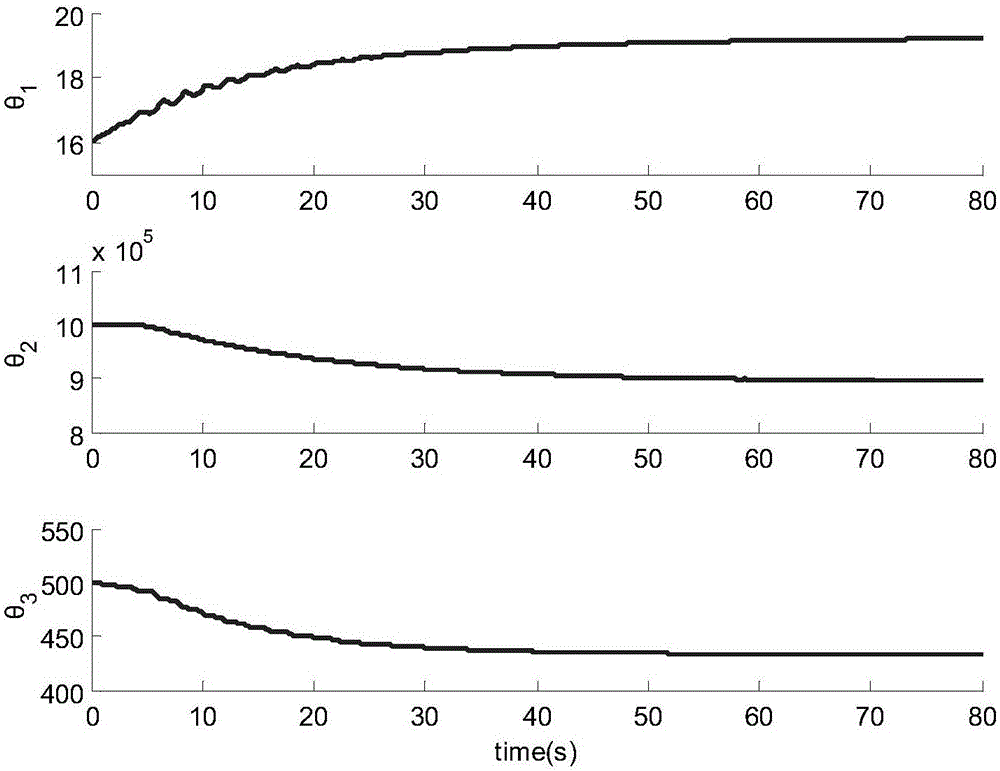
：液压系统由于输出力大、体积小等优点，在工业中得到了广泛的应用。然而，严重的非线性行为，如控制输入饱和，状态约束，阀门开度，非线性摩擦，模型的不确定性如负载变化、液压参数变化以及元件磨损引起的参数不确定性和包含外部干扰，泄漏等的不确定非线性，这些因素制约了高性能闭环控制器的发展。为了取得高精度跟踪性能，越来越多的研究人员设计非线性控制器以补偿液压伺服系统的非线性特性。如自适应鲁棒控制器、基于误差符号鲁棒积分的自适应控制器、基于扩张状态观测器的输出反馈控制器、滑膜控制器等，这些非线性控制被广泛用于液压伺服系统，提高了系统控制精度。同时系统中存在的控制输入饱和、时滞等，也吸引了众多注意力。此外，许多研究者也对系统状态约束问题展开了研究。但都没有考虑系统中扰动问题。实际上，一些系统常常受到状态约束的影响，如化学反应中的温度约束以及一些机械系统遭受物理故障时的速度或加速度约束。由于液压系统的高承载能力和高刚度性质，在环境和测量单元的相互作用的测试中，如果忽视输出状态约束问题，测试过程中过大的速度或加速度可能损坏测量设备。在测试和实验中，如果系统的初始条件不匹配，就有可能出现速度或加速度过大的情况。因此，本文针对此问题，开展基于速度和加速度约束的液压系统的运动跟踪控制研究，设计了一种考虑状态约束的液压系统自适应控制器。技术实现要素：本发明为解决电液伺服伺服系统中参数确定性、不确定非线性和加速度约束问题，进而提出一种考虑状态约束的液压系统自适应控制方法。本发明为解决上述问题采取的具体步骤如下：步骤1，建立双出杆液压缸位置伺服系统模型，根据牛顿第二定律，双出杆液压缸惯性负载的动力学模型方程为：my··=PLA-by·+f(t,y,y·)---(1)]]>式中：y为负载位移；m表示惯性负载；PL＝P1-P2是负载驱动压力；P1和P2分别为液压缸两腔压力；A为活塞杆有效工作面积；b代表粘性摩擦系数；f代表其他未建模干扰，比如非线性摩擦，外部干扰以及未建模动态。液压缸负载压力动态方程为：Vt4βeP·L=-Ay·-CtPL+QL---(2)]]>式中：Vt为液压缸两腔总有效容积；Ct为液压缸泄露系数；QL＝(Q1+Q2)/2为负载流量；Q1为液压缸供油流量；Q2为液压缸回油流量。QL为伺服阀阀芯位移xv的函数：QL=kqxvPs-sign(xv)PL---(3)]]>式中：为伺服阀的增益系数；Cd为伺服阀的流量系数；w为伺服阀的面积梯度；ρ为液压油的密度；Ps为供油压力；Pr为回油压力。sign(xv)为假设伺服阀阀芯位移正比于控制输入u，即xv＝kiu，其中ki>0是比例系数，u是控制输入电压。因此，等式(3)可以转化为QL=ktuPs-sign(u)PL---(5)]]>式中：kt＝kqki表示总的流量增益。定义状态变量那么整个系统可以写成如下状态空间形式：x·1=x2x·2=x3x·3=θ1gu-θ2x2-θ3x3-d(t)Δ(t)=1ktq(t)+CtAktf(t)+Vt4Aβektf·(t)---(6)]]>定义未知参数集θ＝[θ1,θ2,θ3]T，其中θ1＝4Aβekt/mVt，θ2＝(4A2βe+4βeCtB)/mVt，θ3＝(VtB+4βeCtm)/mVt，d(t)＝4AβektΔ(t)/mVt表示集中干扰。对于具体的实际应用系统，其大致信息是可以知道的。此外，系统的未建模动态和干扰总是有界的。因而，以下假设总是成立的：假设1：参数不确定性θ满足：θ∈Ωθ=Δ{θ:θmin≤θ≤θmax}---(7)]]>式中：θmin＝[θ1min,θ2min,θ3min]T和θmax＝[θ1max,θ2max,θ3max]T，它们都是已知的，此外θ1min>0,θ2min>0,θ3min>0。假设2：d(x,t)是有界的且其一阶导数也有界，即|d(x,t)|≤δ1,|d·(x,t)|≤δ2---(8)]]>式中：δ1和δ2已知。步骤2，设计考虑状态约束的液压系统自适应控制器的具体步骤如下：步骤2.1，带速率限制的投影自适应律结构令表示θ的估计，表示θ的估计误差，即定义一个投影函数式中：ζ∈Rp,Γ(t)∈Rp×p；和分别表示Ωθ的内部和边界；表示时的外单位法向量。参数估计过程中，预设合适的自适应速率。因而，定义一个饱和函数如下：satθ·M(ζ)=s0ζ,s0=1||ζ||≤θ·Mθ·M||ζ||,||ζ||>θ·M---(10)]]>式中：是一个预先设置的限制速率。下面的引理，总结了本文中将要用到的参数估计算法的结构特性。引理1：假设使用下面的投影型自适应律和预设的自适应限制速率更新估计参数θ^·=satθ·M(Projθ^(Γτ)),θ^(0)⊆Ωθ---(11)]]>式中：τ是自适应函数；Γ(t)＞0是连续可微的正对称自适应律矩阵。由此自适应律，可得以下性质：P1)参数估计值总在已知有界的Ωθ集内，即对于任意t，总有因而由假设1可得，P2)P3)参数变化律是一致有界的。即||θ^·(t)||≤θ·M,∀t]]>步骤2.2，设计干扰观测器。首先，把式(6)写成如下形式：x·1=x2x·2=x3x·3=θ^1gu-θ^2x2-θ^3x3-D(t)---(12)]]>式中：是一个广义干扰。由假设2和可知，D(x,t)也是有界且一阶导数有界的。由式(12)可以设计一个D(x,t)的干扰观测器e·0=v0+θ^1gu-θ^2x2-θ^3x3,e·1=v1=D^·,e·2=v2=D·^·v0=-λ0|e0-x3|2/3s(e0-x3)+e1v1=-λ1|e1-v0|1/2s(e1-v0)+e2v2=-λ2s(e2-v1)---(13)]]>式中：λi>0,(i＝0,1,2)为观测器系数；分别为D,的估计值。引理2：存在一个时间T1，当时间t大于时间常数T1时，式中：注1：理论上,总是能选择足够大的设计参数来保证任意小的时间段T1。本文取T1为零。步骤2.3，设计加速度控制器如下：步骤2.3.1，定义位置跟踪误差z1＝x1-x1d,z2＝x2-α1，式中：α1为第一个方程的虚拟控制律。定义如下的函数：V1＝k1z1arctan(z1)(14)式中：k1为正值常数。给定如下的稳定函数α1：α1＝x2d-v1arctan(z1)(15)式中：v1>0为控制器增益。因此稳定函数α1是有界的，即：|α1|＜πv1/2+|x2d|(16)此时函数V1的时间微分为：V·1=-W1+k1z2[arctan(z1)+z11+z12]---(17)]]>式中：W1定义为：W1=k1v1arctan(z1)[arctan(z1)+z11+z12]---(18)]]>由其构成可知，W1恒为正。因此由(17)可知，若z2＝0，则由(17)可知，定义的Lyapunov函数(14)保证了向第二方程传播的误差项是有界的，即：k1|arctan(z1)+z11+z12|≤k1|arctan(z1)|+k1|z11+z12|≤k1(π2+12)---(19)]]>步骤2.3.2，对于系统方程(6)的第二个方程，由于要确保速度输出满足约束，由z2＝x2-α1可知，已经约束了稳定函数α1，因此只要再确保z2在一个给定的范围(-L2,L2)内，即可约束状态x2。为此定义如下的BLF：V2=V1+12k2logL22L22-z22---(20)]]>式中：k2为正值常数。由式(20)可知，V2在开区间(-L2,L2)内关于z2是有效的Lyapunov函数。函数V2的时间微分为:V·2=V·1+k2z2z·2L22-z22=-W1+k1z2[arctan(z1)+z11+z12]+k2z2(x3-α·1)L22-z22---(21)]]>定义z3＝x3-α2，α2为第二步的虚拟控制律，设计如下：α2=α·1-v2z2-k1k2(L22-z22)[arctan(z1)+z11+z12]---(22)]]>式中：v2>0为控制器增益，且α·1=x3d-v1z·11+z12---(23)]]>由此则(21)可化为：V·2=-W2+k2z2z3L22-z22---(24)]]>式中：W2定义为W2=W1+k2v2z22L22-z22---(25)]]>由式(24)可知，若z3＝0，则就可以确保z2恒在(-L2,L2)范围内，即确保了x2有界，进而(23)有界，因此第二步虚拟控制律(22)有界，即α2有界。步骤2.3.3，对于系统第三个状态方程，约束系统的加速度输出x3，类似于第二步，已经约束了α2，只要再约束z3即可。为此，需要设计实际的控制输入u，以保证z3不侵犯预设的范围(-L3,L3)。为此定义如下的BLF函数：V3=V2+12k3logL32L32-z32---(26)]]>式中：k3为正值常数。因此V3在开区间(-L3,L3)内是关于z3有效的Lyapunov函数。函数V3的时间微分为：V·3=V·2+k3z3z·3L32-z32=-W2+k2z2z3L22-z22+k3z3[θ1gu-θ2x2-θ3x3-d(t)-α·2]L32-z32---(27)]]>式中：α·2=x·3d-v1z··11+z12+2v1z1z·12(1+z12)2-v2z·2+2k1k2z2z·2z11+z12+2k1k2z2z·2arctan(z1)-k1k22z·11+z12(L22-z22)[1-z121+z12]---(28)]]>基于干扰观测器(13)，可以获得因此，可设计如下控制器：u=1θ^1g[θ^2x2+θ^3x3D^(x,t)+α·2-k2k3L32-z32L22-z22z2-v3z3]---(29)]]>式中：v3>0为控制器增益。将控制器(29)带入(27)有：V·3=-W2-k3v3z32L32-z32=-W3---(30)]]>式中：W3定义为：W3=W2+k3v3z32L32-z32---(31)]]>由(31)可知，W3关于z,z＝[z1,z2,z3]T是正定的，因此由此确保了z3始终在范围(-L3,L3)内，由此也成功约束了系统加速度输出z3。由此可通过调整控制器参数约束系统的速度及加速度输出。步骤2.4，间接参数估计算法：假设系统干扰估计准。重写式(2)中第三个方程，可得到下式用于参数估计：y1=x·3+D^(t)=θ1gu-θ2x2-θ3x3---(32)]]>引入一个低通滤波器Hf，并把滤波器运用到式(32)中，可以得到y1f=Hf[x·3+D^(t)]=θ1guf-θ2x2f-θ3x3f---(33)]]>式中：uf,x2f分别表示输入为u，x2的滤波器Hf的输出。为进行参数估计，定义参数向量和回归函数：由式(28)可得线性回归模型定义预测输出误差式中：由式(35)可得预测误差模型：对于这种静态的线性回归模型，有多种不同的估计算法可以用来确定未知参数，本文使用一种具有指数遗忘因子和协方差预设的最小二乘估计算法。对于每一组的回归量和相应的未知参数向量，可以定义的自适应律矩阵：式中：Γ(0)＝ΓT(0)＞0；α≥0是遗忘因子；是协方差的预设时间；当λmin(Γ(t))＝ρl，ρl为Γ(t)的最小限值并满足0＜ρl＜ρ0，λmin(Γ(t))是Γ(t)的最小特征值，I是单位矩阵。此时自适应函数：式中：υ≥0是归一化因子，当υ＝0时，自适应函数为非标准型的自适应函数。但是，在含有遗忘因子的参数估计中，当回归器不是持续激励的，Γ(t)可能会无界。即λmax(Γ(t))→∞和导致估计器的饱和。为了防止这种情况发生，将式(37)修改为：式中：ρM是预设的Γ(t)的范数的上界，且λmax(Γ(t))≤ρM，0＜ρl＜ρ＜ρM。基于这种改进，可以保证ρlI＜Γ(t)＜ρMI。基于引理2，如果持续激励(PE)条件满足：则参数收敛到真值，即当t→∞时，基于以上定义的参数自适应律，可得到如下引理：引理3：由参数自适应律(11)，自适应函数(38)，式(39)以及预测误差模型(36)可得：ε∈L2(0,∞)∩L∞(0,∞),步骤2.5，验证系统稳定性：定理1：如果系统初值z(0)满足如下条件：z(0)∈Ωz0=Δ{|z2(0)|<L2,|z3(0)|<L3}---(41)]]>则控制器(29)具有如下结论：A、闭环控制器中所有信号都是有界的；且误差信号z2、z3满足如下不等式：z2≤L21-e-2V3(0)/k2z3≤L31-e-2V3(0)/k3---(42)]]>B、除结论A外，控制器还可获得渐近稳定性，即当t→∞时，z1→0。证明：由(30)可得，V3≤V3(0),且是不增的函数，因此可确保|z2(t)|<L2,|z3(t)|<L3。由此可推导出12k2logL22L22-z22≤V2≤V3≤V3(0)12k2logL32L32-z32≤V2≤V3≤V3(0)---(43)]]>因此可得不等式(42)。又V3有界，进而z有界，又系统位置指令、速度指令、加速度指令及加加速度指令均有界。进而可得系统状态x有界，又由不连续映射的参数估计可知，参数估计有界，据此可轻易证明闭环系统中所有信号均有界。由此证明了结论A。下面考虑结论B的证明。由(30),W3∈L2及V3∈L∞。此外，闭环系统所有信号均有界，很容易证明W3的时间微分也有界，即W3一致连续，由巴巴拉特引理可知当t→∞时有W3→0,此证明了结论B。因此控制器是收敛的，系统是稳定的。步骤3，调节基于控制律u的参数k1，k2，k3，λ0，λ1，λ2，v1，v2，v3，L2,L3,v，α，使系统满足控制性能指标。本发明的有益效果是：本发明针对电液伺服系统的特点，建立了双出杆系统模型；本发明设计的考虑状态约束的液压系统自适应控制器，对系统干扰和未知参数进行估计并用于控制器设计，能有效解决电机伺服系统的参数不确定性和不确定非线性问题；同时通过设计障碍李雅普诺夫函数，解决了系统加速度约束问题；本发明简化了控制器设计，实验结果表明了其有效性。下面结合说明书附图对本发明做进一步说明。附图说明图1是本发明方法流程示意图。图2是ACSC控制器作用下参数估计曲线示意图。图3是指令信号x1d及两个控制器的跟踪误差示意图。图4是d(t)的估计曲线示意图。图5是两种控制器作用下的速度状态x2输出曲线示意图。图6两种控制器作用下的加速度状态x3输出曲线示意图。具体实施方式结合图1，本实施方式所述一种考虑状态约束的液压系统自适应控制方法的具体步骤如下：步骤1，建立双出杆液压缸位置伺服系统模型，根据牛顿第二定律，双出杆液压缸惯性负载的动力学模型方程为：my··=PLA-by·+f(t,y,y·)---(1)]]>式中：y为负载位移；m表示惯性负载；PL＝P1-P2是负载驱动压力；P1和P2分别为液压缸两腔压力；A为活塞杆有效工作面积；b代表粘性摩擦系数；f代表其他未建模干扰，比如非线性摩擦，外部干扰以及未建模动态。液压缸负载压力动态方程为：Vt4βeP·L=-Ay·-CtPL+QL---(2)]]>式中：Vt为液压缸两腔总有效容积；Ct为液压缸泄露系数；QL＝(Q1+Q2)/2为负载流量；Q1为液压缸供油流量；Q2为液压缸回油流量。QL为伺服阀阀芯位移xv的函数：QL=kqxvPs-sign(xv)PL---(3)]]>式中：为伺服阀的增益系数；Cd为伺服阀的流量系数；w为伺服阀的面积梯度；ρ为液压油的密度；Ps为供油压力；Pr为回油压力。sign(xv)为假设伺服阀阀芯位移正比于控制输入u，即xv＝kiu，其中ki>0是比例系数，u是控制输入电压。因此，等式(3)可以转化为QL=ktuPs-sign(u)PL---(5)]]>式中：kt＝kqki表示总的流量增益。定义状态变量那么整个系统可以写成如下状态空间形式：x·1=x2x·2=x3x·3=θ1gu-θ2x2-θ3x3-d(t)Δ(t)=1ktq(t)+CtAktf(t)+Vt4Aβektf·(t)---(6)]]>定义未知参数集θ＝[θ1,θ2,θ3]T，其中θ1＝4Aβekt/mVt，θ2＝(4A2βe+4βeCtB)/mVt，θ3＝(VtB+4βeCtm)/mVt，d(t)＝4AβektΔ(t)/mVt表示集中干扰。对于具体的实际应用系统，其大致信息是可以知道的。此外，系统的未建模动态和干扰总是有界的。因而，以下假设总是成立的：假设1：参数不确定性θ满足：θ∈Ωθ=Δ{θ:θmin≤θ≤θmax}---(7)]]>式中：θmin＝[θ1min,θ2min,θ3min]T和θmax＝[θ1max,θ2max,θ3max]T，它们都是已知的，此外θ1min>0,θ2min>0,θ3min>0。假设2：d(x,t)是有界的且其一阶导数也有界，即|d(x,t)|≤δ1,|d·(x,t)|≤δ2---(8)]]>式中：δ1和δ2已知。步骤2，设计考虑状态约束的液压系统自适应控制器的具体步骤如下：步骤2.1，带速率限制的投影自适应律结构令表示θ的估计，表示θ的估计误差，即定义一个投影函数式中：ζ∈Rp,Γ(t)∈Rp×p；和分别表示Ωθ的内部和边界；表示时的外单位法向量。参数估计过程中，预设合适的自适应速率。因而，定义一个饱和函数如下：satθ·M(ζ)=s0ζ,s0=1||ζ||≤θ·Mθ·M||ζ||,||ζ||>θ·M---(10)]]>式中：是一个预先设置的限制速率。下面的引理，总结了本文中将要用到的参数估计算法的结构特性。引理1：假设使用下面的投影型自适应律和预设的自适应限制速率更新估计参数θ^·=satθ·M(Projθ^(Γτ)),θ^(0)⊆Ωθ---(11)]]>式中：τ是自适应函数；Γ(t)＞0是连续可微的正对称自适应律矩阵。由此自适应律，可得以下性质：P1)参数估计值总在已知有界的Ωθ集内，即对于任意t，总有因而由假设1可得，P2)P3)参数变化律是一致有界的。即||θ^·(t)||≤θ·M,∀t]]>步骤2.2，设计干扰观测器。首先，把式(6)写成如下形式：x·1=x2x·2=x3x·3=θ^1gu-θ^2x2-θ^3x3-D(t)---(12)]]>式中：是一个广义干扰。由假设2和可知，D(x,t)也是有界且一阶导数有界的。由式(12)可以设计一个D(x,t)的干扰观测器e·0=v0+θ^1gu-θ^2x2-θ^3x3,e·1=v1=D^·,e·2=v2=D·^·v0=-λ0|e0-x3|2/3s(e0-x3)+e1v1=-λ1|e1-v0|1/2s(e1-v0)+e2v2=-λ2s(e2-v1)---(13)]]>式中：λi>0,(i＝0,1,2)为观测器系数；分别为D,的估计值。引理2：存在一个时间T1，当时间t大于时间常数T1时，式中：注1：理论上,总是能选择足够大的设计参数来保证任意小的时间段T1。本文取T1为零。步骤2.3，设计加速度控制器如下：步骤2.3.1，定义位置跟踪误差z1＝x1-x1d,z2＝x2-α1，式中：α1为第一个方程的虚拟控制律。定义如下的函数：V1＝k1z1arctan(z1)(14)式中：k1为正值常数。给定如下的稳定函数α1：α1＝x2d-v1arctan(z1)(15)式中：v1>0为控制器增益。因此稳定函数α1是有界的，即：|α1|＜πv1/2+|x2d|(16)此时函数V1的时间微分为：V·1=-W1+k1z2[arctan(z1)+z11+z12]---(17)]]>式中：W1定义为：W1=k1v1arctan(z1)[arctan(z1)+z11+z12]---(18)]]>由其构成可知，W1恒为正。因此由(17)可知，若z2＝0，则由(17)可知，定义的Lyapunov函数(14)保证了向第二方程传播的误差项是有界的，即：k1|arctan(z1)+z11+z12|≤k1|arctan(z1)|+k1|z11+z12|≤k1(π2+12)---(19)]]>步骤2.3.2，对于系统方程(6)的第二个方程，由于要确保速度输出满足约束，由z2＝x2-α1可知，已经约束了稳定函数α1，因此只要再确保z2在一个给定的范围(-L2,L2)内，即可约束状态x2。为此定义如下的BLF：V2=V1+12k2logL22L22-z22---(20)]]>式中：k2为正值常数。由式(20)可知，V2在开区间(-L2,L2)内关于z2是有效的Lyapunov函数。函数V2的时间微分为:V·2=V·1+k2z2z·2L22-z22=-W1+k1z2[arctan(z1)+z11+z12]+k2z2(x3-α·1)L22-z22---(21)]]>定义z3＝x3-α2，α2为第二步的虚拟控制律，设计如下：α2=α·1-v2z2-k1k2(L22-z22)[arctan(z1)+z11+z12]---(22)]]>式中：v2>0为控制器增益，且α·1=x3d-v1z·11+z12---(23)]]>由此则(21)可化为：V·2=-W2+k2z2z3L22-z22---(24)]]>式中：W2定义为W2=W1+k2v2z22L22-z22---(25)]]>由式(24)可知，若z3＝0，则就可以确保z2恒在(-L2,L2)范围内，即确保了x2有界，进而(23)有界，因此第二步虚拟控制律(22)有界，即α2有界。步骤2.3.3，对于系统第三个状态方程，约束系统的加速度输出x3，类似于第二步，已经约束了α2，只要再约束z3即可。为此，需要设计实际的控制输入u，以保证z3不侵犯预设的范围(-L3,L3)。为此定义如下的BLF函数：V3=V2+12k3logL32L32-z32---(26)]]>式中：k3为正值常数。因此V3在开区间(-L3,L3)内是关于z3有效的Lyapunov函数。函数V3的时间微分为：V·3=V·2+k3z3z·3L32-z32=-W2+k2z2z3L22-z22+k3z3[θ1gu-θ2x2-θ3x3-d(t)-α·2]L32-z32---(27)]]>式中：α·2=x·3d-v1z··11+z12+2v1z1z·12(1+z12)2-v2z·2+2k1k2z2z·2z11+z12+2k1k2z2z·2arctan(z1)-k1k22z·11+z12(L22-z22)[1-z121+z12]---(28)]]>基于干扰观测器(13)，可以获得因此，可设计如下控制器：u=1θ^1g[θ^2x2+θ^3x3D^(x,t)+α·2-k2k3L32-z32L22-z22z2-v3z3]---(29)]]>式中：v3>0为控制器增益。将控制器(29)带入(27)有：V·3=-W2-k3v3z32L32-z32=-W3---(30)]]>式中：W3定义为：W3=W2+k3v3z32L32-z32---(31)]]>由(31)可知，W3关于z,z＝[z1,z2,z3]T是正定的，因此由此确保了z3始终在范围(-L3,L3)内，由此也成功约束了系统加速度输出z3。由此可通过调整控制器参数约束系统的速度及加速度输出。步骤2.4，间接参数估计算法：假设系统干扰估计准。重写式(2)中第三个方程，可得到下式用于参数估计：y1=x·3+D^(t)=θlgu-θ2x2-θ3x3---(32)]]>引入一个低通滤波器Hf，并把滤波器运用到式(32)中，可以得到y1f=Hf[x·3+D^(t)]=θlguf-θ2x2f-θ3x3f---(33)]]>式中：uf,x2f分别表示输入为u，x2的滤波器Hf的输出。为进行参数估计，定义参数向量和回归函数：由式(28)可得线性回归模型定义预测输出误差式中：由式(35)可得预测误差模型：对于这种静态的线性回归模型，有多种不同的估计算法可以用来确定未知参数，本文使用一种具有指数遗忘因子和协方差预设的最小二乘估计算法。对于每一组的回归量和相应的未知参数向量，可以定义的自适应律矩阵：式中：Γ(0)＝ΓT(0)＞0；α≥0是遗忘因子；是协方差的预设时间；当λmin(Γ(t))＝ρl，ρl为Γ(t)的最小限值并满足0＜ρl＜ρ0，λmin(Γ(t))是Γ(t)的最小特征值，I是单位矩阵。此时自适应函数：式中：υ≥0是归一化因子，当υ＝0时，自适应函数为非标准型的自适应函数。但是，在含有遗忘因子的参数估计中，当回归器不是持续激励的，Γ(t)可能会无界。即λmax(Γ(t))→∞和导致估计器的饱和。为了防止这种情况发生，将式(37)修改为：式中：ρM是预设的Γ(t)的范数的上界，且λmax(Γ(t))≤ρM，0＜ρl＜ρ＜ρM。基于这种改进，可以保证ρlI＜Γ(t)＜ρMI。基于引理2，如果持续激励(PE)条件满足：则参数收敛到真值，即当t→∞时，基于以上定义的参数自适应律，可得到如下引理：引理3：由参数自适应律(11)，自适应函数(38)，式(39)以及预测误差模型(36)可得：ε∈L2(0,∞)∩L∞(0,∞),步骤2.5，验证系统稳定性：定理1：如果系统初值z(0)满足如下条件：z(0)∈Ωz0=Δ{|z2(0)|<L2,|z3(0)|<L3}---(41)]]>则控制器(29)具有如下结论：A、闭环控制器中所有信号都是有界的；且误差信号z2、z3满足如下不等式：z2≤L21-e-2V3(0)/k2z3≤L31-e-2V3(0)/k3---(42)]]>B、除结论A外，控制器还可获得渐近稳定性，即当t→∞时，z1→0。证明：由(30)可得，V3≤V3(0),且是不增的函数，因此可确保|z2(t)|<L2,|z3(t)|<L3。由此可推导出12k2logL22L22-z22≤V2≤V3≤V3(0)12k2logL32L32-z32≤V2≤V3≤V3(0)---(43)]]>因此可得不等式(42)。又V3有界，进而z有界，又系统位置指令、速度指令、加速度指令及加加速度指令均有界。进而可得系统状态x有界，又由不连续映射的参数估计可知，参数估计有界，据此可轻易证明闭环系统中所有信号均有界。由此证明了结论A。下面考虑结论B的证明。由(30),W3∈L2及V3∈L∞。此外，闭环系统所有信号均有界，很容易证明W3的时间微分也有界，即W3一致连续，由巴巴拉特引理可知当t→∞时有W3→0,此证明了结论B。因此控制器是收敛的，系统是稳定的。步骤3，调节基于控制律u的参数k1，k2，k3，λ0，λ1，λ2，v1，v2，v3，L2,L3,v，α，使系统满足控制性能指标。实施例：本文提出的考虑状态约束的液压系统自适应控制器(ACSC)。系统参数为：m＝30kg，A＝9.05×10-4m2，Vt＝7.96×10-5m3，Ps＝10Mpa，Pr＝0.08Mpa。选取参数不确定范围为θmin＝[1,1×105,10]T，θmax＝[200,1×107,2000]T，给定参数估计初值为控制器设计参数v1＝800，v2＝500，v3＝300，k1＝5，k2＝1，k3＝0.1，L2＝0.12，L3＝2.5，λ0＝50，λ1＝600，λ2＝800，α＝20，ν＝1.5。位置角度输入信号x1d＝10arctan(sin(0.4πt))[1-exp(-t)]+5(mm)。为了验证本文提出控制策略的有效性，引入PI控制器做对比，PI控制器参数为kp＝1500,ki＝500。控制律作用效果：图2是ACSC控制器作用下参数估计曲线。图3是指令信号x1d及两个控制器的跟踪误差。图4是d(t)的估计曲线。图5是两种控制器作用下的速度状态x2输出曲线。图6是两种控制器作用下的加速度状态x3输出曲线。由上图可知，本发明提出的算法在实验环境下能够准确的估计出干扰和系统参数。相比PI控制器，本发明设计的控制器能够取得更好的控制精度和加速度约束。研究结果表明在参数不确定性和不确定非线性性影响下，本文提出的方法能够取得良好的性能。当前第1页1 2 3