一种基于直接自适应律的固定时间反步控制方法

1.本发明属于非线性系统的控制技术领域。


背景技术：

2.自适应反步控制方法已被广泛应用于机器人控制系统、飞行器控制系统以及工业伺服控制系统等。关于自适应反步控制方法的具体设计过程可以参考中国发明专利zl201410165505.3、zl201710219083.7以及zl201810942812.6。值得指出的是，传统的自适应反步控制方法存在两个缺陷：
3.一是传统控制方法下系统收敛速度较慢，通常需要较长的时间，系统状态才能收敛到原点附近；
4.二是传统控制方法只针对参数化不确定性系统，对于非参数化不确定性系统并不适用。
5.而对于一个实际系统，设计者通常希望系统响应速度尽可能快。并且，由于系统的不确定性往往是由一些非参数化非线性函数造成的，例如系统未建模动态，外部时变扰动等。因此，这两个因素将极大的限制传统自适应反步控制方法在实际系统中的应用。
6.综上所述，如何能设计出一种既能够直接处理系统非参数化不确定性，还能够实现系统快速响应的自适应反步控制方法是一个关键问题。


技术实现要素：

7.本发明是为了解决传统的自适应反步控制方法不仅不适用非参数话不确定性系统，而且还会导致系统收敛速度慢的问题，现提供一种基于直接自适应律的固定时间反步控制方法。
8.一种基于直接自适应律的固定时间反步控制方法，所述固定时间反步控制方法具体为：
9.建立二维非线性系统的状态空间模型，所述二维非线性系统中具有两个状态变量x1和x2、一个控制输入信号u以及一个给定的目标信号yd，
10.利用直接自适应律的反步控制器调整控制输入信号u，
11.将调整后的u输入至二维非线性系统中，使二维非线性系统的输出信号y在固定时间内能够跟踪给定目标信号yd，实现对二维非线性系统的反步控制；
12.上述直接自适应律的反步控制器表达式为：
[0013][0014]
其中，z1和z2为二维非线性系统的两个跟踪误差，且z1＝x
1-yd，z2＝x
2-α1，
[0015]
α1为虚拟控制函数，表达式为：
[0016]
s(
·
)为sigmod函数，
[0017]
和分别为h1和h2的估计值，
[0018]
和的一阶导表达式分别为：
[0019][0020]
e1＝ω
1-z1，e2＝ω
2-z2，
[0021]
ω1和ω2分别为z1和z2的估计值，和分别为ω1和ω2的一阶导数，
[0022]
d1(t)和d2(t)分别为二维非线性系统中分别作用于第一维度和第二维度的外部扰动项，
[0023]
ψ1(x1)和ψ2(x1,x2)分别为二维非线性系统中分别作用于第一维度和第二维度的未知非线性项，
[0024]
f1(x1)和f2(x1,x2)分别为二维非线性系统中分别作用于第一维度和第二维度的已知非线性项，
[0025]
b1和b2分别为二维非线性系统中分别作用于第一维度和第二维度的控制方向系数，
[0026]
k1和k2分别为ε1和ε2中sigmod函数的系数，l1和l2分别为ε1和ε2中的误差变量系数，μ1和μ2分别为和中sigmod函数的系数，σ1和σ2分别为和中ε1和ε2的系数，γ1和γ2分别为和中sigmod函数的系数，β1和β2分别为和中e1和e2的系数，k1、k2、l1、l2、μ1、μ2、σ1、σ2、γ1、γ2、β1和β2均属于直接自适应律的反步控制器中的参数且取值均大于0。
[0027]
进一步的，上述状态空间模型表达式为：
[0028][0029]
其中，和分别为x1和x2的一阶导数。
[0030]
进一步的，上述状态空间模型存在唯一解，
[0031]
f1(x1)、f2(x1,x2)、ψ1(x1)、ψ2(x1,x2)、d1(t)和d2(t)，以及其一阶导数均有界，
[0032]
状态空间模型给定的目标信号yd及其一阶导数均有界。
[0033]
进一步的，上述直接自适应律的反步控制器的获得方法为：
[0034]
根据状态空间模型定义二维非线性系统的两个误差变量z1和z2，并利用z1和z2设计李雅普诺夫函数v，对李雅普诺夫函数v求导，最后根据李雅普诺夫函数v的一阶导数和实用性固定时间有界李雅普诺夫稳定性判据获得直接自适应律的反步控制器。
[0035]
进一步的，上述李雅普诺夫函数v的表达式如下：
[0036][0037]
进一步的，上述李雅普诺夫函数v的一阶导数v的表达式如下：
[0038]
[0039]
进一步的，上述sigmod函数s(
·
)的表达式为：
[0040][0041]
其中，q为sigmod函数的变量，λ为大于0的常数。
[0042]
进一步的，上述实用性固定时间有界李雅普诺夫稳定性判据为：
[0043]
设有系统存在参数α、β、θ、m、p以及正定函数v(x)，其中α、β、θ和m均为大于0的常数，0＜p＜1，v[x(0)]≤m，
[0044]
使得：
[0045][0046]
则系统的解是实用性固定时间稳定的，并会在固定时间t内收敛到以下集合：
[0047][0048]
其中，ρ∈(0,1)，
[0049]
t的表达式为：
[0050][0051]
其中，r1＝(α/β)2，r2＝[θ/(α-αρ)]2，r1≥r2。
[0052]
进一步的，上述系统的表达式如下：
[0053][0054]
其中，x为系统状态变量且x∈rn，rn表示n维实数集，f
*
(
·
)为的非线性函数，f
*
(
·
):r
+
×rn
→rn
，r
+
为正实数集，x初始取值为0时x(0)＝x0，t为时间。
[0055]
本发明所述的一种基于直接自适应律的固定时间反步控制方法的有益效果如下：
[0056]
本发明提出了一种基于直接自适应律的固定时间反步控制方法，该固定时间反步控制方法利用直接自适应律的反步控制器调整控制输入信号，使系统跟踪误差在固定时间内收敛到原点附近较小的邻域内，然后利用调整后的控制输入信号输入至二维非线性系统中，使系统输出信号在固定时间内能够跟踪给定目标信号。本方法不仅收敛速度快且能够直接处理系统非参数化不确定性系统。
附图说明
[0057]
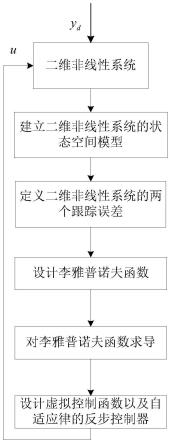
图1为具体实施方式一所述一种基于直接自适应律的固定时间反步控制方法的流程图；
[0058]
图2为二维非线性系统的跟踪性能曲线图；
[0059]
图3为二维非线性系统的未知函数h1及其估计值的曲线图；
[0060]
图4为二维非线性系统的未知函数h2及其估计值的曲线图；
[0061]
图5为二维非线性系统的控制输入信号响应曲线图。
具体实施方式
[0062]
下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有作出创造性劳动的前提下所获得的所有其它实施例，都属于本发明保护的范围。需要说明的是，在不冲突的情况下，本发明中的实施例及实施例中的特征可以相互组合。
[0063]
具体实施方式一：参照图1至5具体说明本实施方式，本实施方式所述的一种基于直接自适应律的固定时间反步控制方法，所述固定时间反步控制方法包括以下步骤：
[0064]
步骤一：建立二维非线性系统的状态空间模型，所述二维非线性系统中具有两个状态变量x1和x2、一个控制输入信号u以及一个给定的目标信号yd。
[0065]
上述状态空间模型表达式为：
[0066][0067]
其中，和分别为x1和x2的一阶导数，b1和b2分别为二维非线性系统中分别作用于第一维度和第二维度的控制方向系数，f1(x1)和f2(x1,x2)分别为二维非线性系统中分别作用于第一维度和第二维度的已知非线性项，ψ1(x1)和ψ2(x1,x2)分别为二维非线性系统中分别作用于第一维度和第二维度的未知非线性项，d1(t)和d2(t)分别为二维非线性系统中分别作用于第一维度和第二维度的外部扰动项，y为二维非线性系统的输出信号。
[0068]
上述状态空间模型存在唯一解，f1(x1)、f2(x1,x2)、ψ1(x1)、ψ2(x1,x2)、d1(t)和d2(t)，以及其一阶导数均有界，状态空间模型给定的目标信号yd及其一阶导数均有界。f1(x1)、f2(x1,x2)、ψ1(x1)和ψ2(x1,x2)均为非线性光滑函数。
[0069]
步骤二：根据状态空间模型定义二维非线性系统的两个跟踪误差z1和z2，表达式如下：
[0070][0071]
其中，α1为虚拟控制函数，该函数需要后续设计。
[0072]
步骤三：利用z1和z2设计李雅普诺夫函数v：
[0073][0074]
步骤四：对李雅普诺夫函数v求导，获得李雅普诺夫函数v的一阶导数
[0075][0076]
其中，未知函数h1和h2的表达式如下：
[0077][0078]
为yd的一阶导数，为α1的一阶导数。
[0079]
步骤五：根据李雅普诺夫函数的一阶导数和实用性固定时间有界李雅普诺夫稳定性判据设计虚拟控制函数α1以及直接自适应律的反步控制器。
[0080]
虚拟控制函数α1的表达式如下：
[0081][0082]
直接自适应律的反步控制器的表达式如下：
[0083][0084]
由于直接自适应律的反步控制器用于调整控制输入信号，进而使得二维非线性系统的跟踪误差在固定时间内收敛到原点附近较小的邻域内，因此直接自适应律的反步控制器的输出为二维非线性系统的控制输入信号u。
[0085]
上述虚拟控制函数α1以及控制输入信号u的表达式中存在未知函数h1和h2的估计值和设计和的一阶导为：
[0086][0087]
其中，s(
·
)为sigmod函数，表达式为：
[0088][0089]
其中，q为sigmod函数的变量，λ为大于0的常数。
[0090][0091]
e1＝ω
1-z1，e2＝ω
2-z2，
[0092]
ω1和ω2分别为z1和z2的估计值，和分别为ω1和ω2的一阶导数，
[0093]
以上k1、k2、l1、l2、μ1、μ2、σ1、σ2、γ1、γ2、β1和β2均属于直接自适应律的反步控制器中的参数且取值均大于0，具体的，k1和k2分别为ε1和ε2中sigmod函数的系数，l1和l2分别为ε1和ε2中的误差变量系数，μ1和μ2分别为和中sigmod函数的系数，σ1和σ2分别为和中ε1和ε2的系数，γ1和γ2分别为和中sigmod函数的系数，β1和β2分别为和中e1和e2的系数。
[0094]
至此，完成了直接自适应律的反步控制器对控制输入信号u的调整，将调整后的u输入至二维非线性系统中，使系统输出信号y在固定时间内能够跟踪给定目标信号yd，实现对二维非线性系统的反步控制。
[0095]
本实施方式利用直接自适应律的反步控制器调整控制输入信号，使系统跟踪误差在固定时间内收敛到原点附近较小的邻域内，然后利用调整后的控制输入信号输入至二维非线性系统中，使系统输出信号在固定时间内能够跟踪给定目标信号。本方法不仅收敛速度快且能够直接处理系统非参数化不确定性系统。
[0096]
本实施方式在具体应用时的一种实施例中，参数给定如下：
[0097]
状态变量x1和x2的初始取值分别为x1(0)＝0，x2(0)＝0。控制方向系数的取值分别为b1＝1.5，b2＝2。已知非线性项f1(x1)和f2(x1,x2)分别为f1(x1)＝2x
1 sinx1，f2(x1,x2)＝
3x1x2。未知非线性项ψ1(x1)和ψ2(x1,x2)分别为ψ1(x1)＝0.5x1，ψ2(x1,x2)＝10x2sinx1。外部扰动项d1(t)和d2(t)取值分别为0.1和0.2。给定的目标信号yd的取值为1.85。直接自适应律的反步控制器的参数分别为：k1＝2、k2＝20、l1＝2、l2＝25、γ1＝100、γ2＝100、β1＝50、β2＝50、μ1＝20、μ2＝80、σ1＝50、σ2＝80、λ＝20。系统采样间隔时间为0.002秒。
[0098]
举例说明，本实施方式可应用于电机系统中，两个状态变量x1和x2分别为转角和转速，而输出为电机系统转角。
[0099]
本实施方式所述的自适应律的反步控制器能够使系统跟踪误差在固定时间内收敛到原点附近较小的邻域内，其原理如下：
[0100]
考虑李雅普诺夫函数i＝1,2，带入e1＝ω
1-z1和e2＝ω
2-z2，并结合和的表达式可得：
[0101][0102]
其中，为常数项、取值大于零，δi为符号函数sgn(
·
)与sigmod函数的误差、且δi≤1，为的上界且有
[0103]
进一步设：
[0104][0105]
其中，
[0106]
将(2)式代入(1)式，整理可得：
[0107][0108]
其中，
[0109]
由实用性固定时间李雅普诺夫稳定性判据可得：
[0110][0111]
其中，ρ∈(0,1)。
[0112]
设到达时间tf的表达式如下：
[0113][0114]
其中，
[0115]
令可得：
[0116][0117]
其中，为滤波器估计误差上界，
[0118]
则由公式(6)可得：
[0119][0120]
其中
[0121]
将上述公式(7)带入到和中，可得：
[0122][0123]
设以及可得：
[0124][0125]
其中，ηi、ζi和均为常数且取值大于0。
[0126]
由实用性固定时间李雅普诺夫稳定性判据可得：
[0127][0128]
定义其到达时间
[0129][0130]
其中，
[0131]
可得：
[0132][0133]
设那么将虚拟控制函数α1以及控制输入信号u带入李雅普诺夫函数的一阶导数中可得：
[0134][0135]
进一步有：
[0136][0137]
其中，将公式(14)带入到公式(13)中，可得：
[0138][0139]
其中，
[0140]
由实用性固定时间李雅普诺夫稳定性判据可得：
[0141][0142]
定义到达时间tz为：
[0143][0144]
其中，r1＝(a/b)2，r2＝[c/(a-aρ)]2，r1≥r2，v[z(0)]≤mz。
[0145]
由公式(16)和(17)能够表明二维非线性系统的输出信号y能够在固定时间tz内跟踪给定目标信号yd。
[0146]
实用性固定时间李雅普诺夫稳定性判据就是：
[0147]
对于如下所示的系统：
[0148]
状态变量x∈rn，f
*
(
·
):r
+
×rn
→rn
为系统非线性函数。
[0149]
存在常数α,β,θ,m＞0、0＜p＜1以及正定函数v(x)，并且v[x(0)]≤m，使得：
[0150][0151]
则有公式(18)所示系统的解是实用性固定时间稳定的，并会在固定时间t内收敛到以下集合：
[0152][0153]
其中，ρ∈(0,1)，且到达时间t定义为：
[0154][0155]
其中，r1＝(α/β)2，r2＝[θ/(α-αρ)]2，r1≥r2。
[0156]
上述实用性固定时间李雅普诺夫稳定性判据的证明过程如下：
[0157]
当βv≥αv
p
时，即v≥(α/β)
1/(1-p)
，可得：
[0158][0159]
那么由公式(21)可得：
[0160][0161]
令r1＝(α/β)
1/(1-p)
、v[x(0)]≤m、θ/β≤r1≤m，则有：
[0162][0163]
当βv＜αv
p
时，即v＜r1,t＞t1，可得：
[0164][0165]
进一步的，令r2＝[θ/(α-αρ)]
1/p
、r2≤v≤r1，可得：
[0166][0167]
其中，t2＝{t|v[x(t)]＝r2}。
[0168]
根据公式(25)可得：
[0169][0170]
其中，δt＝t
2-t1。
[0171]
由公式(26)可得：
[0172][0173]
由公式(23)和公式(27)可得到达时间t满足：
[0174][0175]
上述公式(27)和(28)表明当时间t＞t时，系统的解会收敛到集合{x(t)|v[x(t)]≤r2}中。
[0176]
虽然在本文中参照了特定的实施方式来描述本发明，但是应该理解的是，这些实施例仅仅是本发明的原理和应用的示例。因此应该理解的是，可以对示例性的实施例进行许多修改，并且可以设计出其他的布置，只要不偏离所附权利要求所限定的本发明的精神和范围。应该理解的是，可以通过不同于原始权利要求所描述的方式来结合不同的从属权利要求和本文中所述的特征。还可以理解的是，结合单独实施例所描述的特征可以使用在其它所述实施例中。