基于非结构曲边网格的三维无粘低速绕流的数值模拟方法与流程

本发明属于三维流体力学数值求解技术领域，涉及一种基于非结构曲边网格的三维无粘低速绕流的数值模拟方法。

背景技术：

计算流体力学(简称cfd)一直以来在汽车制造、土木工程、环境工程、船舶工业以及航空工业等领域有着广泛的应用，其有助于解释、理解理论和实验的结果，是流体力学分析不可缺少的方法。前期由于计算机水平的限制，cfd的实际求解仅限于二维流动，而大部分的真实流动世界主要是三维的。随着计算机水平的发展，今天的cfd已经可以大量求解三维流场，虽然仍需要大量的人力和计算机资源，但是这种求解方法在工业设备中已得到广泛使用。

随着cfd的发展，相应的数值算法在cfd中的应用也随之发展起来，如有限差分、有限体积和有限元法等。随着工业技术的进步，流体动力学对数值算法的精度提出了更高的要求，因此需要高精度的数值模拟方法。间断galerkin有限元法由于其易于实现高阶精度、灵活处理间断问题、适用于非结构网格、有利于实现并行算法，因此有很好的应用前景和工程实用价值。然而间断galerkin有限元法的高阶精度实现依赖于边界的精度，这包括算法的精度和模型空间离散的精度，因此需要研究物面边界的空间离散，特别是复杂结构的边界拟合。虽然非结构网格的应用能够更好的拟合复杂结构边界，但是非结构网格也难以精确拟合曲面物面。模型空间离散的误差限制了边界的精度，从而制约了高精度算法的应用。

技术实现要素：

针对上述存在问题或不足，为解决空间离散误差导致数值算法精度低的问题；本发明提供了一种基于非结构曲边网格的三维无粘低速绕流的数值模拟方法，以非结构曲边网格来精确拟合曲面物面，在此基础上开发相应的高精度数值模拟方法。

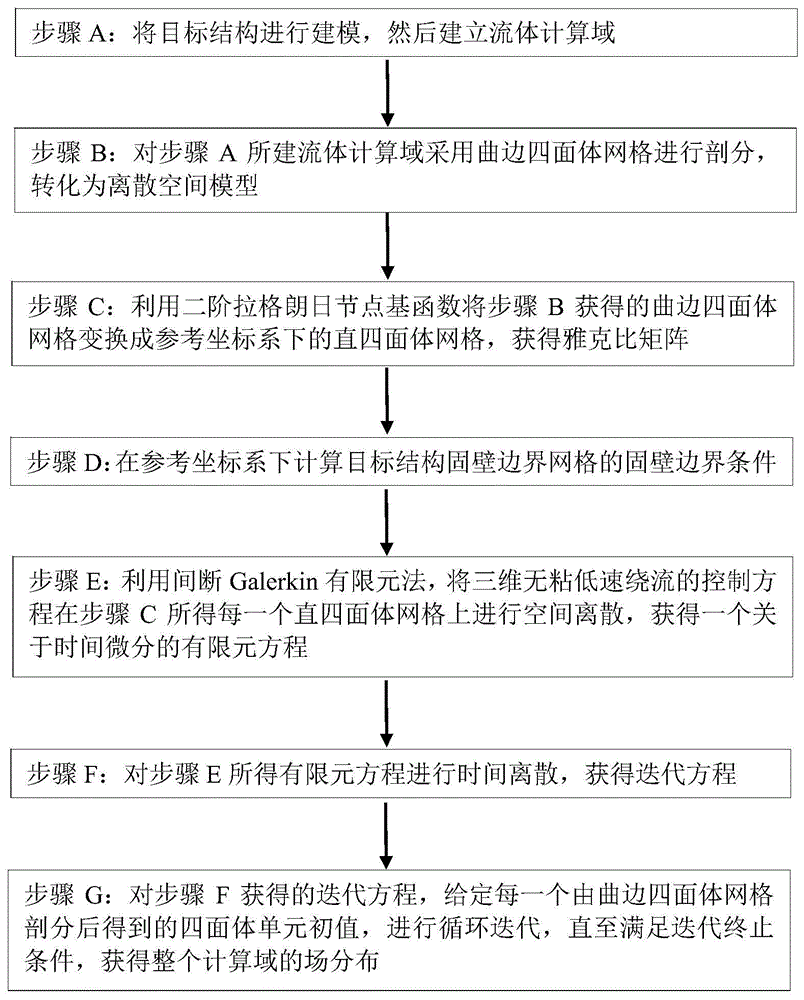
一种基于非结构曲边网格的三维无粘低速绕流的数值模拟方法，包括以下步骤：

a.将目标结构进行建模，然后建立流体计算域；

b.对步骤a所建流体计算域采用曲边四面体网格进行剖分，转化为离散空间模型；

c.利用二阶拉格朗日节点基函数将步骤b获得的曲边四面体网格变换成参考坐标系下的直四面体网格，获得雅克比矩阵；

如图4所示，曲边四面体网格是在真实的直角坐标系(x,y,z)下的表示，其中点1、2、3、4为曲边四面体网格的四个顶点，点5、6、7、8、9、10为曲边四面体网格每条边的中点，这些点的坐标信息xi,yi,zi(i＝1,2,…,10)可以通过一般网格生成程序获得，这里不再详细阐述。

如图5所示，直四面体网格是在参考坐标系(ξ,η,ζ)下的表示的标准四面体网格，顶点1的坐标为(0,0,0)，顶点2的坐标为(1,0,0)，顶点3的坐标为(0,1,0)，顶点4的坐标为(0,0,1)，点5、6、7、8、9、10为对应每条边的中点。在参考坐标系下我们定义如下二阶拉格朗日节点基函数：

其中ξ,η,ζ为参考坐标系分量。真实坐标系的分量x,y,z可以表示为：

最后直角坐标系和参考坐标系之间的变换雅克比矩阵为：

将(1)式、(2)式代入(3)式可最终求得雅克比矩阵的显示表达式，雅克比矩阵的逆表示为：

d.在参考坐标系下计算目标结构固壁边界网格的固壁边界条件；

在直角坐标系下，曲边四面体网格的边界面上的值有如下固壁边界条件：

其中u,v,w分别为直角坐标系下的速度分量；下标l,r分别表示本网格和相邻网格；表示直角坐标系的基矢量；表示曲边四面体网格中边界面上外单位法向量；ρ,p分别为密度和压力。由于在边界上，曲边四面体网格的边界面没有相邻网格，因此我们通过(5)式来构造相邻网格在边界面上的值，即为固壁边界条件。曲边四面体网格中，由于其边界面为曲面因此无法直接计算(5)式，需要在参考坐标系下的直四面体网格中计算。

基于参考坐标系，有：

其中，为参考坐标系下直四面体网格中边界面上外单位法向量。则有：

其中：

将(6)式，(8)式代入(5)式。最后，参考坐标系下直四面体网格中的边界面上的值有如下固壁边界条件：

e.利用间断galerkin有限元法，将三维无粘低速绕流的控制方程在步骤c所得每一个直四面体网格上进行空间离散，获得一个关于时间微分的有限元方程；

对于无粘绕流问题，在参考坐标系下求解如下三维守恒形式的欧拉方程：

式中q为守恒变量，d＝[fc,gc,hc]为无粘通量张量，其具体形式如下：

其中u,v,w分别为直角坐标系下的速度分量；ρ,p分别为密度和压力；e为总能；u,v,w为逆变速度。(11)式是5个方程的组合，为了表示方便我们用下标h(h＝1,2,3,4,5)表示(11)式中第h几个方程以及q和d中的第h个分量qh，dh。

在参考坐标系下，对于间断galerkin有限元法，变量在直四面体网格ω内的分布采用下面的多项式近似表达：

φj(ξ,η,ζ)表示插值基函数，在这里我们选择正交基函数，n表示插值基函数的个数。(11)式两端乘以测试函数φi(ξ,η,ζ)(i＝0,…n)，然后在ω内积分并且把(14)式代入，可以得到(11)式中第h个方程的galerkin方法弱形式：

其中为直四面体网格ω的边界，令：

上述积分项采用数值积分计算，(15)式最后简化为：

其中mh为质量矩阵，其元素为mij。对(11)式中每一个方程执行上述(14)-(18)式同样的操作。最后得到一个关于时间微分的有限元方程：

其中q＝[q1q2q3q4q5]^t，rhs＝[rhs1rhs2rhs3rhs4rhs5]^t

f.对步骤e所得有限元方程进行时间离散，获得迭代方程；

g.对步骤f获得的迭代方程，给定每一个由曲边四面体网格剖分后得到的四面体单元初值，进行循环迭代，直至满足迭代终止条件，获得整个计算域的场分布。

本发明通过非结构曲边网格来精确拟合曲面物面，然后把非结构曲边网格投影到参考坐标系获得直网格，在此基础上，计算目标结构固壁边界条件；同时开发相应的曲边网格数值模拟方法代替传统的直网格数值模拟方法，提高数值模拟方法的精度。

附图说明

图1是本发明流程图；

图2是实施例的流体计算域模型剖面图；

图3是实施例球表面网格示意图；

图4是实施例直角坐标系下曲边四面体网格示意图；

图5是实施例参考坐标系下直四面体网格示意图；

图6是实施例场分布剖视图；

图7是现有非结构直网格三维无粘低速绕流数值模拟方法场分布剖视图。

具体实施方式

下面结合附图和实施例来详细说明本发明的技术方案。

参照附图1，一种基于非结构曲边网格的三维无粘低速绕流的数值模拟方法，包括以下步骤：

a.建立球型结构的几何模型，然后建立流体计算域，其结构剖视图如图2所示。

b.对步骤a所建流体计算域采用曲边四面体网格进行剖分，转化为离散空间模型；

采用曲边四面体网格剖分步骤a所建流体计算域，剖分后的计算域被人为分割为多个三维曲边四面体网格，从而将连续的几何空间转化为离散的网格空间，球的表面网格如图3所示。

c.利用二阶拉格朗日节点基函数将步骤b获得的曲边四面体网格变换成参考坐标系下的直四面体网格，获得雅克比矩阵；

如图4所示，曲边四面体网格是在真实的直角坐标系(x,y,z)下的表示，其中点1、2、3、4为曲边四面体网格的四个顶点，点5、6、7、8、9、10为曲边四面体网格每条边的中点，这些点的坐标信息xi,yi,zi(i＝1,2,…,10)可以通过一般网格生成程序获得，这里不再详细阐述。如图5所示，直四面体网格是在参考坐标系(ξ,η,ζ)下的表示的标准四面体网格，顶点1的坐标为(0,0,0)，顶点2的坐标为(1,0,0)，顶点3的坐标为(0,1,0)，顶点4的坐标为(0,0,1)，点5、6、7、8、9、10为对应每条边的中点。在参考坐标系下我们定义如下二阶拉格朗日节点基函数：

其中ξ,η,ζ为参考坐标系分量。真实坐标系的分量x,y,z可以表示为：

最后直角坐标系和参考坐标系之间的变换雅克比矩阵为：

将(1)式、(2)式代入(3)式可最终求得雅克比矩阵的显示表达式，雅克比矩阵的逆表示为：

d.在参考坐标系下计算球形结构固壁边界网格的固壁边界条件；

在直角坐标系下，曲边四面体网格的边界面上的值有如下固壁边界条件：

其中u,v,w分别为直角坐标系下的速度分量；下标l,r分别表示本网格和相邻网格；表示直角坐标系的基矢量；表示曲边四面体网格中边界面上外单位法向量；ρ,p分别为密度和压力。由于在边界上，曲边四面体网格的边界面没有相邻网格，因此我们通过(5)式来构造相邻网格在边界面上的值，即为固壁边界条件。曲边四面体网格中，由于其边界面为曲面因此无法直接计算(5)式，需要在参考坐标系下的直四面体网格中计算。

基于参考坐标系，有：

其中，为参考坐标系下直四面体网格中边界面上外单位法向量。则有：

其中：

将(6)式，(8)式代入(5)式。最后，参考坐标系下直四面体网格中的边界面上的值有如下固壁边界条件：

e.利用间断galerkin有限元法，将三维无粘低速绕流的控制方程在步骤c所得每一个直四面体网格上进行空间离散，获得一个关于时间微分的有限元方程；

对于无粘绕流问题，在参考坐标系下求解如下三维守恒形式的欧拉方程：

式中q为守恒变量，d＝[fc,gc,hc]为无粘通量张量，其具体形式如下：

其中u,v,w分别为直角坐标系下的速度分量；ρ,p分别为密度和压力；e为总能；u,v,w为逆变速度。(11)式是5个方程的组合，为了表示方便我们用下标h(h＝1,2,3,4,5)表示(11)式中第h几个方程以及q和d中的第h个分量qh，dh。

在参考坐标系下，对于间断galerkin有限元法，变量在直四面体网格ω内的分布采用下面的多项式近似表达：

φj(ξ,η,ζ)表示插值基函数，在这里我们选择正交基函数，n表示插值基函数的个数。(11)式两端乘以测试函数φi(ξ,η,ζ)(i＝0,…n)，然后在ω内积分并且把(14)式代入，可以得到(11)式中第h个方程的galerkin方法弱形式：

其中为直四面体网格ω的边界，令：

上述积分项采用数值积分计算，(15)式最后简化为：

其中mh为质量矩阵，其元素为mij。对(11)式中每一个方程执行上述(14)-(18)式同样的操作。最后得到一个关于时间微分的有限元方程：

其中q＝[q1q2q3q4q5]^t，rhs＝[rhs1rhs2rhs3rhs4rhs5]^t

f.对步骤e所得有限元方程进行时间离散，获得迭代方程；

时间离散上采用二阶龙格库塔方法，显示二阶龙格库塔方法如下：

其中k表示时间步。上述方程是一个随时间步迭代的方程，可以通过前一个时刻k的值计算下一个时刻k+1的值。

g.对步骤f获得的迭代方程，给定每一个由曲边四面体网格剖分后得到的四面体单元初值，进行循环迭代，直至满足迭代终止条件，获得整个计算域的场分布。

根据实际问题给定所有四面体单元的初值，按照(21)式计算所有四面体单元当前时刻的值，然后再把当前时刻的值当成初值，继续计算下一时刻的值，以此反复循环迭代，直至计算结果收敛。最后根据(14)式计算每个单元的场分布，给出整个计算域的场分布。

图2示出了实施例的流体计算域模型剖视图；图6示出了实施例场分布剖视图；图7示出了现有非结构直网格三维无粘低速绕流数值模拟方法场分布剖视图。对比图6、图7的场分布可以看出实施例的场分布更加具有对称性，这更加接近真实情况，从而说明本发明相比现有技术提高了数值模拟方法的精度。