基于变分模态分解和维格纳威尔分布的行波时频分析方法与流程

本发明涉及电力系统领域，特别涉及一种基于变分模态分解(variationalmodedecomposition，vmd)和维格纳威尔分布(wigner-villedistribution，wvd)的行波时频分析方法。

背景技术：

随着电力系统规模的不断扩大，输电线路的负荷量逐年增加，电力客户对电网安全维护和运行的要求越来越高。如何快速切除故障线路并准确查找故障点位置，成为电力系统安全稳定运行的重要保障。

故障行波具有响应速度快，不受分布式电容、系统振荡、互感器饱和等因素的影响，具有较为明显的技术优势，故障行波保护和定位技术在理论上具有较高的定位精度和可靠性，在输电线路中获得了广泛的应用。目前，故障行波保护和定位方法主要分为以下两种：基于时域信息和基于频域信息；基于时域信息的行波保护和定位方法，需要准确检测初始行波波头的幅值、极性和到达时刻，并正确辨识后续折、反射波形的性质，对采样率要求较高，特别在高阻接地故障或电压过零点故障时，波头信息检测困难；基于频域信息的行波保护和定位方法，依据线路边界阻抗特性，根据区内、外行波信号局部高频与低频频段的比值，构成保护判据；该方法仅利用行波信号中的某两个频段信号，所包含的故障信息不充分，且当故障位置距离检测点较远时，高频信号衰减严重，可能导致保护难以正确区分线路末端故障与对端母线故障。现有的行波保护和定位方法仅基于时域信息或频域某两个频段信息，导致行波保护和定位可靠性较低，在高阻接地故障、电压过零点故障和基于单端测量的行波定位方法，实际应用定位误差较大，甚至失败。

故障行波是宽频带信号，即包含高频分量，也包含低频分量，特别是工频分量，融合故障行波时-频域全景信息，实现基于行波时-频域全景信息的保护和定位方法，有望解决现有方法存在可靠性和准确度不高的难题。但是到目前为止，还没有完整的行波时-频分析方法。

技术实现要素：

为了解决上述技术问题，本发明提供一种行波全波形真实、可靠的时频分析方法：基于变分模态分解和维格纳威尔分布的行波时频分析方法。

本发明解决上述问题的技术方案是：一种基于变分模态分解和维格纳威尔分布的行波时频分析方法，包括以下步骤：

s1：在线路上安装行波传感器，检测故障行波信号；将三相电压行波信号进行变换，获得电压行波线模分量uα(t)；

s2：对电压行波线模分量uα(t)进行变分模态分解，产生k个固有模态分量{uk(t)}＝{u1，u2，u3，......，uk}；

s3：对得到的每个固有模态分量{uk(t)}进行维格纳威尔分析；

s4：将各个固有模态分量{uk(t)}的维格纳威尔分析结果进行线性叠加，最终得到原始信号行波线模分量uα(t)的时-频域分布。

上述基于变分模态分解和维格纳威尔分布的行波时频分析方法，所述步骤s1中，采用凯伦贝尔相模变换对三相电压行波信号进行变换，凯伦贝尔相模变换的过程为：式中uα、uβ为线模电压，u0为零模电压，ua、ub、uc为相电压。

上述基于变分模态分解和维格纳威尔分布的行波时频分析方法，所述步骤s2中，对电压行波线模分量uα(t)进行变分模态分解的算法流程按以下步骤进行：

s201：假定原信号uα(t)被分为k个有限带宽的模态分量{uk(t)}，对uα(t)进行傅里叶变换，将频谱搬移至频谱中心，得到频谱信号

s202：初始化k个模态分量对应中心频率{ω1k}，拉格朗日乘子迭代次数n，均设初始值为0，其中，表示为第k个模态分量的初始迭代值，ω¹k表示第k个模态分量的中心频率初始迭代值，是拉格朗日乘子初始迭代值；

s203：随着迭代次数n每增加一次，使用交替方向乘子法更新各个模态分量其更新方法：

n←n+1

其中，c是二次惩罚因子，表示带宽参数；是拉格朗日乘子；1≤i≤k，i≠k，当i＜k，当i＞k，表示第k个模态分量经过n次迭代后得到的更新值，并用于第n+1次迭代过程的更新计算，表示第k个模态分量经过(n-1)次迭代后得到的更新值，并用于第n次迭代过程的更新计算；

更新各个模态分量对应中心频率{ωⁿ⁺¹k}，其更新方法：

表示第k个模态分量对应的中心频率经过n次迭代后得到的更新值，并用于第n+1次迭代过程的更新计算；

更新拉格朗日乘子其更新方法：

式中，γ表示噪声容限函数，表示经过n次迭代后得到的拉格朗日乘子更新值，并可用于第n+1次迭代过程的更新计算；

s204：当迭代结果，满足：

则停止迭代，否则返回步骤s203继续迭代，其中ε是判别条件给定精度；式中，1≤k≤k；

s205：将获得的k个频域模态分量进行傅里叶逆变换，取实部即可得到时域模态分量{uk(t)}。

上述基于变分模态分解和维格纳威尔分布的行波时频分析方法，所述步骤s2中，对电压行波线模分量uα(t)进行变分模态分解的过程，分为对变分问题的构造和求解的过程，具体包括以下步骤：

(1)构造变分问题：假定原信号uα(t)被分为k个有限带宽的模态分量{uk(t)}，并使得每个模态函数的有限带宽之和最小，k个模态函数即为所求；具体包括以下构造步骤：

1)通过hilbert变换，得到k个模态函数的频谱：

式中，*是q卷积，δ(t)是单位脉冲函数，t为时间；uk(t)为第k个时域模态函数(1≤k≤k)；

2)利用指数进行修正，将模态函数频谱修正至各自估算的中心频率，得：

3)通过高斯平滑估计，即l²范数梯度的平方根，对各模态函数的有限带宽进行估计，最后通过求得各模态函数有限带宽之和最小，完成对信号uα(t)的变分约束问题的构造，变分模型如下：

其中，{uk}＝{u1，u2，u3，......，uk}为分解得到的k个时域模态分量；

{ωk}＝{ω1，ω2，ω3，......，ωk}为各模态分量的中心频率；

∑kuk(t)表示：

(2)求解变分问题：为了求解上述优化问题，变分模态分解分别利用了二次惩罚相和拉格朗日乘子法，并引入增广拉格朗日函数ξ，如下式所示：

式中，c是二次惩罚因子，表示带宽参数，λ(t)表示拉格朗日乘子，∑kuk表示：然后再用交替方向乘子法进行交替迭代更新和{λⁿ⁺¹}，求得ξ的‘鞍点’；

其中，的取值问题表示为：

式中：交替方向乘子法要求时域模态函数分量uk都是可积的，且平方可积到二阶导数，所有满足上述性质的时域模态函数分量uk，都属于x的取值范围；c表示二次惩罚因子，ωk等同于∑iui(t)等同于∑i≠kuiⁿ⁺¹(t)，其中，1≤i≤k，i≠k，当i＜k，当i＞k，表示第k个时域模态分量经过n次迭代后得到的更新值，并用于第n+1次迭代过程的更新计算，表示第k个时域模态分量经过(n-1)次迭代后得到的更新值，并用于第n次迭代过程的更新计算；；表示使目标函数取得最小值时的变量值x，即λⁿ(t)表示经过(n-1)次迭代后得到的时域拉格朗日乘子更新值，并用于第n次迭代过程的更新计算。

利用parseval/plancherel傅里叶等距变换，将上式转变到频域：

式中，交替方向乘子法要求模态函数和uk(t)都是可积的，且平方可积到二阶导数，所有满足上述性质的和uk(t)，都属于x的取值范围；ω为角速度；表示频域线模分量；另外，1≤i≤k，i≠k，当i＜k，当i＞k，表示经过(n-1)次迭代后得到的频域拉格朗日乘子更新值，并用于第n次迭代过程的更新计算。

将上式第一项的ω用ω-ωk代替，

再将上式转换为非负频率区间积分的形式：

此时，得到泛函数的更新方法：

式中，对进行傅里叶逆变换，取实部即得到时域模态分量{uk(t)}；

根据上述的更新过程，同样求得泛函数的更新方法：

式中，为当前第k个模态函数频率谱的中心。

上述基于变分模态分解和维格纳威尔分布的行波时频分析方法，所述步骤s3中，对步骤2中得到的k个时域模态分量{uk(t)}分别进行维格纳威尔分析，得到各时域模态分量{uk(t)}对应的时频分布各个模态分量uk(t)的维格纳威尔分布表示为：

式中，uk^*(t)为信号uk(t)的复数共轭，为信号的瞬时相关函数，τ为时间因子，ω为角速度。

上述基于变分模态分解和维格纳威尔分布的行波时频分析方法，所述步骤s4中，将各个固有模态分量{uk(t)}经维格纳威尔分析所得时频分布线性叠加，最终得到原始信号uα(t)的时-频域分析图，含有时间、频率、幅值及极性在内的全景行波信息，定义为行波全波形。

本发明的有益效果在于：本发明首先检测故障行波信号，将三相电压行波信号，进行凯伦贝尔相模变换，获得行波线模分量；然后对行波线模分量进行变分模态分解，产生多个固有模态分量；再对得到的每个固有模态分量进行wigner-ville分析；最后将各个固有模态分量的分析结果进行线性叠加，最终得到原始行波线模信号uα(t)的时-频域分析图。本发明不仅可以抑制wigner-ville分布交叉项的干扰，还可以保留vmd良好的噪声抑制作用，保留wigner-ville分布较高的时频分辨率和良好的时频聚集性，真实、准确的展现时-频域信息特征，为基于行波信号的保护和故障定位方法的实际应用开辟了一种新思路，对故障行波保护和定位的实用化具有很重要的理论与现实意义。

附图说明

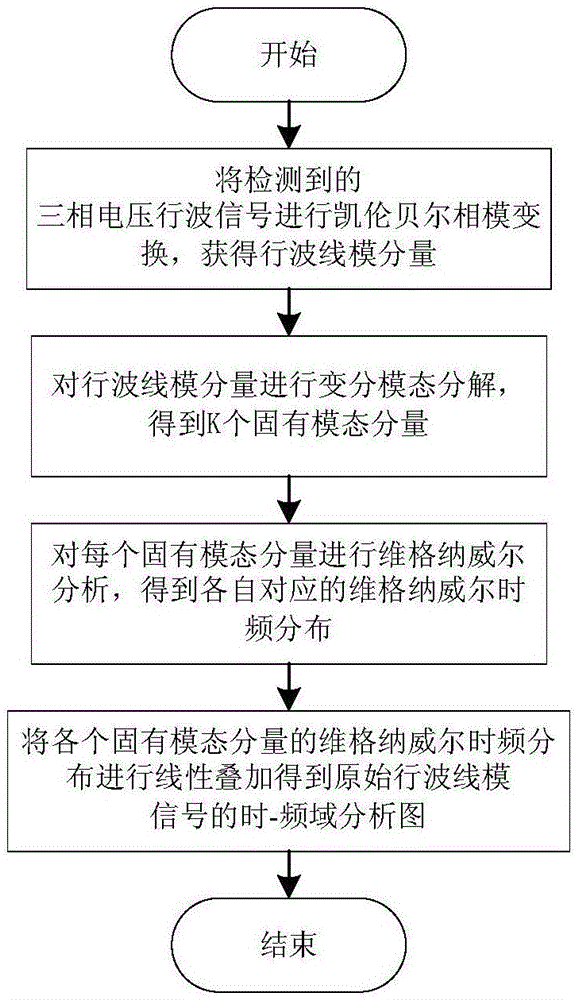
图1为本发明的流程图。

图2为染噪后的模拟仿真行波信号示意图。

图3为染噪后模拟仿真行波信号的winger-ville分布示意图。

图4为染噪后的仿真模拟行波信号的vmd-wv分布示意图。

图5为某典型高压输电线路示意图。

图6为m点检测的实际故障行波波形示意图。

图7为m点检测的实际故障行波的vmd-wvd时-频分布图。

具体实施方式

下面结合附图和实施例对本发明作进一步的说明。

如图1所示，一种基于变分模态分解和维格纳威尔分布的行波时频分析方法，包括以下步骤：

s1：在线路上安装行波传感器，检测故障行波信号；将三相电压行波信号，进行凯伦贝尔相模变换，获得行波线模分量uα(t)；凯伦贝尔相模变换的过程为：式中uα、uβ为线模电压，u0为零模电压，ua、ub、uc为相电压。

s2：对电压行波线模分量uα(t)进行变分模态分解，产生k个固有模态分量{uk(t)}＝{u1，u2，u3，......，uk}。对电压行波线模分量uα(t)进行变分模态分解的过程，分为对变分问题的构造和求解的过程，具体包括以下步骤：

(1)构造变分问题：假定原信号uα(t)被分为k个有限带宽的模态分量{uk(t)}，并使得每个模态函数的有限带宽之和最小，k个模态函数即为所求；具体包括以下构造步骤：

1)通过hilbert变换，得到k个模态函数的频谱：

式中，*是q卷积，δ(t)是单位脉冲函数，t为时间；uk(t)为第k个模态函数(1≤k≤k)；

2)利用指数进行修正，将模态函数频谱修正至各自估算的中心频率，得：

3)通过高斯平滑估计，即l²范数梯度的平方根，对各模态函数的有限带宽进行估计，最后通过求得个模态函数有限带宽之和最小，完成对信号uα(t)的变分约束问题的构造，变分模型如下：

其中，{uk}＝{u1，u2，u3，......，uk}为分解得到的k个模态分量；

{ωk}＝{ω1，ω2，ω3，......，ωk}为各模态分量的中心频率；

∑kuk表示：

(2)求解变分问题：为了求解上述优化问题，变分模态分解分别利用了二次惩罚相和拉格朗日乘子法，并引入增广拉格朗日函数ξ，如下式所示：

式中，c是二次惩罚因子，表示带宽参数，λ(t)表示时域拉格朗日乘子。

然后再用交替方向乘子法进行交替迭代更新{uⁿ⁺¹k}、{ωⁿ⁺¹k}和{λⁿ⁺¹}，求得ξ的‘鞍点’；

其中，的取值问题表示为：

式中：交替方向乘子法要求时域模态函数分量uk都是可积的，且平方可积到二阶导数，所有满足上述性质的时域模态函数分量uk，都属于x的取值范围；uk∈x，c，表示二次惩罚因子，ωk等同于∑iui(t)等同于∑i≠kuiⁿ⁺¹(t)，其中，1≤i≤k，i≠k，当i＜k，当i＞k，表示第k个时域模态分量经过n次迭代后得到的更新值，并用于第n+1次迭代过程的更新计算，表示第k个时域模态分量经过(n-1)次迭代后得到的更新值，并用于第n次迭代过程的更新计算；；表示使目标函数取得最小值时的变量值x，即λⁿ(t)表示经过(n-1)次迭代后得到的时域拉格朗日乘子更新值，并可用于第n次迭代过程的更新计算。

利用parseval/plancherel傅里叶等距变换，将上式转变到频域：

式中，交替方向乘子法要求模态函数和uk(t)都是可积的，且平方可积到二阶导数，所有满足上述性质的和uk(t)，都属于x的取值范围；ω为角速度；表示第k个模态分量经过n次迭代后得到的更新值，并用于第n+1次迭代过程的更新计算，表示频域线模分量；另外，1≤i≤k，i≠k，当i＜k，当i＞k，表示经过(n-1)次迭代后得到的拉格朗日乘子更新值，并可用于第n次迭代过程的更新计算。

将上式第一项的ω用ω-ωk代替，

再将上式转换为非负频率区间积分的形式：

此时，得到泛函数的更新方法：

式中，对进行傅里叶逆变换，取实部即得到时域模态分量{uk(t)}

根据上述的更新过程，同样求得泛函数的更新方法：

式中，为当前第k个模态函数频率谱的中心。

因此，综合上述构造和求解的过程，步骤s2具体包括以下步骤：

s201：假定原信号uα(t)被分为k个有限带宽的模态分量{uk(t)}，对uα(t)进行傅里叶变换，将频谱搬移至频谱中心，得到频谱信号

s202：初始化k个模态分量对应中心频率{ω¹k}，拉格朗日乘子迭代次数n，均设初始值为0，其中，表示为第k个模态分量的初始迭代值，ω¹k表示第k个模态分量的中心频率初始迭代值，是拉格朗日乘子初始迭代值；

s203：随着迭代次数n每增加一次，使用交替方向乘子法更新各个模态分量其更新方法：

n←n+1

其中，c是二次惩罚因子，表示带宽参数；是拉格朗日乘子，其中，1≤i≤k，i≠k，当i＜k，当i＞k，表示第k个模态分量经过n次迭代后得到的更新值，并用于第n+1次迭代过程的更新计算，表示第k个模态分量经过(n-1)次迭代后得到的更新值，并用于第n次迭代过程的更新计算；

更新各个模态分量对应中心频率{ωⁿ⁺¹k}，其更新方法：

表示第k个模态分量对应的中心频率经过n次迭代后得到的更新值，并用于第n+1次迭代过程的更新计算；

更新拉格朗日乘子其更新方法：

式中，γ表示噪声容限函数，表示经过n次迭代后得到的拉格朗日乘子更新值，并可用于第n+1次迭代过程的更新计算；

s204：当迭代结果，满足：

则停止迭代，否则返回步骤s203继续迭代，其中ε是判别条件给定精度；式中，1≤k≤k；

s205：将获得的k个频域模态分量进行傅里叶逆变换，取实部即可得到时域模态分量{uk(t)}。

s3：对步骤2中得到的k个时域模态分量{uk(t)}分别进行wigner-ville分析，得到各时域模态分量{uk(t)}对应的时频分布各个模态分量uk(t)的wigner-ville分布表示为：

式中，uk^*(t)为信号uk(t)的复数共轭，为信号的瞬时相关函数，τ为时间因子，ω是角速度，ω＝2πf，f是频率。

s4：将各个固有模态分量{uk(t)}经wigner-ville分析所得时频分布线性叠加，最终得到原始信号uα(t)的时-频域分析图，含有时间、频率、幅值及极性在内的全景行波信息，定义为行波全波形。

实施例一：仿真模拟行波信号的时频分析

为了验证本方法对故障行波信号时-频分析的有效性，依据故障行波的数学模型构造了一个故障行波仿真模拟信号，为更好地体现行波波头时频联合分析，该模拟信号由波头r1、r2和高斯分布噪声vk组成，如公式(1)所示：

式中，t表示时间，zk为仿真模拟行波信号，r1、r2为单指数和双指数衰减振荡函数，用来模拟高频初始行波和后续行波反射波，考虑到初始行波传输和传变过程中的色散现象，f1和f2取不同频率：10khz和3khz；a1和a2是行波波头r1、r2的幅值；vk是噪声，它遵从高斯分布，其中μ为高斯分布的均值，σ²为高斯分布的方差，μ＝0，σ²＝1；t0为行波波头到达检测点的起始时刻；τ为衰减时间常数。

仿真模拟信号中各分量的参数如表1所示，采样频率为fs＝0.1mhz。

表1仿真模拟信号中各分量参数

染噪后的仿真模拟行波信号如图2所示。采用winger-ville分析进行时频分析，分析结果如图3所示。可以看出：仿真模拟行波信号zk的winger-ville分布有两个自项，其时频分布和模拟信号r1、r2的时间位置、频率中心(ti，fi)相同，分别为：(2×10^-3ms，1×10⁴hz)，(5×10^-3ms，3×10³hz)；zk的winger-ville分布含有一个交叉项，其时频位置在两个自项的中心连线上，位置大致在每一个交叉项都位于产生它的自项的几何中心，其振荡频率取决于两个自项的时间和频率距离，两个自项距离越远，其衰减速度越快，winger-ville分布的交叉项能量越小，如图3所示，由于自项距离较远，从等高线的颜色可以看出交叉项能量要小于自项；由于原始信号中噪声的干扰，两个自项受噪声干扰严重。

为抑制winger-ville分解中存在的交叉项，将染噪后的仿真模拟行波信号zk先进行变分模态分解，自适应的分解得到两个单分量信号的模态函数，然后对两个模态分量进行winger-ville分析，并线性叠加，最终得到染噪后的仿真模拟行波信号的基于vmd和wigner-ville分布的时-频分布图，如图4所示，从图中可以看出基于vmd和wigner-ville分布的时频分析方法有效消除了wigner-ville分布中的交叉项，具有较高的时频分辨率和良好的时频聚集性，对噪声具有良好的抑制作用。

实施例二：实际故障行波信号的时频分析

图5所示一500kv高压输电线路，在与检测点m相距25km的位置f1发生单相接地故障(过渡电阻为rk为50ω/故障初相角δ°为90°)，故障分量uaf与该点正常负荷状态下的电压大小相等方向相反，采样率取0.1mhz。在检测点m检测到的实际故障行波波形如图6所示。对图6所示时域故障行波进行vmd和wigner-ville分布分析，得到图7所示实际故障行波的基于vmd和wigner-ville分布的时-频分布图，从时-频分析图可以清晰地得到故障行波的时-频联合分布，时域图中各故障行波波头的到达时刻，与时-频分布图中的行波波头到达时刻完全吻合。