一种核反应堆堆芯子通道计算的加速方法与流程

本发明涉及核反应堆堆芯设计和安全领域，是一种核反应堆堆芯子通道计算的加速方法。

背景技术：

传统的压水堆全堆芯热工水力分析一般采单通道模型，该模型认为堆芯各个通道之间是孤立的、封闭的，不考虑与相邻通道之间的质量、动量和能量的交换，这种模型简单，计算量小，但仅适用于计算闭式通道。因此发展了子通道模型，该模型认为相邻通道冷却剂之间存在质量、动量和能量的交换。由于考虑了这种交混效应，热通道内冷却剂的焓和温度比不考虑交混时低，与之相应的燃料温度也会有所下降，这有利于提高反应堆的安全性和经济性。

但是，在子通道模型的计算中不能像单通道模型那样只计算少数热通道，而是对大量的通量进行分析，因此当进行全堆芯的子通道计算时，计算量和所消耗的计算机内存都是难以忍受的。因此，需要一种加速子通道计算和降低内存计算机消耗的方法。

技术实现要素：

为了克服上述现有技术存在的问题，本发明的目的在于提供一种核反应堆堆芯子通道计算的加速方法，是一种加速堆芯子通道计算同时降低内存消耗的方法，该方法通过采用Krylov子空间法求解全堆芯子通道计算中的大型非对称线性方程组，包括能量方程、轴向动量 方程、压力修正方程，具有较高的计算效率。

为了达到上述目的，本发明采用如下技术方案：

一种核反应堆堆芯子通道计算的加速方法，包括以下两大步骤：

步骤1：将子通道质量、能量和动量守恒非线性方程组进行线性化，定义以下三个转换函数f_ij、β_kj和β_ij’以考虑施主元的影响：

式中，

m_ij——混合物轴向质量流量；

w_kj为穿过间隔k的横流速度，为正值，与e_ik一起表示方向，e_ikw_kj大于0表示从l通道流到l′通道，否则相反；

——为间隔k的有效速度，即相邻通道有效速度的代数平均；

将式(1)中的三个转换函数代入到子通道能量、轴向动量、横向动量和质量方程中，便得到如下四个线性化后的子通道方程：

1)能量方程

式中，

f_ij、f_ij-1——通道(i,j)和(i,j-1)的转换函数；

m_ij、m_ij-1——通道(i,j)和(i,j-1)的混合物轴向质量流量；

ΔX_j——轴向节块j的高度；

w'_kj——为穿过间隔k的湍流速度；

β_kj——间隔k的转换函数

w_kj为穿过间隔k的横流速度，为正值，与e_ik一起表示方向，e_ikw_kj大于0表示从l通道流到l′通道，否则相反；

h_ij、h_nj、h_ij+1和h_ij-1——通道(i,j)、(n,j)、(i,j+1)和(i,j-1)的混合物焓值；

P_r——燃料棒r的热周，燃料棒r与通道i相邻；

Φ_ir——燃料棒r的热周与通道i相邻的份额；

q″_rj——燃料棒到流体的热流密度；

C_k——横向导热系数，如下式计算：

——以k为边界相邻的两个通道i和n的导热系数的代数平均值；

G_T——导热系数的几何因子，用于考虑子通道间由于导热引起的能量传递；

l_k——相邻两个子通道的中心距

T_ij、T_nj——通道(i,j)和(n,j)温度；

2)轴向动量方程

式中：

U'_ij、U'_ij-1——通道(i,j)和(i,j-1)的有效速度，表示控制体内的平均速度；

f_T——湍流动量因子；

v^'*——有效比体积；

A_ij、A_nj——通道(i,j)和(n,j)的横截面积

K'_ij——压降因子；

g_c——单位转换因子；

g——重力加速度；

P_ij、P_ij-1——层(i,j)和(i,j-1)处的压力；

ρ_ij——通道(i,j)的密度

θ——通道与竖直面的夹角；

3)横向动量方程

式中：

——为层j和j-1上的间隔k的有效速度，即相邻通道有效速度的代数平均；

s_k——子通道划分线k的长度

l_k——相邻两个子通道的中心距

K_G——横流摩擦压降因子；

P_kj-1——间隔k相邻两个通道的压差；4)质量守恒方程

式中：

EC_ij——质量守恒方程残差

步骤2：利用Krylov子空间法求解线性化后的子通道方程(2)～(5)，对方程系数矩阵采用压缩行非零存储技术CSR存储，CSR技术采用三个一维数组a、ia和ja来存储规模大小为m×n的系数矩阵A的非零元素及相应位置。记A矩阵中的非零元素个数为nnz，则：

1)一维数组a，数组长度为nnz，数组元素分别为系数矩阵A中从左到右，从上到下排列的非零元素值；

2)一维数组ia，数组长度为m+1，存储系数矩阵A中每一行第一个非零元素在总非零元素中的顺序，最后一个元素为nnz+1；

3)一维数组ja，数组长度为nnz，存储系数矩阵A中每一行非零元素在该行中的局部顺序。

与现有技术相比，本发明有如下突出优点：

(1)对系数矩阵采用非零存储技术，避免生成大的系数矩阵，与高斯消去法等直接法相比大大节省计算机内存。

(2)采用Krylov子空间求解子通道计算中的能量、动量和压力修正方程，与高斯赛德尔迭代、超松弛迭代等定点迭代法相比具有较高的计算效率。

附图说明

图1是轴向控制容积及变量定义示意图。

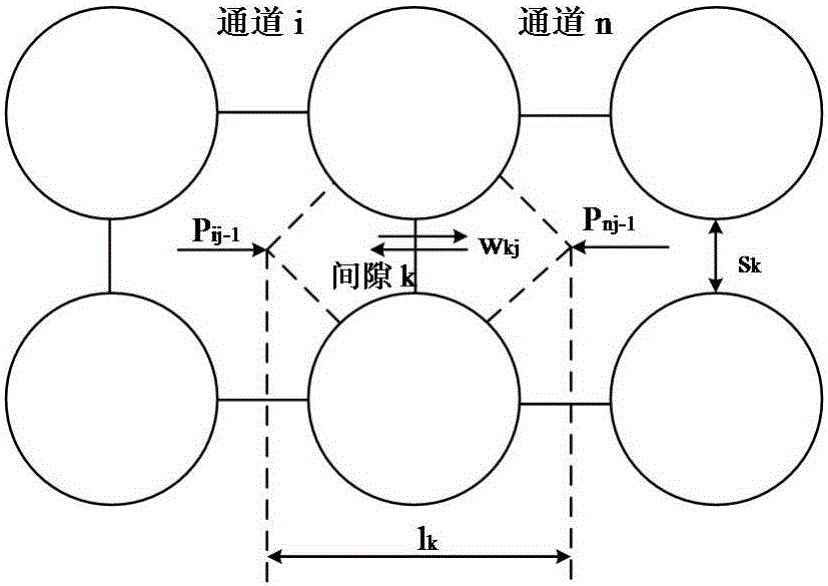
图2是横向控制容积及变量定义示意图。

图3是典型压水堆四分之一组件示意图。

图4是直接法和GMRES算法求解结果对比示意图。

具体实施方式

下面结合附图和具体实施方式对本发明做进一步详细说明：

对于图1和图2中的控制容积，稳态子通道分析求解如下差分形式的稳态守恒方程：

(1)质量守恒方程

控制体(i，j)稳态差分形式的质量守恒方程如下：

(2)能量守恒方程

稳态差分形式的能量守恒方程如下所示：

(3)轴向动量守恒方程

稳态差分形式的轴向动量守恒方程如下：

(4)横向动量守恒方程

稳态差分形式的横向动量守恒方程如下：

四个守恒方程(6)～(9)组成了非线性方程组，求解过程为将非线性方程组线性线性化，并且迭代求解。在每个线性化计算中，只求解一个变量，其它变量当作已知量求解。

通过定义式(1)中的三个转换函数得到(2)～(5)四个线性化的子通道方程。

观察式(2)可以发现，这是一个系数矩阵为五对角矩阵的线性方程组，通过求解该方程组可以得到焓h_ij的分布。

同样可以发现，式(3)是一个系数矩阵为五对角矩阵的线性方程组，通过求解该方程组可以得到焓m_ij的分布。

轴向和横向动量方程的求解中假设了压力场，一个正确的压力场 应该使计算得到的速度场满足连续性方程。但据这样给定的压力场计算而得的速度场，未必能满足连续性方程，因此要对给定的压力场作改进，即进行压力修正。

根据质量守恒方程，对于控制容积(i，j)，质量守恒残差可以写成以下形式：

为了使残差等于零，根据牛顿迭代法，对压力场进行修正：

式(11)中，

将式(12)代入式(11)整理可得到线性化后的质量方程式(5)。

通过观察可见式(5)是系数矩阵为七对角矩阵的线性方程组。

通过子通道守恒方程的推导化简可发现，能量方程、轴向动量方程、横向动量方程和压力修正方程最终求解的都是形如式(13)的线性方程组，当进行全堆芯或者四分之一堆芯的子通道计算时，该线性方程组的系数矩阵A的规模往往很大，达百万量级，因此合理科学的非零存储技术以及选取一个稳定高效的线性方程组求解方法对于节 省计算机内存和提高计算效率就显得尤为重要。

Ax＝b (13)

(1)合理科学的非零存储技术

采用压缩行非零存储技术CSR，CSR技术采用三个一维数组a、ia和ja来存储规模大小为m×n的系数矩阵A的非零元素及相应位置。记A矩阵中的非零元素个数为nnz，则：1)一维数组a，数组长度为nnz，数组元素分别为系数矩阵A中从左到右，从上到下排列的非零元素值；

2)一维数组ia，数组长度为m+1，存储系数矩阵A中每一行第一个非零元素在总非零元素中的顺序，最后一个元素为nnz+1

3)一维数组ja，数组长度为nnz，存储系数矩阵A中每一行非零元素在该行中的局部顺序；

例如对于大小为4×4的系数矩阵A：

采用CSR技术存储对应的三个一维数组分别为：

通过非零存储技术CSR，可以避免存储系数矩阵A中的零元素，对于大规模的子通道问题，例如全堆芯子通道问题，系数矩阵规模达到百万量级，CSR技术可以大大节省存储空间。

(2)稳定高效的线性方程组求解方法

线性方程组的求解方法主要包括直接法、基本迭代法和投影法。常见的直接法有高斯消去法和三角分解法，它们虽然理论简单便于实现，但是在处理大规模矩阵问题时运算量和所消耗内存太大，无法实用。相比之下，基本迭代法就更适用于高阶稀疏对角占优矩阵的求解，该方法主要包括雅克比迭代法、高斯-赛德尔迭代法和超松弛迭代法三类。但是基本迭代法在求解子通道线性化后的方程组效率不高，主要是因为子通道线性化后的方程组的系数矩阵为弱对角占优矩阵。目前求解该类线性方程组最实用高效的迭代法当属投影法了。按照投影法的思想，在求解如的线性方程组时，不是直接在n维欧几里德空间中寻找解向量，而是在的某一子空间中寻找其近似解：而这个子空间目前主要采用的是Krylov子空间，相应的线性方程组投影法也就被称为Krylov子空间解法。

对于形如的线性代数方程组，定义初始残差向量为：

式中：

——解向量的任意迭代初值。

则Rⁿ的m维Krylov子空间可记为：

Krylov子空间解法就是通过利用彼得罗夫-伽辽金条件：

从而在m维仿射子空间中寻找到方程组的近似解的。其中 L_m是另外一个m的子空间。不同的L_m选取方式，产生了不同类别的Krylov子空间解法。最典型的两种选取方式有：其一，选取 或这类方法主要是基于Arnoldi正交化过程的；其二，选取这类方法主要是基于Lanczos双正交化过程的，其中A^T为矩阵A的转置。不论如何，Krylov子空间解法实际上是做了这样一个近似：

式中：

q_m-1——m-1阶多项式。

显然，Krylov子空间解法在本质上就是采用一个多项式展开近似。

基于上述Krylov子空间理论的线性代数方程组解法种类众多，其中比较著名的如共轭梯度法(CG)、Lanczos方法以及广义极小残余方法(GMRES)等。它们各有特点，具体选取哪一种方法要视待解方程组系数矩阵的性质而定。例如CG方法和Lanzos法往往只能用在对称正定的系数矩阵的求解中；而GMRES方法除了要求系数矩阵非奇异外，几乎对矩阵性质没有其它更严格的要求。因此，GMRES方法也就成为了当今科学计算领域应用最为广泛的大型稀疏矩阵线性代数方程组Krylov子空间解法之一。下面将简要介绍GMRES基本算法。

GMRES算法是基于Arnoldi正交化过程的Krolov子空间解法。它选取了这样可以使残差向量对于子空间中的 所有向量都达到极小化，GMRES方法的典型算法如下：

(1)计算

(2)定义(m+1)×m阶矩阵并置

(3)对j＝1，2，...，m做

(4)计算

(5)对i＝1，2，...，j做：

(6)

(7)

(8)i循环结束；

(9)如果h_j+1，j＝0，则令m＝j，并跳转至12步；

(10)

(11)j循环结束；

(12)计算且(其中，V_m为以为第i列的n×m阶矩阵，为(m+1)×(m+1)阶单位阵的第一列)；

(13)结束。

可以证明，完成上述GMRES方法所需的计算量和存储量是随着子空间阶数m的增加

而分别至少呈O(m²)n和O(mn)增长的。所幸，理论上已证明上述算法所需的子空间阶数至多取到n时，迭代就可以收敛。并且在通常的实际应用中，子空间阶数m往往是远远小于n的，这也就令GMRES方 法更具有了吸引力。但是，对于某些问题，尤其是当矩阵阶数很高时，GMRES方法可能需要较高的子空间维数才能获得满足精度要求的解，这无疑会带来更大的计算负担。目前主要有两种途径来解决这个问题：周期性的重启GMRES算法以及截断Arnoldi正交化过程。其中相对执行简单、应用广泛的当属前者。以下为典型的重启GMRES算法：

(1)计算

(2)由向量开始，采用与前述GMRES算法相同的Arnoldi正交化过程，产生Arnoldi正交基V_m及矩阵

(3)计算且

(4)如果解向量满足精度要求则结束，否则置并跳转至第1步。

以上为每m步迭代实现一次重启的GMRES算法。

分别采用高斯消去法和GMRES法求解图3所示的典型压水堆四分之一组件和全组件，计算所需时间对比如图4所示，可以看到随着计算问题规模的增大，GMRES的加速效果越显著。