一种基于Bayes混合模型的命中精度评估方法与流程

本发明涉及制导系统及定位系统的精度评估领域，具体涉及一种基于Bayes混合模型的命中精度评估方法。
背景技术：
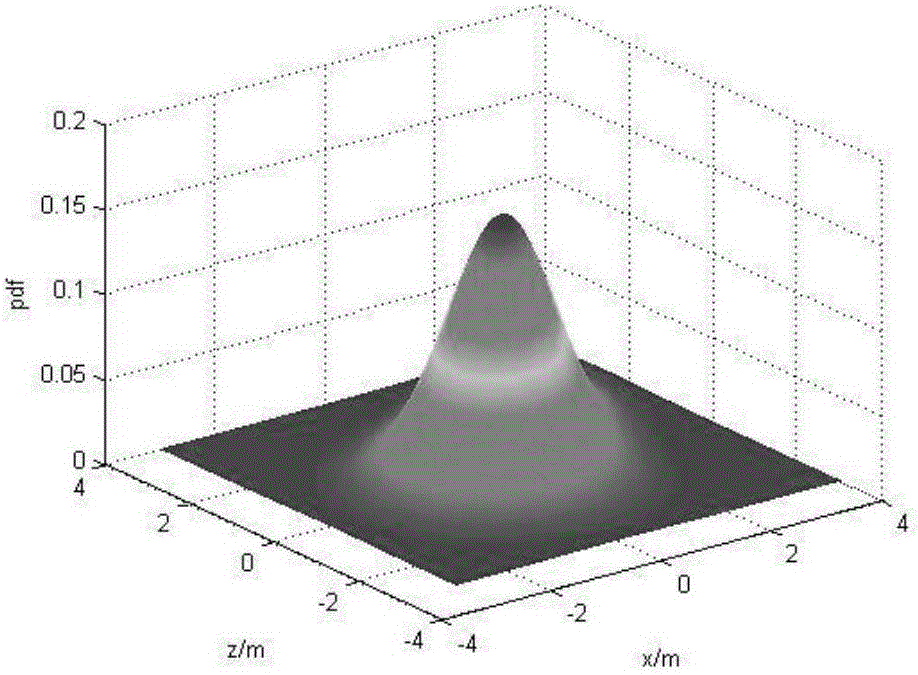
：在制导系统或定位系统的精度鉴定过程中，圆概率误差(CircularErrorProbable，CEP)是常用的精度指标之一，其优点是能够很好地融合射击准确度与密集度两项指标进行表征。CEP的概率定义为P(X2+Z2≤CEP2)＝0.5，其中(X,Z)代表纵、横向偏差。假设(X,Z)服从连续型分布f(x,z)，则CEP方程可改写成∫∫x2+z2≤CEP2f(x,z)dxdz=0.5]]>对于f(x,z)最常见的假设是正态分布，在此基础上进行CEP求解。传统CEP评估流程主要有两个难点，一是CEP方程的具体计算问题。CEP方程复杂，即使给定分布参数也难以求得精确解。在实际应用中往往根据不同的假设采用相应的简化计算公式。文献[1](WANGYan-yong,YANGGong-liu,YanDun-cai,etal.ComprehensiveAssessmentAlgorithmforCalculatingCEPofPositioningAccuracy[J],Measurement,2014,47(1):255-263)对常用的12种CEP计算方法进行了总结，并将其分为了三类：一维参数化方法，二元正态算法以及数值积分方法。由于CEP一般性方程的求解较为复杂，因此在实际应用中往往先对样本数据作分析，而后根据分析结果采用相应的简化公式。另一难点是评定结果的适应性问题，因此有必要对CEP统计量作相应的扩展。文献[2](ZHANGJian,ANWei-lian.Assessingcircularerrorprobablewhentheerrorsareellipticalnormal[J].JournalofStatisticalComputationandSimulation,2012,84(4):565-586)基于Cornish-Fish展开将传统的CEP代入型点估计推广到了纠偏型点估计，并且分别基于Bootstrap方法、渐近分布理论以及C-F展开提出了三类CEP的区间估计方法；针对分析面目标命中精度时CEP没有考虑面目标自身特性等问题，文献[3](王刚，段晓君，王正明.基于蒙特卡罗积分法的面目标精度评定方法[J].系统工程与电子技术，2009，31(7):1680-1683)将圆概率误差CEP推广到命中区域圆概率偏差(ACEP)，使精度评定结果更加合理。另外，为使落点偏差样本满足来自同一个正态总体的假设，需将不同状态的样本数据折合到同一状态，并进行异常值检验，相容性检验与正态性检验。这一过程中首先数据等效折合会因制导误差分析与分离的不准确而产生误差，从而影响整个精度评定过程；其次在异常值剔除阶段，如果物理判断不准确，会造成数据误处置，也会使CEP计算产生误差；另外由于假设检验主观性较强(检验统计量的临界值与检验的显著水平都是人为指定)，因此在这一假设下的精度评定结果的可信度不高，甚至异常。技术实现要素：本发明的目的在于克服在复合制导在不同试验条件的前提下，采用传统CEP估计方法存在的上述缺陷，基于Bayes非参数混合模型，对多条件概率分布下的CEP点估计和区间估计进行了算法设计。为了实现上述目的，一种基于Bayes混合模型的命中精度评估方法，所述方法包括：将综合试验条件划分为若干类，获取每类条件先验概率；使用聚类算法对落点偏差样本数据进行分类；在每类条件下，计算落点偏差分布的概率密度函数；由此建立多条件概率分布下的混合CEP方程，对该方程进行解算得到CEP值。上述技术方案中，所述方法具体包括：步骤1)将综合试验条件划分为h1,h2,…,hN类，N为类型总数；获取每类条件hk的先验概率p(hk)；p(hk)=e-NNkk!/Σk=1Ne-NNkk!]]>步骤2)使用聚类算法对落点偏差样本数据进行分类；步骤3)在每类hk条件下，计算落点偏差分布的概率密度函数fk(x,z|hk)；步骤4)建立多条件概率分布下的混合CEP方程；多条件概率分布为：f(x,z)=Σk=1Np(hk)fk(x,z|hk)]]>满足下式的R，即为多条件概率下的混合CEP方程为：∫∫x2+z2≤R2f(x,z)dxdz=0.5---(8)]]>步骤5)将多条件概率下的混合CEP方程转换为极坐标形式；步骤6)用数值积分方法对极坐标形式的多条件概率下的混合CEP方程进行求解得到R。上述技术方案中，所述步骤3)具体包括：步骤301)根据条件hk(k＝1,2,…,N)下的样本量为nk的精度评定样本计算样本均值、样本标准差和样本相关系数；样本均值和样本标准差为：μxk=1nkΣi=1nkxi(k)μzk=1nkΣi=1nkzi(k)σxk=1nk-1Σi=1nk(xi(k)-μxk)2σzk=1nk-1Σi=1nk(zi(k)-μzk)2---(5)]]>其中，为样本纵向落点偏差X的样本均值、样本标准差；为样本横向落点偏差Z的样本均值、样本标准差；样本相关系数ρk为：ρk=Σi=1nk[(xi(k)-μxk)(zi(k)-μzk)](nk-1)σxkσzk---(6)]]>步骤302)根据样本均值、样本标准差和样本相关系数，建立hk条件下落点偏差分布的概率密度函数；fk(x,z|hk)是(X,Z)在条件hk的概率密度函数，这里假设对于所有的条件hk(k＝1,…,N)，fk(x,zhk)都是正态分布的概率密度，即fk(x,z|hk)=12πσxkσzk1-ρk2exp{-12(1-ρk2)[(x-μxk)2σxk2-2ρk(x-μxk)(z-μzk)σxkσzk+(z-μzk)2σzk2]},---(7).]]>上述技术方案中，所述步骤4)的具体实现过程为：将多条件概率下的混合CEP方程转换为极坐标形式为：式中ak=14(1σvk2-1σuk2)bk=14(1σvk2-1σuk2)ck=1σukσvkexp{-12[(μukσuk)2+(μvkσvk)2]}---(10)]]>这里的未知参数是其值由下式给出：对样本均值和样本标准差进行去相关变换：令ξk为：ξk=12tg-12ρkσxkσzkσxk2-σzk2---(11)]]>变换后的样本均值和样本标准差为：μuk=μxkcosξk+μzksinξkμvk=μzkcosξk-μxksinξkσuk=σxk2cos2ξk+σzk2sin2ξk+2ρkσxkσzkcosξksinξkσvk=σzk2cos2ξk+σxk2sin2ξk-2ρkσxkσzkcosξksinξk---(12).]]>上述技术方案中，所述方法还包括：步骤7)采用Bootstrap方法计算混合CEP区间估计与置信上限，具体包括：步骤701)利用Bootstrap方法对样本进行重采样；给定重采样次数M(一般取M＝1000)，分别从正态总体随机抽取M组样本量为nk的独立样本(k＝1,2,…,N)，则每重采样得到的样本总数为步骤702)利用步骤6)算出M个R的代入型估计，并从小到大排序为：R(1),R(2),…,R(M)；步骤703)计算CEP的置信区间与置信上限：给定置信水平1-α，则CEP的置信区间和置信上界Rb的计算公式如下：R‾bu=RC1-α/2R‾bl=RCα/2---(16)]]>Rb=RCα---(17)]]>其中，C1-α/2、Cα/2、Cα分别为序列的第[αM]，[x]表示实数x的整数部分。本发明的优势在于：1、对于系统偏差差异较为明显的多总体落点偏差样本，利用本发明的方法得到的CEP评估结果，较之传统方法，精度更高，且更为符合CEP的“半数必中圆半径”含义；2、在小子样条件及多总体情况的前提下，即便权重选取存在部分偏差，本发明的方法的CEP计算结果比原单总体方法精度高；3、先验权重估计不准确带来的本发明的方法CEP计算结果的误差上界是可估计的，且本发明的方法提供了先验失真带来的混合CEP计算误差范围。附图说明图1为本发明的基于Bayes混合模型的命中精度评估方法的流程图图2a为混合总体的三维概率密度函数；图2b为混合总体的二维概率密度函数；图3为样本分布以及不同算法得到的CEP间的比较图；图4a为三种情况下的CEP对比值图；图4b为三种情况下的CEP偏差对比值图。具体实施方式本发明中的CEP定义方式为：以期望弹着点为圆心的落点散布圆的半径；数学表述为：以目标点为圆心建立直角坐标系，假设纵向落点偏差X和横向落点偏差Z均服从正态分布，则(X,Z)的联合概率密度函数为：f(x,z)=12πσxσz1-ρ2exp{-12(1-ρ2)[(x-μx)2σx2-2ρ(x-μx)(z-μz)σxσz+(z-μz)2σz2]}---(1)]]>式中，σx，σz是X，Z的标准差；μx，μz是X，Z的均值；ρ是X，Z的相关系数，0≤|ρ|＜1。则满足下式的R即为圆概率误差CEP：∫∫x2+z2≤R2f(x,z)dxdz=0.5---(2)]]>其中f(x,z)同式(1)；式(2)是CEP方程的一般形式。以下仅讨论ρ＝0的情况，对于ρ≠0设精度评定样本为(x1,z1),(x2,z2),…,(xn,zn)，传统的CEP评估流程是假定其来自同一个二元正态总体，用样本估计式(1)中的参数σx，σz，μx，μz，ρ，再根据式(2)利用数值积分方法估计出R。实际上由于试验环境以及目标特性等因素的影响，精度评定样本的差异较大，因此难以将其视为来自同一正态总体。结合随机密度函数的Bayes混合模型为f(y)＝∫K(y；θ)dP(θ)(3)其中K(y；θ)为参数θ取不同值的密度函数，P(θ)为随机密度函数，通常为下述离散形式P(dθ)=Σl=1∞ωlδθl(dθ)---(4)]]>先验分布记在参数θ取不同值的示性函数。对比传统的CEP定义，所谓多条件下的混合CEP是指：以期望弹着点为圆心的落点散布圆的半径，此时落点偏差服从多条件概率混合分布。复合制导在不同试验条件的前提下，会得到不同的试验精度。试验条件具有多种信息源，且各信息源情况各异，服从不同总体。由于事先并不确知一组试验中可能出现的综合条件与相应的出现概率，建模时，可以视其为随机变量，基于Bayes非参数混合模型的框架对其进行建模。不同于传统CEP评估方法中的数据等效折合思路，本发明的方法尝试从混合分布的角度进行CEP计算。假设有综合试验条件N类，(X,Z)在第k类条件下服从连续分布fk(x,z|hk)，则由Bayes非参数混合模型理论可知其中p(hk)是条件hk的先验权重。将其代入CEP方程，则可以利用经典CEP算法设计相应的混合CEP精度评定过程。如图1所示，一种基于Bayes混合模型的命中精度评估方法，所述方法包括：步骤1)将综合试验条件划分为h1,h2,…,hN类，N为类型总数；获取每类条件hk的先验概率p(hk)：p(hk)=e-NNkk!/Σk=1Ne-NNkk!]]>步骤2)设已获得待评估的横纵向落点偏差样本为且已知综合试验条件为h1,h2,…,hN类，使用系统聚类算法对样本数据进行分类，记条件hk下的落点偏差样本为其中使用系统聚类算法对落点偏差样本数据进行分类时，先将各个样品各看成一类，然后规定类与类之间的距离(这里采用欧式距离)，选择距离最小的一对合并成新的一类，计算新类与其他类之间的距离，再将距离最近的两类合并，这样每次减少一类，直至所有的样本合为一类为止；步骤3)在每类hk条件下，计算落点偏差分布的概率密度函数；具体包括：步骤301)根据条件hk(k＝1,2,…,N)下的样本量为nk的精度评定样本计算样本均值、样本标准差和样本相关系数；样本均值和样本标准差为：μxk=1nkΣi=1nkxi(k)μzk=1nkΣi=1nkzi(k)σxk=1nk-1Σi=1nk(xi(k)-μxk)2σzk=1nk-1Σi=1nk(zi(k)-μzk)2---(5)]]>其中，为样本纵向落点偏差X的样本均值、样本标准差；为样本横向落点偏差Z的样本均值、样本标准差；样本相关系数ρk为：ρk=Σi=1nk[(xi(k)-μxk)(zi(k)-μzk)](nk-1)σxkσzk---(6)]]>步骤302)根据样本均值、样本标准差和样本相关系数，建立hk条件下落点偏差分布的概率密度函数；fk(x,z|hk)是(X,Z)在条件hk的概率密度函数，这里假设对于所有的条件hk(k＝1,…,N)，fk(x,z|hk)都是正态分布的概率密度，即fk(x,z|hk)=12πσxkσzk1-ρk2exp{-12(1-ρk2)[(x-μxk)2σxk2-2ρk(x-μxk)(z-μzk)σxkσzk+(z-μzk)2σzk2]},---(7)]]>步骤4)建立多条件概率分布下的混合CEP方程：设落点偏差(X,Z)服从的多条件概率分布为：f(x,z)=Σk=1Np(hk)fk(x,z|hk)]]>满足下式的R，即为多条件概率下的混合CEP∫∫x2+z2≤R2f(x,z)dxdz=0.5---(8)]]>步骤5)将多条件概率下的混合CEP方程转换为极坐标形式：式中ak=14(1σvk2-1σuk2)bk=14(1σvk2-1σuk2)ck=1σukσvkexp{-12[(μukσuk)2+(μvkσvk)2]}---(10)]]>这里的未知参数是其值由下式给出：对样本均值和样本标准差进行去相关变换：令ξk为：ξk=12tg-12ρkσxkσzkσxk2-σzk2---(11)]]>变换后的样本均值和样本标准差为：μuk=μxkcosξk+μzksinξkμvk=μzkcosξk-μxksinξkσuk=σxk2cos2ξk+σzk2sin2ξk+2ρkσxkσzkcosξksinξkσvk=σzk2cos2ξk+σxk2sin2ξk-2ρkσxkσzkcosξksinξk---(12)]]>步骤6)用数值积分方法对极坐标形式的多条件概率下的混合CEP方程进行求解得到R；令：的形式已知，且不含未知参数。再记则式(9)可简写为G(R)＝0(15)即要求解的CEP就是函数G(R)的零点。这里采用二分法求解式(14)：(a)设置二分法精度ε，给出初次二分的上下界：Rl，Rh，满足Rl＜Rh，且G(Rl)≤0≤G(Rh)；(b)如果|G(Rl)|≤ε或|G(Rh)|≤ε，则R＝Rl或R＝Rh即为所求；否则转到(c)；(c)此时有G(Rl)＜0＜G(Rh)，令Rm＝(Rl+Rh)/2，如果|G(Rm)|≤ε，则R＝Rm即为所求；否则转到(d)；(d)如果G(Rm)＜0，则令Rl＝Rm，否则令Rh＝Rm，转到(b)。此外，所述方法还包括：步骤7)采用Bootstrap方法计算混合CEP区间估计与置信上限，具体包括：步骤701)利用Bootstrap方法对样本进行重采样；给定重采样次数M(一般取M＝1000)，分别从正态总体随机抽取M组样本量为nk的独立样本(k＝1,2,…,N)，则每重采样得到的样本总数为步骤702)利用步骤5)算出M个R的代入型估计，并从小到大排序为：R(1),R(2),…,R(M)；步骤703)计算CEP的置信区间与置信上限：给定置信水平1-α，则CEP的置信区间和置信上界Rb的计算公式如下：R‾bu=RC1-α/2R‾bl=RCα/2---(16)]]>Rb=RCα---(17)]]>其中，C1-α/2、Cα/2、Cα分别为序列的第[αM]，[x]表示实数x的整数部分。下面采用三个实例对本发明的方法进行进一步的验证。实例1：设一组试验的综合试验条件分为h1和h2，其概率的均值分别为E[p(h1)]＝0.4，E[p(h2)]＝0.6。纵、横向落点偏差(X,Z)在条件h1和h2下分别服从正态分布和则混合总体的概率密度函数如图2a和2b所示。如图2a所示，此混合总体的性态仍为单峰。将以上参数代入式(2)，可以算得混合总体下CEP的理论值为1.414m。分别从这两个分布中随机抽取样本量为20和30的样本，样本点的分布如图2b所示。以混合CEP算法得到的结果为1.420m；传统CEP算得的结果是1.215m。如图3所示，如果将50个样本视作来自于同一个正态总体，则只有8个样本(16％)落入以传统CEP为半径的圆内，这与CEP的定义不符；而有28个样本(56％)落入以混合CEP为半径的圆内，说明本文提出的方法对这一类算例的适应性较好，并且通过与理论CEP值的对比，可知对于这一组样本，混合CEP计算方法精度比传统CEP评估方法的精度高。为抑制结果的随机性，在给定先验概率，样本量，以及两总体正态参数的情况下，分别再进行10和100次抽样计算，得到的多次抽样下混合CEP和传统CEP计算结果对比(均值)结果如表1所示：表1多次抽样下混合CEP和传统CEP计算结果对比(均值)表1的结果表明，多次抽样下，混合模型CEP均值的精度高于传统算法，并且给定样本下混合CEP精度高的概率很大(100次试验精度高的比例约为77％)。另外从CEP半数必中圆的角度来看，混合CEP圆内包含样本的比例较为符合定义(100试验的均值约为44％)，而传统算法的结果离50％有较大差距(约为21％)。实例2：本例以两正态混合总体为基础讨论先验概率对混合总体CEP结果的影响，参数同实例1。此时的先验参数只有p1∈[0,1]。为分析p1与混合CEP间的响应关系，在p1的取值区间内等间隔选取21个点，分别计算CEP，结果如图4a和4b所示。其中图4a中虚线表示真实先验p1＝0.4对应的理论CEP。通过图4b可以更清楚地看到先验失真下的CEP与真实CEP，以及线性预测值的差异。首先以线性拟合函数预测先验概率与CEP的响应关系的趋势基本吻合，形式上近似二次多项式函数；其次先验失真下的CEP的最大偏差值在边界取得，这也验证了之前的结论：先验失真使CEP计算值产生偏差的偏差上界是可估计的。实例3：下面考虑小子样情形下的CEP评估问题。综合试验条件分为3类，试验后得到27个精度评定样本，每类试验条件下样本数为9。试验条件概率的真实均值和先验估计值见表2，精度评定样本见表3。针对先验有偏和先验准确的情况，分别计算混合CEP点估计以及80％和90％的CEP置信上界和置信区间，并与单总体情况下的结果进行比较，结果见表4。表2试验条件的概率的真实均值与先验估计值综合试验条件123概率的实际均值1/31/31/3先验概率估计值3/103/102/5表3落点偏差值(m)表4不同假设下的CEP计算结果(m)由于此时样本量较小，CEP点估计的结果可能不准确，所以这里主要对比不同假设下的CEP上限。如表4所示，以权重先验信息准确时的多总体CEP估计结果为比对标准，多总体权重先验存在部分偏差的混合CEP算法仍比单总体CEP算法的估计结果更为准确。这说明小子样情况下混合CEP算法的适应性和稳健性较好。当前第1页1 2 3