一种谐振式陀螺的稳定性分析方法与流程

本发明属于惯性技术领域，涉及一种谐振式陀螺，特别涉及一种直接频率输出谐振式陀螺的稳定性分析方法，适用于中低精度的低成本导航系统及定位、定向系统等。

背景技术：

谐振式陀螺是利用谐振原理作为陀螺检测机理。这种陀螺直接检测谐振器的谐振频率变化来检测角速度，而频率输出特性是一个参数激励动态特性，表征为变系数参数激励线性微分方程。

基于已有分析知，变系数参数激励线性微分方程的稳定性区间为一系列离散区间，区间的分布呈现很强的非线性特性。如果参数的选择处于不稳定区间内，则谐振系统响应就会呈现发散状态。导致谐振系统进入非线性振动状态甚至破坏结构。同时作为敏感元件的谐振系统工作过程又需要保证恰当的灵敏度，且参数的选择应该接近于不稳定区间以保证谐振子对参数变化能够灵敏的反应。因此合理设计选择谐振式陀螺参数是优化设计谐振式陀螺的首要问题。如果能够制定合理的参数选择方案，给出稳定性随参数变化的规律，改善性能指标，将会给此类陀螺的应用带来非常广阔的前景，也会对惯性导航领域的技术发展做出突出的贡献。

有时变系数参数激励线性微分方程稳定性解专指那些具有周期为π或2π的解。而实际上，一个微分方程，尽管它的系数是单值、连续的周期函数，它的解却不一定是周期函数，即使有周期函数解，其周期也不一定与方程系数的周期相同。只有当参数δ和ε满足一定的关系时，方程才有周期为π或2π的解。找出δ和ε之间的这种关系是变系数参数激励线性微分方程理论的中心问题之一。

适用于参数激励系统确定稳定性、特征指数以及划分稳定性和不稳定性边界的方法主要有三类。第一类用hill的无穷行列式方法。第二类是各种摄动方法，即基于变系数项在某种意义上小量的假定。第三类方法是应用lyapunov稳定性理论，这种方法受到的限制是要求能找到一个适当的lyapunov函数。对于正则系统可能利用hamilton函数，但对于其他系统，也许不能找到lyapunov函数。利用这种方法，人们可以定性的确定系统在大范围内的稳定性，但不能定量的确定系统的响应。

技术实现要素：

本发明要解决的技术问题为：克服现有方法的不足，提出一种谐振式陀螺稳定性分析方法，该方法得到了稳定性参数区域分布图，构建了lyapunov函数，有效地取得了振式陀螺稳定性的参数取值范围。

本发明解决上述技术问题采用的技术方案为：一种谐振式陀螺稳定性分析方法，利用谐振式陀螺参数激励特性动态模型，获得模型的稳定性参数区域分布图，构建lyapunov函数，获得模型稳定性的参数取值范围，具体步骤如下：

第一步，建立谐振式陀螺的谐振子在驱动力作用下工作在谐振状态时，最简化的动力学微分方程：其中，m表示谐振子的质量，x表示谐振子的振幅，k表示谐振子的刚度；

第二步，利用小参数法对谐振式陀螺的谐振子动力学微分方程求解，得到谐振式陀螺的稳定性参数区域分布图；

第三步，建立谐振式陀螺动力学模型的lyapunov函数，以陀螺动力学模型稳定性作为转换条件，从而得到陀螺稳定性工作的参数取值范围；

进一步的，所述步骤(1)的具体实现过程：

(1)谐振式陀螺谐振子的动力学微分方程描述为一个含有质量、阻尼和刚度的二阶微分方程：其中，m表示谐振子的质量，x表示谐振子的振幅，c表示谐振子受到的阻尼，k表示谐振子的刚度，f(t)表示谐振子的受到的科氏力；

(2)当谐振式陀螺的谐振子处于谐振状态时，使谐振子处于持续振动状态的作用力与系统的阻尼力相平衡，此时谐振子的运动规律表述为最简的动力学微分方程：

进一步的，所述步骤(2)中小参数法的具体实现过程：

(1)谐振式陀螺谐振子的动力学微分方程转化为方程：其中，q表示谐振子的振动位移，z是一个时间变量，k＝δ+εcos2z表示谐振子的振动刚度，它随着科氏力作用的变化而变化；当谐振子质量保持不变时，致使谐振子谐振频率发生变化；参数δ表示谐振子自身的固有频率，参数ε看作与谐振式陀螺参数相关的一个常量，扰动项εcos2z表示在质量块驱动的作用下对谐振子的弹性系数的调制；

(2)选取合适的小参数ε。参数δ表示谐振子自身的固有频率，一般为几千赫兹，所选的参数ε会低于参数δ小数点后一到两个数量级，故命名为小参数；

(3)谐振子的动力学微方程中含有参数δ，把参数δ固定在某些值附件，在参数平面(δ，ε)上研究方程的稳定性区域。

进一步的，所述步骤(3)参数取值范围的具体实现过程：

(1)依据谐振式陀螺谐振子的动力学微分方程构建lyapunov函数；

(2)依据lyapunov函数倒数半负定得到陀螺稳定性参数取值范围。

本发明的原理在于：参数激励振动系统的运动微分方程，系数是时间的快变函数，通常是周期函数或称周期系数。因为系数参数的变化(称为内激励)而引起的振动称为参数激励。当参数激励远离系统的自然频率时，也有可能产生大的响应，称为参数共振。有的系统当参数激励频率接近于系统自然频率两倍时，尽管激励幅值是小的，但系统的响应是很大的，因而发生参数共振(主参数共振)。可能存在着参数记录频率的一个完整的区域，该区域对应于参数共振，所以研究参数激励系统的稳定性是一个很重要的问题。

对于参数激励方程，它的解也许是有界或是无界的，其它部分是稳定的或是不稳定的，都取决于方程里的参数，所以对于方程里面参数的研究从而形成稳定性参数区域分布图。这种理论主要是在参数空间内将参数激励方程的稳定性区域分成稳定和非稳定两个部分。当然穿越稳定边界必然会有一个稳定到非稳定的过渡，且在边界上也有可能存在稳定周期解。一般情况下，通过持续的寻求合适的参数可能得到一个周期性的数值解。

本发明与现有技术相比的优点在于：

(1)本发明利用谐振式陀螺动态特性微分方程得到稳定性参数区域分布图，不需要建立参数检测系统分析参数的稳定性分布，具有分析简单、有效的特点。

(2)本发明对谐振式陀螺稳定性工作的参数取值范围进行了直接界定，减小了参数取值过程中其它优化处理步骤，有效地简化了设计步骤。

附图说明

图1为本发明的谐振式陀螺稳定性分析方法实现过程的示意图；

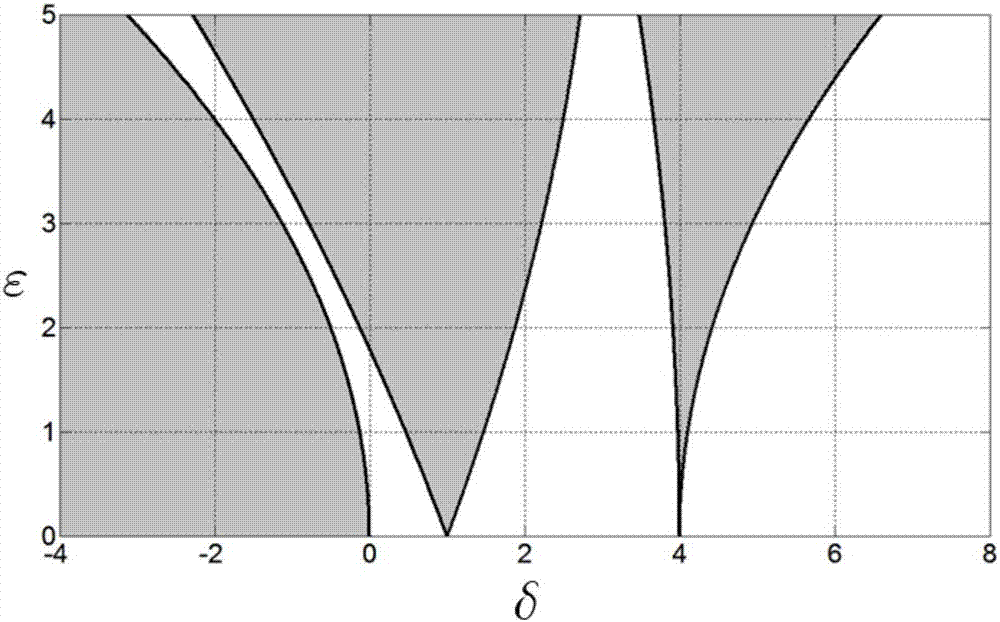
图2为本发明的谐振式陀螺稳定性参数区域分布图。

具体实施方式

下面结合附图以及具体实施方式进一步说明本发明。

本发明谐振式陀螺稳定性分析方法包括以下三个基本步骤：(1)建立谐振式陀螺的动力学模型；(2)绘出谐振式陀螺的稳定性参数区域分布图；(3)确定谐振式陀螺的稳定性参数取值范围。谐振式陀螺动力学模型的系数是时间的快变函数，此种由参数变化引起的振动称为参数激励特征方程。该谐振式陀螺的稳定性分析方法是依据其动力学模型，利用小参数法得到陀螺的稳定性参数区域分布图；构建谐振式陀螺动力学模型的lyapunov函数，从而得到谐振式陀螺的稳定性参数取值范围。本发明克服了参数激励对陀螺输出信号的影响，实现了谐振式陀螺的稳定性工作，拓展其应用范围，也可用于其它谐振式传感器的稳定性分析。

如图1所示，本发明谐振式陀螺稳定性分析方法具体实现步骤如下：

(1)建立动力学模型

谐振式陀螺谐振子的谐振频率是轴向张力的函数，对于直接输出频率这样一种特殊的工作方式，科氏力是随时间变化的动态力，被测量对系统的调制表现为弹性系数的改变，在建立微分方程时就需要利用这样一个假设：轴向力随时间变化是缓慢的，即考虑科氏力的动态响应问题。谐振式陀螺动力学微分方程精确的表征了所有动态特性，最简化的动力学微分方程：

其中，m表示谐振子的质量，x表示谐振子的振幅，k表示谐振子的刚度；实际上，谐振式陀螺的动力学微分方程是一个参数激励振动系统的运动微分方程，将上述方程里的系数展开后的表达式为：

其中，q表示谐振子的振动位移，z是一个时间变量，k＝δ+εcos2z表示谐振子的振动刚度，它随着科氏力作用的变化而变化。当谐振子质量保持不变时，致使谐振子谐振频率发生变化。参数δ表示谐振子自身的固有频率，参数ε可以看作与谐振式陀螺参数相关的一个常量，扰动项εcos2z表示在质量块驱动的作用下对谐振子的弹性系数的调制。

(2)获得稳定性参数区域分布图

谐振式陀螺的动力学微分方程中含有参数δ，把参数δ固定在某些值附件，在参数平面(δ,ε)上研究方程解的稳定性区域。应用非线性振动的小参数法求解，具体方法如下：

把方程(2)的解和参数δ展开为小参数ε的幂级数。

式中ε为小参数也满足陀螺的物理意义，q0，q1，q2分别表示谐振子振动位移的零阶，一阶和二阶扰动量，δ0，δ1，δ2分别表示谐振子自身的固有频率的零阶，一阶和二阶扰动量。

a)设δ0＝0(即n＝0)

可以得到从δ0＝0开始的分界线分别为：

其中，a为固定参数，o(ε³)为参数ε的三阶扰动量参数。

b)设δ0＝1(即n＝1)

可以得到从δ0＝1开始的两条分界线分别为：

它们分别对应与周期为π的周期解：

其中，a和b为固定参数，o(ε³)为参数ε的三阶扰动量参数。

c)设δ0＝4(即n＝2)

可以得到从δ0＝4开始的两条分界线分别为：

它们分别对应与周期为π的周期解：

其中，a和b为固定参数，o(ε³)为参数ε的三阶扰动量参数。以上讨论的结果，如图2所示，图中阴影部分是不稳定区域，其余为稳定区域。随着参数δ的增加，稳定区域越来越大。对于实际工程问题而言，分界线上周期解的稳定性并不重要，因为我们总是要求系统在原理稳定区中运动。但系统的参数落入不稳定区域时，即发生了参数共振。从图2中可见，发生参数共振的区域是一个连续的参数区间。从某种意义上说，避开参数共振比避开因受迫振动而产生的共振要困难的多。

(3)确定稳定性参数取值范围

使得谐振式陀螺的动力学微分方程有稳定性解，利用周期性的lyapunov函数即可确定一个陀螺的参数取值范围。

取q＝q1，谐振式陀螺的动力学微分方程可以写成：

构建lyapunov函数：

对式(11)微分，同时代入式(9)和(10)，则有：

从上式可以看出，只有当时才能半负定，此时q1≡0，不难得出当q1≡0时，q2也为零。所以如果要半负定，即要求：

本发明未详细阐述部分属于本领域技术人员的公知技术。

提供以上实施例仅仅是为了描述本发明的目的，而并非要限制本发明的范围。本发明的范围由所附权利要求限定。不脱离本发明的精神和原理而做出的各种等同替换和修改，均应涵盖在本发明的范围之内。