一种基于Hamming公式预测铣削稳定性的方法与流程

本发明属于先进制造技术领域，尤其涉及一种基于线性多步法中运用Hamming公式预测铣削稳定性的方法，主要用于选择合理的切削参数用来加工零件。

背景技术：

随着现代工业的飞速发展，航空、航天、船舶及汽车等领域对零件的复杂程度越来越高，表面质量要求越严格，对于数控加工能力要求也大幅提高，高速切削加工技术应运而生。但其加工参数的选择和零件本身密切相关，同时受切削过程的影响。有时切削参数的选择过于保守，使得机床难以充分发挥其性能；同时加工参数选择不当，常常导致切削过程失稳，发生颤振等现象，易引起加工缺陷或设备故障，并且加速刀具磨损，严重制约了我国制造业的发展。然而，不同的加工条件下，造成颤振的因素会发生很大的变化，需要准确地避免颤振的发生是非常重要的。铣削加工动力学模型和加工过程稳定域的分析有助于提高加工参数的优选、加工精度和切削效率，进而实现高端数控设备的高性能加工，因此对加工稳定域的准确预测很有必要。

技术实现要素：

为了解决传统预测铣削稳定性的计算方法存在的问题，本发明提出了一种基于线性多步法中运用Hamming公式预测铣削稳定性的方法，从而提高计算效率和计算精度，实现高速精密切削加工。

为了解决上述技术问题，本发明采用如下技术方案：

一种基于Hamming公式预测铣削稳定性的方法，其特征是运用Hamming公式将强迫振动周期离散成间隔相等小区间从而得到铣削系统的传递矩阵，通过Floquet理论判定铣削系统传递矩阵的特征值预测铣削系统的稳定性，从而提高计算效率和计算精度，为加工制造技术人员选择合理的切削参数来提高零件的表面质量提供理论支撑。

运用Hamming公式预测铣削稳定性方法的步骤如下：

步骤1)：建立考虑再生颤振的系统动力学模型：

式(1)中，M、C和K分别为刀具的模态质量矩阵、模态阻尼矩阵和模态刚度矩阵；q(t)为刀具模态坐标；K_c(t)为周期系数矩阵，且K_c(t)＝K_c(t+T)；T为时滞量且等于刀齿切削周期，即T＝60/(NΩ)，且N为刀具齿数，Ω为主轴转速，单位为rpm。

令和通过变换，式(1)可以转换为如下空间状态形式：

式(2)中，A₀表示系统时不变常数矩阵；A(t)表示周期为T的考虑再生效应的系数矩阵，且A(t)＝A(t+T)。

其中:

步骤2)：假设初始时间(刀齿没有加工时的时间)为t₀,刀齿切削周期T可以分为自由振动时间间隔t_f和强迫振动时间间隔T-t_f。

当刀具处于自由振动时刻时，即t∈[t₀,t₀+t_f]，状态值有如下关系：

加工时刀具处于强迫振动时刻，即t∈[t₀+t_f,T]，将切削时间T-t_f平均分成m个时间间隔，则每个时间间隔可表示为h＝T-t_f/m。对于强迫振动的切削时间，相应的离散点可以表示为：

t_i＝t₀+t_f+(i-1)h,i＝1,2,…,m+1 (5)

当t∈[t_i,t_i+1]时，方程(2)可以转化为如下表达式：

步骤3)：将离散点x(t_i)(i＝1,2,…,m+1)通过构造线性多步法来进行求解。由于Hamming公式需要已知三个量来进行表示，所以将x(t_i)(i＝1,2,3)用其他方法计算出来，而对于x(t_i)(i＝4,5,…,m+1)则用Hamming公式计算。

t＝t₁时，代入(6)式可得状态量x(t₁)和时滞量x(t_m+1-T)之间的关系如下式表示：

x(t₂)和x(t₃)通过Adams线性多步法可以表示为：

上式(8)、(9)分别化简可得：

对于x(t_i)(i＝4,5,…,m+1)，运用本说明提出的线性多步法中Hamming公式来进行求解，则可表示为：

上式(12)整理可得：

步骤4)：构建系统的传递矩阵。

将式(7)(10)(11)(13)联立可得：

其中：

其中：G(t_i-2)＝0,

求得的系统的传递矩阵为：

Φ＝P^-1Q (17)

步骤5)：计算系统传递矩阵特征值的模，根据Floquet理论判定铣削系统的稳定系。其判定准则如下：

本发明所述的一种基于线性多步法中运用Hamming公式预测铣削稳定性的方法，根据系统的自由度一般可以分为两种情况：

第一种情况：单自由度系统，其模型可由下列方程表示：

上式(18)中，m_t为刀具的模态质量，单位为kg；ζ为刀具的自然圆频率，单位为rad/s；ω_n为阻尼比；a_p为轴向切削深度，单位为m；T为时滞量，单位为s，即T＝60/(NΩ)。

h(t)为切削力系数，可由下列方程表示：

上式(19)中，K_t、K_n分别为切向和法向切削力系数；φ_j(t)为第j个刀齿的位置角，且N为刀具齿数，Ω为主轴转速(rpm)。

φ_j(t)函数定义为：

式(20)中，φ_st和φ_ex分别表示刀具的切入角和切出角。对于顺铣，φ_st＝arccos(2a/D-1)，φ_ex＝π；逆铣时，φ_st＝0，φ_ex＝arccos(1-2a/D)，其中a/D表示为径向切深与刀具直径之比。

令通过变换，则式(18)可改写为：

上式(21)中，矩阵A₀、A(t)分别为：

第二种情况：两自由度系统，其模型可由下列方程表示：

上式(23)中周期系数矩阵K_c(t)可表示为：

其中：

式(24)-(28)中两自由度系统模型中相关参数与单自由度相同。令通过矩阵变换，则式(23)可改写为：

其中：

本发明在给定主轴转速Ω下，就可获得传递矩阵最大特征值模为1的轴向切削深度。这样，一系列的主轴转速所对应的临界轴向切削深度就构成了铣削系统的稳定域，即稳定性叶瓣图。通过算法计算出来的稳定域，进而选择合理的主轴转速和轴向切削深度，从而避免铣削加工时机床的振动现象，获得较高的表面质量，提高加工效益。

附图说明

图1为本发明为单自由度时浸入比为0.05时的稳定性叶瓣图；

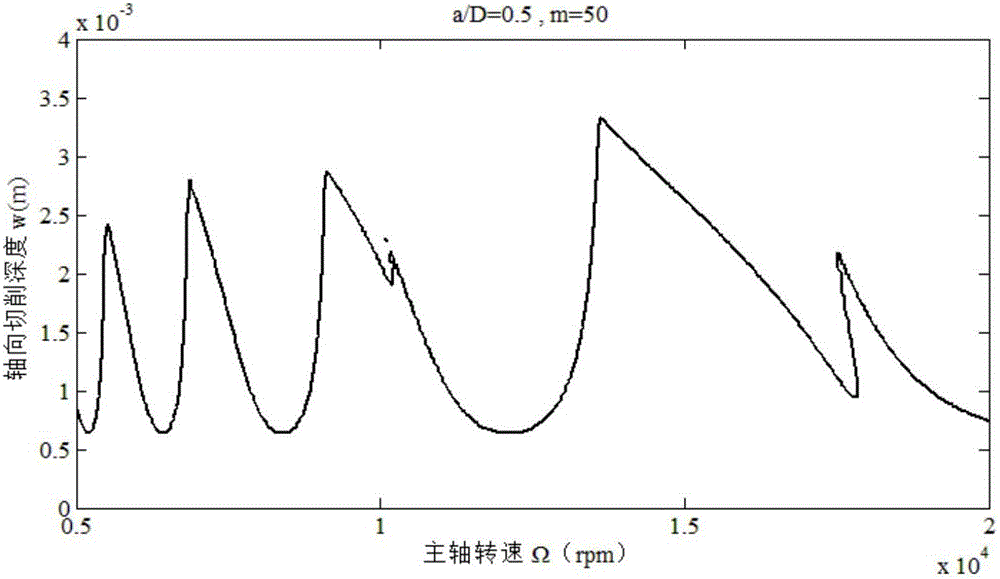
图2为本发明为单自由度时浸入比为0.5时的稳定性叶瓣图；

图3为本发明为单自由度时浸入比为1时的稳定性叶瓣图；

图4为本发明为两自由度时浸入比为0.05时的稳定性叶瓣图；

图5为本发明为两自由度时浸入比为0.5时的稳定性叶瓣图；

图6为本发明为两自由度时浸入比为1时的稳定性叶瓣图；

图7是本发明工艺流程图。

具体实施方式

为了使本发明更加清楚明白，对本发明进行进一步详细描述。应当理解，此处所描述的具体实施例仅用于解释本发明，并不用于限定本发明。

相反，本发明涵盖任何由权利要求定义的在本发明的精髓和范围上做的替代、修改、等效方法以及方案。进一步，为了使公众对本发明有更好的了解，在下文对本发明的细节描述中，详尽描述了一些特定的细节部分。对本领域技术人员来说没有这些细节部分的描述也可以完全理解本发明。

所述的计算方法包括以下步骤：

步骤1)：建立考虑再生颤振的系统动力学模型：

式(1)中，M、C和K分别为刀具的模态质量矩阵、模态阻尼矩阵和模态刚度矩阵；q(t)为刀具模态坐标；K_c(t)为周期系数矩阵，且K_c(t)＝K_c(t+T)；T为时滞量且等于刀齿切削周期，即T＝60/(NΩ)，且N为刀具齿数，Ω为主轴转速，单位为rpm。

令和通过变换，式(1)可以转换为如下空间状态形式：

式(2)中，A₀表示系统时不变常数矩阵；A(t)表示周期为T的考虑再生效应的系数矩阵，且A(t)＝A(t+T)。

其中:

步骤2)：假设初始切削时间为t₀,刀齿切削周期T可以分为自由振动时间间隔t_f和强迫振动时间间隔T-t_f。

当刀具处于自由振动时刻时，即t∈[t₀,t₀+t_f]，状态值有如下关系：

加工时刀具处于强迫振动时刻，即t∈[t₀+t_f,T]，将切削时间T-t_f平均分成m个时间间隔，则每个时间间隔可表示为h＝T-t_f/m。对于强迫振动的切削时间，相应的离散点可以表示为：

t_i＝t₀+t_f+(i-1)h,i＝1,2,…,m+1 (5)

当t∈[t_i,t_i+1]时，方程(2)可以转化为如下表达式：

步骤3)：将离散点x(t_i)(i＝1,2,…,m+1)通过构造线性多步法来进行求解。由于Hamming公式需要已知三个量来进行表示，所以将x(t_i)(i＝1,2,3)用其他方法计算出来，而对于x(t_i)(i＝4,5,…,m+1)则用Hamming公式计算，其计算过程如下。

t＝t₁时，代入(6)式可得状态量x(t₁)和时滞量x(t_m+1-T)之间的关系如下式表示：

x(t₂)和x(t₃)通过Adams线性多步法可以表示为：

上式(8)、(9)分别化简可得：

对于x(t_i)(i＝4,5,…,m+1)，运用本说明提出的线性多步法中Hamming公式来进行求解，则可表示为：

上式(12)整理可得：

步骤4)：构建系统的传递矩阵。

将式(7)(10)(11)(13)联立可得：

其中：

其中：G(t_i-2)＝0,

求得的系统的传递矩阵为：

Φ＝P^-1Q (17)

步骤5)：计算系统传递矩阵特征值的模，根据Floquet理论判定铣削系统的稳定系。其判定准则如下：

本发明所述的一种基于线性多步法中运用Hamming公式预测铣削稳定性的方法，根据系统的自由度一般可以分为两种情况：

第一种情况：单自由度系统，其模型可由下列方程表示：

上式(18)中，m_t为刀具的模态质量，单位为kg；ζ为刀具的自然圆频率，单位为rad/s；ω_n为阻尼比；a_p为轴向切削深度，单位为m；T为时滞量，单位为s，即T＝60/(NΩ)。

h(t)为切削力系数，可由下列方程表示：

上式(19)中，K_t、K_n分别为切向和法向切削力系数；φ_j(t)为第j个刀齿的位置角，且N为刀具齿数，Ω为主轴转速(rpm)。

φ_j(t)函数定义为：

式(20)中，φ_st和φ_ex分别表示刀具的切入角和切出角。对于顺铣，φ_st＝arccos(2a/D-1)，φ_ex＝π；逆铣时，φ_st＝0，φ_ex＝arccos(1-2a/D)，其中a/D表示为径向切深与刀具直径之比。

令通过变换，则式(18)可改写为：

上式(21)中，矩阵A₀、A(t)分别为：

第二种情况：两自由度系统，其模型可由下列方程表示：

上式(23)中周期系数矩阵K_c(t)可表示为：

其中：

式(24)-(28)中两自由度系统模型中相关参数与单自由度相同。令通过矩阵变换，则式(23)可改写为：

其中：

对于单自由度和两自由度，给定相同的参数：逆铣加工，刀具齿数N＝2，模态质量m_t＝0.03993kg，固有圆频率w_n＝922×2πrad/s，固有阻尼ζ＝0.011，切向力系数K_t＝6×10⁸N/m²，法向力系数K_n＝2×10⁸N/m²。将强迫振动周期离散为30小区间，将由主轴转速与径向切削深度构成的平面划分为200×100的网格。

将上述步骤和参数通过Matlab软件进行编程画出稳定性叶瓣图图，通过稳定性叶瓣图来预测铣削过程中的稳定性，选取的径向浸入比分别为0.05、0.5、1，得到单自由度稳定性叶瓣图如图1、2、3所示，两自由度稳定性叶瓣图如图4、5、6所示，Hamming方法预测铣削稳定性叶瓣图流程图如图7所示。