基于非线性模型预测控制的双足机器人步态优化的信赖域‑SQP方法与流程

本发明涉及一种双足机器人领域的步态优化控制方法，具体涉及一种基于非线性模型预测控制的双足机器人步态优化的信赖域-SQP方法。

技术背景

近年来，越来越多的国家将机器人研究纳入国家发展计划，美国《先进制造业国家战略计划》、欧盟SPARC民用机器人研发计划、《中国制造2025》、日本《机器人新战略》、韩国《机器人未来战略2022》等纷纷将机器人发展纳入国家科技创新和产业发展的重点研究领域。机器人已然成为新一轮科技革命与产业变革背景下世界各国产业竞争的焦点。在新科技革命和产业革命的交汇点上，以机器人科技为代表的一类智能产业蓬勃兴起，成为当今时代科技创新的一个重要标志。在分析和借鉴人类行走特性基础上，研究者们已经研制并开发出多款更趋合理完善的双足机器人。随着原型机结构与运行环境工况的复杂性不断提高，给系统控制结构与算法综合提出了更高的要求，特别是有关步态优化控制问题给研究者们提出了新的挑战。

目前用于步态优化控制的方法主要包括如下几类。例如，动态平衡控制理论、基于SLIP(Spring load inverted pendulum)模型的步态优化控制理论、基于仿生学的优化控制理论、时间放缩控制理论、几何规约控制理论、混合零动态控制理论以及离散力学与优化控制理论等等。上述步态优化控制理论有其各自的优缺点。例如，基于仿生学的优化控制理论不仅需要进行大量的实验研究，从仿生学角度设计的控制方法还要用到现实中人的动作数据或者生物学结构，但是，被测试者的身体质量分布和几何尺寸与双足机器人略有差别，从而，导致人与机器人的动力学-运动学数学模型存在很大的差别，把该方法直接应用到实际机器人系统控制过程中，可导致系统存在偏差，因此，破坏了机器人的动态稳定行走。基于混合零动态思想设计的控制器虽然实现了双足机器人的动态稳定行走，但是该方法需要预先已知双足机器人精确的动力学数学模型，否则，该方法便会失效，从而，导致机器人不可能实现稳定的周期运动。利用离散力学与优化控制理论可以实现双足机器人的动态稳定行走，但是，对于变化工况条件下，该方法不能够对机器人系统进行实时控制。然而，非线性模型预测控制技术作为一种用于实时预测与控制方法，具有较强的鲁棒性和 适应性，其能够解决现有控制方法不具备实时性的问题。但是，采用非线性模型预测控制技术离散非线性动力学模型时，时常把动力学模型转化为非凸优化问题，提高了算法的计算复杂度，因此，给系统的实时控制带来了巨大的挑战。

综上所述，现有的步态优化控制方法难以保证控制器对双足机器人系统的实时控制，因而无法实现高效的、稳定的类人行走步态。

技术实现要素：

本发明针对现有技术存在的上述不足，提出一类具有快速收敛特性的信赖域-SQP算法求解双足机器人步态优化问题，算法的设计满足了实际被控系统对控制器的实时性要求，提高了双足机器人步态优化效率。

在此基础上，本发明提出一类具有快速收敛特性的信赖域-SQP算法，利用计算机的编写程序控制整个动态行走过程，具体步骤描述如下：

步骤一，建立一类Compass-like双足机器人动力学数学模型，并且分析双足机器人的运动步态；

步骤二，利用非线性模型预测控制技术，把Compass-like双足机器人的动力学数学模型转化为带有约束条件的非线性优化数学模型；

步骤三，建立一类具有超线性收敛特性的信赖域-SQP算法，求解Compass-like双足机器人的最优控制；

步骤四，利用Compass-like双足机器人进行数值模拟，检验提出算法的可行性和有效性。

建立Compass-like双足机器人动力学数学模型：

步骤一，Compass-Like双足机器人摆动阶段的Lagrangian数学模型

其中，q＝(θ_ns(t),θ_s(t))，θ_ns(t)和θ_s(t)分别代表摆动腿和支撑腿与竖直方向的角位移，代表摆动腿和支撑腿的角速度，代表系统动能，V(q)代表系统势能。同时对(1)求导

因此，摆动阶段的动力学方程为

其中，u＝[u_ns,u_s]^T为控制力矩。如果双足机器人为完全被动行走机器人，那么控制力矩为u＝[0,0]^T。M(q)∈R^2×2为系统的惯性矩阵，为离心力和哥氏力矩阵，G(q)∈R^2×1为重力矩阵。

步骤二，利用角动量守恒定理，Compass-Like双足机器人碰撞切换阶段的代数映射方程

上角标“-”与“+”分别代表碰撞前、后时刻，其中

步骤三，结合摆动阶段和碰撞阶段的数学模型，把它们转化为如下状态空间模型。

定义状态变量为得到如下脉冲混合动力系统：

其中，摆动阶段状态空间，S是碰撞曲面，Δ为碰撞映射。

为方便，(5)写成如下脉冲混合动力系统

其中，和

分析步骤一所述的Compass-like双足机器人的运动步态：

阶段I，支撑腿触地，摆动腿向前摆动。

阶段II，摆动腿摆动至前方最大位置处。

阶段III，由于重力作用，摆动腿向回摆动。

阶段IV，摆动腿与地面碰撞，机器人双腿速度发生突变，并进行状态切换(碰撞前的摆动腿变为支撑腿，碰撞前的支撑腿变成摆动腿)。

利用非线性模型预测控制技术，把Compass-like双足机器人的动力学数学模型转化为带有约束条件的非线性优化数学模型：

步骤一，利用非线性模型预测控制技术，结合四阶龙格-库塔方法把双足机器人的动力学数学模型转化为如下形式的非线性优化模型。

其中，a^k≤b^k∈R^m，Q,P,R是正定矩阵。

步骤二，为方便把(7)转化为如下非线性优化数学模型。

s.t.q＝Φ(q,u)

其中u∈[a,b]

u＝[u⁰；u¹；…,u^N-1],a＝[a⁰；a¹；…,a^N-1],b＝[b⁰；b¹；…,b^N-1]

和

也即是，(8)转化为如下标准的非线性约束优化数学模型。

s.t.g_j(x)≤0,j∈Ω＝{1,2,…,M}

…………(9)

其中，M为约束条件数。

提出一类具有超线性收敛特性的信赖域-SQP算法：

步骤一，数据初始化。假定如下参量取值范围如下：

ρ＞0,δ＞2,θ∈(0,1),v∈(0,1)

和

x⁰∈X,H₀＝I∈R^n×n,η₀＝ρ,η₁＝0.1,η₂＝0.9,0＜θ₁＜1＜θ₂

其中X为迭代点的可行集。

步骤二，计算基本搜索方向通过求解如下形式的QP子问题求解KKT点。

如果则算法停止；如果则算法转入步骤三，否则，进入步骤四。

步骤三，信赖域试探步搜索。计算实际下降量，预优下降量和比率，其中，

实际下降量：

预优下降量：

比率：

如果r_k＞η₁，则令d_k＝0，转入步骤五，否则转入步骤四。

步骤四，按照如下步骤计算可行下降方向。

步骤A，利用如下线性等式系统，计算可行方向

其中

和

步骤B，根据基本搜索方向和下降方向，结合凸组合性质，计算如下形式的可行下降方向d^k，

其中

如果||d^k||≤Δ_k，转入步骤五，否则，令转入步骤五。

步骤五，更新迭代点。按照如下计算公式更新迭代点。

再令k:＝k+1，返回步骤二。

检验提出信赖域-SQP算法的可行性和有效性。

步骤一，选取如下Compass-like双足机器人的物理参数

m＝2kg,M＝10kg,a＝b＝0.5,L＝1m,g＝9.8N/kg,α＝0.5rad,h＝0.1。

步骤二，选取信赖域-SQP算法所需要的参数

ρ＝1,v＝0.5,δ＝2.5,θ＝0.5,η₁＝0.1,η₂＝0.9,θ₁＝0.5,θ₂＝2。

步骤三，利用非线性模型预测控制技术，令N＝2，因此，算法所需要的初始点选取为

q⁰＝[-0.3234 0.2186 -0.3379 -0.0922 -0.3401 0.1268 -0.0023 -0.7515 -0.3283 0.0647 0.2305 -0.4977]和

u⁰＝[0.01 0.02]。

P、Q、R均取相应阶数的单位矩阵。

与现有技术相比，本发明的优点和效果在于利用非线性模型预测控制技术，提出了一类具有超线性收敛特性的信赖域-SQP算法，实时求解双足机器人的最优控制输入，实现双足机器人高效的、稳定的类人行走步态。

本发明所提供的技术方案的积极效果是：

利用非线性模型预测控制技术求解双足机器人的最优控制输入与目前通用的控制输

入求解方法相比，它满足了双足机器人系统对控制器的实时性要求，而且计算简单，容易实现。

本发明提出的一类具有超线性收敛特性的信赖域-SQP算法包括三个循环体。它与传

统信赖域-SQP算法相比，扩大了下一次迭代点的接受范围，并且，当QP子问题不相容时，利用信赖域试探步搜索技术，无需重新求解QP子问题，提高了算法的计算效率。

利用凸组合技术，结合基本搜索方向和可行方向，设计可行下降方向。可行方向的

求解只需求解一个线性系统，与目前通用的QP子问题求解相比，本发明提出 的可行方向求解方法简单易行。并且，搜索方向的可行下降性分析不依赖于任何线搜索准则条件，大大提高了算法的计算效率。

本发明的信赖域-SQP算法的时间复杂度要低于目前已有的算法。在求解可行方向、

下降方向、高阶校正方向的过程中，目前通用的方法一般都是采用求解相应方向的二次规划子问题，然而，本发明采用求解一个二次规划子问题和线性系统以及凸组合的形式大大降低了算法的时间复杂度，从而，提高了算法的计算效率。

总而言之，本发明在保证了快速求解最优控制输入的情况下，有效提高了双足机器人系

统的实时性，实现了双足机器人的步态优化控制。

附图说明

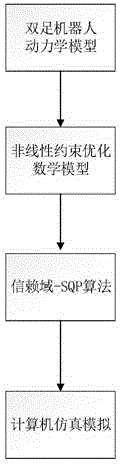
图1为本发明的工作流程框图；

图2为Compass-like双足机器人；

图3为Compass-like双足机器人的行走周期步态；

图4为信赖域-SQP算法流程图；

图5为Compass-like双足机器人闭环控制系统原理图；

图6为关节角与时间函数曲线关系图；

图7为Compass-like双足机器人的角位移与角速度形成的极限环；

图8为摆动腿与地面高度和时间的函数曲线关系图；

图9为Compass-like双足机器人的行走棍图；

具体实施方式

1.参阅图1、图2、图3、图4、图5、图6、图7、图8和图9，本具体实施方式提供一种基于非线性模型预测控制的双足机器人步态优化的信赖域-SQP方法，具体步骤描述如下：

1)建立Compass-like双足机器人动力学数学模型：

Compass-Like双足机器人摆动阶段的Lagrangian数学模型

其中，q=(θ_ns(t),θ_s(t))，θ_ns(t)和θ_s(t)分别代表摆动腿和支撑腿与竖直方向的角位移，代表摆动腿和支撑腿的角速度，代表系统动能，V(q)代表系统势能。同时对(1)求导

因此，摆动阶段的动力学方程为

其中，u＝[u_ns,u_s]^T为控制力矩。如果双足机器人为完全被动行走机器人，那么控制力矩为u=[0,0]^T。M(q)∈R^2×2为系统的惯性矩阵，为离心力和哥氏力矩阵，G(q)∈R^2×1为重力矩阵。

利用角动量守恒定理，Compass-Like双足机器人碰撞切换阶段的代数映射方程

上角标“-”与“+”分别代表碰撞前、后时刻，其中

结合摆动阶段和碰撞阶段的数学模型，把它们转化为如下状态空间模型。

定义可以得到如下脉冲混合动力系统：

其中，摆动阶段状态空间，S是碰撞曲面，Δ为碰撞映射。

为方便，(5)写成如下脉冲混合动力系统

其中，和

2)分析Compass-like双足机器人的运动步态：

阶段I，支撑腿触地，摆动腿向前摆动。

阶段II，摆动腿摆动至前方最大位置处。

阶段III，由于重力作用，摆动腿向回摆动。

阶段IV，摆动腿与地面碰撞，机器人双腿速度发生突变，并进行状态切换(碰撞前的摆动腿变为支撑腿，碰撞前的支撑腿变成摆动腿)。

3)利用非线性模型预测控制技术，结合四阶龙格-库塔方法把双足机器人的动力学数学模型转化为如下形式的非线性优化模型。

其中，a^k≤b^k∈R^m，Q,P,R是正定矩阵。

为方便把(7)通过等价转化的形式，转化为如下非线性优化数学模型。

s.t.q＝Φ(q,u)

其中u∈[a,b]

u＝[u⁰；u¹；…,u^N-1],a＝[a⁰；a¹；…,a^N-1],b＝[b⁰；b¹；…,b^N-1]

和

也即是，(8)转化为如下标准的非线性约束优化数学模型。

其中，M为约束条件数。

4)提出一类具有超线性收敛特性的信赖域-SQP算法：

步骤一，数据初始化。假定如下参量取值范围如下：

ρ＞0,δ＞2,θ∈(0,1),v∈(0,1)

和

x⁰∈X,H₀＝I∈R^n×n,η₀＝ρ,η₁=0.1,η₂＝0.9,0＜θ₁＜1＜θ₂

其中X为迭代点的可行集。

步骤二，计算基本搜索方向通过求解如下形式的QP子问题求解KKT点。

如果则算法停止；如果则算法转入步骤三，否则，进入步骤四。

步骤三，信赖域试探步搜索，计算实际下降量，预优下降量和比率，其中，实际下降量：

预优下降量：

比率：

如果r_k＞η₁，则令d_k=0，转入步骤五，否则转入步骤四。

步骤四，按照如下步骤计算可行下降方向。

步骤A，利用如下线性等式系统，计算可行方向

其中

和

步骤B，根据基本搜索方向和下降方向，结合凸组合性质，计算如下形式的可行下降方向d^k，

其中

如果||d^k||≤Δ_k，转入步骤五，否则，令转入步骤五。

步骤五，更新迭代点。按照如下计算公式更新迭代点。

再令k:＝k+1，返回步骤二。

5)检验提出信赖域-SQP算法的可行性和有效性。

选取如下Compass-like双足机器人的物理参数

m＝2kg,M＝10kg,a＝b＝0.5,L＝1m,g＝9.8N/kg,α＝0.5rad,h＝0.1。

选取信赖域-SQP算法所需要的参数

ρ＝1,v＝0.5,δ＝2.5,θ＝0.5,η₁＝0.1,η₂＝0.9,θ₁＝0.5,θ₂＝2。

利用非线性模型预测控制技术，令N＝2，因此，算法所需要的初始点选取为

q⁰＝[-0.3234 0.2186 -0.3379 -0.0922 -0.3401 0.1268 -0.0023 -0.7515 -0.3283 0.0647 0.2305 -0.4977]和

u⁰＝[0.01 0.02]。

P、Q、R均取相应阶数的单位矩阵。

本发明是一种基于非线性模型预测控制技术的双足机器人步态优化控制方法,以一个Compass-like双足机器人实施例并结合附图说明及具体操作步骤如下：

1)在算法实施例中，我们选择较为简单的Compass-like双足机器人作为实施例对象，具体见图[2]。虽然结构简单，但是，可以充分说明我们提出算法的可行性和有效性，并且，可以通过对本发明做适当的修改，便可把本发明推广到多自由度的双足机器人，因此，不会影响本发明的适用范围。利用Lagrangian原理和角动量守恒条件，建立Compass-like双足机器人动力学模型，并且通过计算机符号计算表达该类模型，便于算法实现。Compass-Like双足机器人由两条腿构成，上身简化为髋关节点质量。两条腿的长度相同，质量为m，腿长为L＝a+b，其中，a代表腿的质心到腿的末端的长度，b代表腿的质心到髋关节的距离。θ_ns代表摆动腿与竖直方向的夹角，θ_s代表支撑腿与竖直方向的夹角，并且，记逆时针方向为正方向。当摆动腿与地面接触时，两条腿之间的夹角为α。我们选取如下形式的双足机器人的物理参数。

m＝2kg,M＝10kg,a=b＝0.5,L＝1m,α＝0.5rad。

2)利用非线性模型预测控制技术，结合四阶龙格-库塔方法，以低能耗作为性能指标，把Compass-like双足机器人连续的动力学数学模型转化为离散的非线 性优化数学模型，为求解最优控制输入奠定基础。采用四阶龙格-库塔方法离散连续动力学模型过程中，离散步长选取为h＝0.1,并且，模型预测控制中的预测步长选取为N＝2。

3)为了能够很好的实施信赖域-SQP算法，具体见图[4]。我们选取如下参数

ρ＝1,v＝0.5,δ＝2.5,θ＝0.5,η₁＝0.1,η₂＝0.9,θ₁＝0.5,θ₂＝2。

实际上，这些参数不是固定不变的，只要符合本发明提出的信赖域-SQP算法参数选取范围，本算法均为可行的、有效的。只是在计算速度上，会有一定的影响，但是，一般不会出现特别差的情况。

4)为了求解双足机器人的最优控制输入，我们选取非线性优化模型的初始点和初始控制输入分别为

q⁰＝[-0.3234 0.2186 -0.3379 -0.0922 -0.3401 0.1268 -0.0023 -0.7515 -0.3283 0.0647 0.2305 -0.4977]和

u⁰＝[0.01 0.02]。

通过上面两个初始点的选取，本发明提出的信赖域-SQP算法便可以实时求解最优控制输入，再把控制输入带入双足机器人动力学模型中，结合Matlab软件库中的ODE命令，便可求解双足机器人的关节角最优运动轨迹、摆动腿与地面高度变化、极限环以及行走棍图，具体见图[6-9]。

显然，本领域的技术人员可以对本发明进行各种改动和变型而不脱离本发明的精神和范围。例如，可以适当增加双足机器人的关节自由度，把本发明推广到多自由度的双足机器人等等。这样，倘若本发明的这些修改和变型属于本发明权利要求及其等同技术的范围之内，则本发明也意图包含这些改动和变型在内。