一种叶面积指数空间尺度转换方法及装置与流程
本发明涉及信息处理技术领域,更具体地说,涉及一种信息处理方法及装置。
背景技术:
叶面积指数是表征植被结构及其生长状态的关键指标,其在农作物群体长势监测、产量与品质估算、病虫害监测等领域均有着重要且广泛的应用。遥感反演是获取区域农作物叶面积指数的主要途径,其以空间遥感技术获取的宏观区域地物电磁波信息为数据源,通过构建描述地物电磁波与叶面积指数之间相互关系的数学模型,定量反演农作物叶面积指数。随着遥感技术的日益发展,多样化的综合对地观测系统为遥感农作物反演叶面积指数提供了多源化的观测数据集,遥感影像各有自己的分辨率、幅面和波段选择等,充分利用多传感器的互补信息,开展科学合理的多源遥感数据联合应用,有利于提升叶面积指数的反演精度与可靠性。由于地表空间异质性的普遍存在和遥感观测信息多空间分辨率并有的特点,在基于多源遥感观测开展农作物叶面积指数定量反演时,叶面积指数遥感反演模型的非线性必然导致多空间尺度遥感反演叶面积指数结果的不一致,从而产生叶面积指数的空间尺度效应(即在不同的空间尺度下,地表参量表现出的差异或地表过程表现出的不同特征),而空间尺度转换作为空间尺度效应的解决方法得到了国内外研究学者的普遍关注。
目前,最常用的空间尺度转换方法是泰勒级数展开法,泰勒级数展开法是经典的物理类空间尺度转换方法,该方法先对待转换的叶面积指数进行空间尺度变换,得到初始转换结果,然后通过基于泰勒级数展开法确定的校正参数对初始转换结果进行校正得到最终的空间尺度转换结果。基于泰勒级数展开法的空间尺度转换方法能够较为直观地给出叶面积指数遥感反演模型和反演模型驱动变量在叶面积指数空间尺度效应中的具体响应机制与模式,且在小空间尺度遥感观测数据存在的情况下,能够较好地开展不同空间尺度叶面积指数面状信息的转换。而由于泰勒级数展开法的应用前提是叶面积指数 遥感反演模型在地表下垫面内连续且n阶可导,而现实中的地表下垫面大都具有空间异质性,故该方法在实际应用中受到较大的局限。
考虑到农作物叶面积指数空间尺度转换普适性和高精度的应用需求,有必要提供一种使用范围更广的物理类空间尺度转换方法,并能够提高复杂地表下垫面内农作物叶面积指数空间尺度转换的数值精度。
技术实现要素:
本发明的目的是提供一种适用范围更广的叶面积指数空间尺度转换方法及装置,并提高复杂地表下垫面内农作物叶面积指数空间尺度转换的数值精度。
为实现上述目的,本发明提供了如下技术方案:
一种叶面积指数空间尺度转换方法,包括:
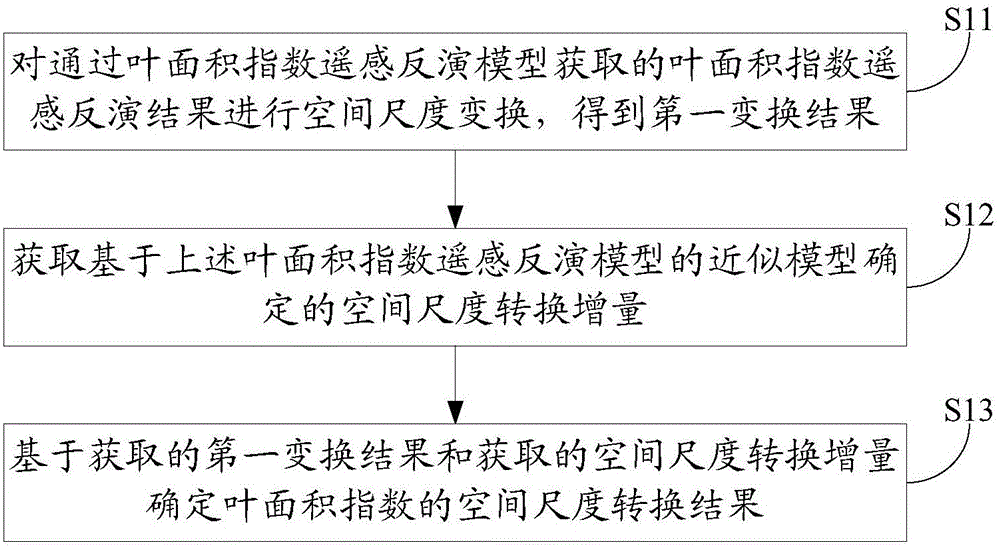
对通过叶面积指数遥感反演模型获取的叶面积指数进行空间尺度变换,得到第一变换结果;
获取基于所述叶面积指数遥感反演模型的近似模型确定的空间尺度转换增量,所述近似模型为:基于切比雪夫多项式构建的所述叶面积指数遥感反演模型的最佳平方逼近n次多项式;
基于所述第一变换结果和所述空间尺度转换增量确定所述叶面积指数的空间尺度转换结果。
上述方法,优选的,所述近似模型为:
其中,aj为基于和叶面积指数遥感反演模型确定的计算系数;为基于第一类切比雪夫多项式构建的n个线性无关的正交基函数。
上述方法,优选的,相应的,所述近似模型为:
其中,
Tk(x)为第一类切比雪夫多项式,M(x)为所述叶面积指数遥感反演模型。
上述方法,优选的,所述空间尺度转换增量为:
Δm=g(f(R(p)))-f(g(R(p))),其中,
Δm表示所述空间尺度转换增量;R(p)表示用于获取所述叶面积指数的遥感影像中像素点p的反射率数据;f(·)表示空间尺度变换函数;g(·)表示所述近似模型。
上述方法,优选的,所述基于所述第一变换结果和所述空间尺度转换增量确定所述叶面积指数的空间尺度转换结果包括:
将所述第一变换结果与所述空间尺度转换增量的和值确定为所述叶面积指数遥感反演结果的空间尺度转换结果。
一种叶面积指数空间尺度转换装置,包括:
变换模块,用于对通过叶面积指数遥感反演模型获取的叶面积指数进行空间尺度变换,得到第一变换结果;
获取模块,用于获取基于所述叶面积指数遥感反演模型的近似模型确定的空间尺度转换增量,所述近似模型为:基于切比雪夫多项式构建的所述叶面积指数遥感反演模型的最佳平方逼近n次多项式;
确定模块,用于基于所述第一变换结果和所述空间尺度转换增量确定所述叶面积指数的空间尺度转换结果。
上述装置,优选的,所述近似模型为:
其中,aj为基于和叶面积指数遥感反演模型确定的计算系数;为基于第一类切比雪夫多项式构建的n个线性无关的正交基函数。
上述装置,优选的,相应的,所述近似模型为:
其中,
Tk(x)为第一类切比雪夫多项式,M(x)为所述叶面积指数遥感反演模型。
上述装置,优选的,所述空间尺度转换增量为:
Δm=g(f(R(p)))-f(g(R(p))),其中,
Δm表示所述空间尺度转换增量;R(p)表示用于获取所述叶面积指数的遥感影像中像素点p的反射率数据;f(·)表示空间尺度变换函数;g(·)表示所述近似模型。
上述装置,优选的,所述确定模块包括:
第一确定单元,用于将所述第一变换结果与所述空间尺度转换增量的和值确定为所述叶面积指数遥感反演结果的空间尺度转换结果。
通过以上方案可知,本申请提供的一种叶面积指数空间尺度转换方法及装置,对通过叶面积指数遥感反演模型获取的第一空间分辨率遥感影像的叶面积指数遥感反演结果进行空间尺度变换,得到第一变换结果,获取通过基于切比雪夫多项式构建的近似模型得到的空间尺度转换增量,基于第一变换结果和空间尺度变换增量确定叶面积指数遥感反演结果的空间尺度转换结果。由于近似模型基于切比雪夫多项式构建,因此,近似模型不涉及导数,因此,本发明实施例提供的叶面积指数空间尺度转换方法及装置只要求叶面积指数遥感反演模型在地表下垫面内连续即可,应用范围更广,而且通过实验可以确定,本发明实施例提供的叶面积指数空间尺度转换方法及装置的转换精度较高。
附图说明
为了更清楚地说明本发明实施例或现有技术中的技术方案,下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍,显而易见地,下面描述中的附图仅仅是本发明的一些实施例,对于本领域普通技术人员来讲,在不付出创造性劳动的前提下,还可以根据这些附图获得其他的附图。
图1为本发明实施例提供的叶面积指数空间尺度转换方法的一种实现流程图;
图2为黑河流域盈科绿洲区的小麦多空间尺度遥感观测数据;
图3为河北省粮食主产区的小麦多空间尺度遥感观测数据;
图4a为对图2左图进行升尺度后得到的遥感数据进行叶面积指数遥感反演得到的叶面积指数与由图2左图通过叶面积指数遥感反演得到的叶面积指数进行升尺度得到的叶面积指数的对应关系;
图4b为基于泰勒级数展开法的叶面积指数的空间尺度转换方法得到的叶面积指数与由图2左图通过叶面积指数遥感反演得到的叶面积指数进行升尺度得到的叶面积指数的对应关系;
图4c为基于本发明实施例提供的叶面积空间尺度转换方法得到的叶面积指数与由图2左图通过叶面积指数遥感反演得到的叶面积指数进行升尺度得到的叶面积指数的对应关系;
图5a为对图3左图进行升尺度后得到的遥感数据进行叶面积指数遥感反演得到的叶面积指数与由图3左图通过遥感反演得到的叶面积指数进行升尺度得到的叶面积指数的对应关系;
图5b为基于泰勒级数展开法的叶面积指数的空间尺度转换方法得到的叶面积指数与由图3左图通过叶面积指数遥感反演得到的叶面积指数进行升尺度得到的叶面积指数的对应关系;
图5c为基于本发明实施例提供的叶面积空间尺度转换方法得到的叶面积指数与由图3左图通过叶面积指数遥感反演得到的叶面积指数进行升尺度得到的叶面积指数的对应关系;
图6为本发明实施例提供的叶面积指数空间尺度转换装置的一种结构示意图。
说明书和权利要求书及上述附图中的术语“第一”、“第二”、“第三”“第四”等(如果存在)是用于区别类似的部分,而不必用于描述特定的顺序或先后次序。应该理解这样使用的数据在适当情况下可以互换,以便这里描述的本申请的实施例能够以除了在这里图示的以外的顺序实施。
具体实施方式
下面将结合本发明实施例中的附图,对本发明实施例中的技术方案进行清楚、完整地描述,显然,所描述的实施例仅仅是本发明一部分实施例,而 不是全部的实施例。基于本发明中的实施例,本领域普通技术人员在没有付出创造性劳动前提下所获得的所有其他实施例,都属于本发明保护的范围。
请参阅图1,图1为本发明实施例提供的叶面积指数空间尺度转换方法的一种实现流程图,可以包括:
步骤S11:对通过叶面积指数遥感反演模型获取的叶面积指数遥感反演结果进行空间尺度变换,得到第一变换结果;
在通过叶面积指数遥感反演模型对第一遥感影像进行反演得到叶面积指数后,对得到的叶面积指数进行空间尺度变换,该空间尺度变换可以是升尺度变换算法,也可以是降尺度变换算法。具体可以根据空间尺度变换的目标空间分辨率确定,若目标空间分辨率低于第一遥感影像的空间分辨率,则采用升尺度变换算法对得到的叶面积指数进行空间尺度变换,若目标空间分辨率高于第一遥感影像的空间分辨率,则采用降尺度变换算法对得到的叶面积指数进行空间尺度变换。
假设p为较高空间分辨率遥感影像的像素点,该像素点的反射率值可以表示为(R1(p),R2(p),...,Rn(p));q为较低空间分辨率遥感影像的像素点,该像素点的反射率值可以表示为(R1(q),R2(q),...,Rn(q)),则较高空间分辨率的反射率数据(小尺度数据)通过升尺度算法可以得到较低空间分辨率的反射率数据(大尺度数据)。具体的,较高空间分辨率的反射率数据与较低空间分辨率的反射率数据之间的关系公式可以表示为:
其中,U表示较高空间分辨率数据所表征的研究区域,u表示较高空间分辨率的一个像素点所表征的研究区域,Us表示较低空间分辨率的像素点所表征的研究区域所覆盖的较高空间分辨率的像素点所表征的研究区域U的面积和。
升尺度变换和降尺度变换为逆变换。
假设M(·)为农作物叶面积指数遥感反演模型,其以遥感影像的反射率数据为输入,以农作物叶面积指数为输出。则对较高空间分辨率的叶面积指数M(R1(p),R2(p),...,Rn(p))进行升尺度变换得到较低空间分辨率的叶面积指数M'(R1(p),R2(p),...,Rn(p)),或者,对较低空间分辨率的叶面积指数 M(R1(q),R2(q),...,Rn(q))进行降尺度变换得到较高空间分辨率的叶面积指数M'(R1(q),R2(q),...,Rn(q))。M'(R1(q),R2(q),...,Rn(q))和M'(R1(p),R2(p),...,Rn(p))均属于第一变换结果。
步骤S12:获取基于上述叶面积指数遥感反演模型的近似模型确定的空间尺度转换增量,上述近似模型为:基于切比雪夫多项式构建的上述叶面积指数遥感反演模型的最佳平方逼近n次多项式;
反射率数据的取值范围为[0,1],则对农作物叶面积指数遥感反演模型M(x)而言,存在唯一多项式是M(x)的最佳平方逼近n次多项式,其中,aj为基于和叶面积指数遥感反演模型M(x)确定的计算系数;为n个线性无关的正交基函数。
本发明实施例中,n次多项式g(x)中的线性无关的正交基函数基于切比雪夫多项式构造。
也就是说,本发明实施例中,用n次多项式g(x)近似表示农作物叶面积指数遥感反演模型M(x)。
本发明实施例中,空间尺度增量可能为正数,也可能为负数。
步骤S13:基于获取的第一变换结果和获取的空间尺度转换增量确定叶面积指数的空间尺度转换结果。
本发明实施例中,使用基于切比雪夫多项式确定的空间尺度转换增量对第一变换结果进行校正,得到最终的叶面积指数空间尺度转换结果。
本发明实施例提供的叶面积指数空间尺度转换方法,对通过叶面积指数遥感反演模型获取的第一空间分辨率遥感影像的叶面积指数遥感反演结果进行空间尺度变换,得到第一变换结果,获取通过基于切比雪夫多项式构建的近似模型得到的空间尺度转换增量,基于第一变换结果和空间尺度变换增量确定叶面积指数遥感反演结果的空间尺度转换结果。由于近似模型基于切比雪夫多项式构建,因此,近似模型不涉及导数,因此,本发明实施例提供的叶面积指数空间尺度转换方法只要求叶面积指数遥感反演模型在地表下垫面内连续即可,应用范围更广,而且通过实验可以确定,本发明实施例提供的叶面积指数空间尺度转换方法的转换精度较高。
上述实施例中,可选的,n次多项式g(x)中的线性无关的正交基函数可以基于第一类切比雪夫多项式构造。
第一类切比雪夫多项式为:
可选的,及相应的,上述近似模型可以为:
其中,
Tk(x)为第一类切比雪夫多项式,M(x)为叶面积指数遥感反演模型。
本发明实施例中,基于第一类切比雪夫多项式构造n次多项式g(x)中的线性无关的正交基函数的方式为本发明实施例中不限于这一种构造方式,也可以为基于第一类切比雪夫多项式构造n次多项式g(x)中的线性无关的正交基函数的其它的构造方式,只要为线性无关的正交基函数即可。
可选的,上述空间尺度变换增量可以为:
Δm=g(f(R(p)))-f(g(R(p))) (4)
其中,Δm表示所述空间尺度转换增量;R(p)表示用于获取所述叶面积指数的遥感影像中像素点p的反射率数据;f(·)表示空间尺度变换函数;g(·)表示所述近似模型。
下面举例说明本发明实施例提供的叶面积指数空间尺度转换方法的一种具体实现方式。
假设遥感观测数据为较高空间分辨率遥感影像的各个像素点的反射率值(小尺度数据),该较高空间分辨率遥感影像的像素点p的反射率值为 (R1(p),R2(p),...,Rn(p))。本示例中,要将较高空间分辨率遥感影像的叶面积指数转换到较低空间分辨率下的叶面积指数。具体为:
对遥感观测数据通过叶面积指数遥感反演模型M进行遥感反演,得到叶面积指数M(R1(p),R2(p),...,Rn(p))。
对反演结果M(R1(p),R2(p),...,Rn(p))进行尺度提升,得到升尺度结果M'(R1(p),R2(p),...,Rn(p)),即
获取空间尺度变换增量Δm,
其中,g(·)表示预置的叶面积指数遥感反演模型的近似模型。
则由较高空间分辨率遥感影像的叶面积指数转换得到的较低空间分辨率下的叶面积指数为:
M'(R1(p),R2(p),...,Rn(p))+Δm。
下面说明本示例中,叶面积指数遥感反演模型的近似模型的确定过程:
由于反射率数据的取值范围为[0,1],则对农作物叶面积指数遥感反演模型M(x)而言,存在唯一多项式是M(x)的最佳平方逼近n次多项式,其中,aj为基于和叶面积指数遥感反演模型M(x)确定的计算系数;为线性无关的正交基函数。
本示例中,基于第一类切比雪夫多项式(即公式(2))构造g(x)的正交基函数,具体的,则有,
其中,
Tk(x)为第一类切比雪夫多项式,M(x)为叶面积指数遥感反演模型。
为方便数值计算,本示例中,将g(x)表达式转换为形如的表达形式,由于,
a1T1(x)=a1x
a2T2(x)=a2(2xT1(x)-T0(x))=2a2x2-a2
a3T3(x)=a3(2xT2(x)-T1(x))=4a3x3-2a3x2-2a3x-a3
a4T4(x)=a4(2xT3(x)-T2(x))=8a4x4-8a4x3-6a4x2-4a4x-a4
……
将上述等式右端的项按次幂排于同列(即相同次幂的项排于同一列),然后沿着列相加其系数,则可以得到的表达式,其中bk由上述akTk(x)的展开式确定。
相应的,空间尺度变换增量Δm的确定方式为:
由上述公式(5)可知,由较低空间分辨率的遥感数据进行遥感反演得到的叶面积指数M(R(q))与由较高空间分辨率的叶面积指数进行空间尺度转换得到的叶面积指数M'(R(p))的差异与研究区U内数据的特异性正相关,即,若研究区U内遥感观测数据的空间异质性(由反射率值表征)较大或叶面积指数遥感反演模型的非线性程度(由k值表征)较高,则M(R(q))与M'(R(p))的差异较大。
可见,基于切比雪夫最佳一致逼近法的叶面积指数空间尺度转换方法相对于依据泰勒级数展开法建立的叶面积指数空间尺度转换方法而言,能够更为有效地定量描述遥感观测数据本身和叶面积指数遥感定量反演模型的非线性特征对农作物叶面积指数空间尺度效应的具体贡献和响应机制,进而完成叶面积指数的空间尺度转换。
本发明实施例提供的叶面积指数空间尺度转换方法,不仅具有空间尺度的自适应能力(即,既可以由较高空间尺度向较低空间尺度转换,也可以由 较低空间尺度向较高空间尺度转换),而且适用范围更广,在不同地表复杂度的下垫面内应用的可移植性较强。
下面分别以黑河流域盈科绿洲区(绿洲下垫面:集中连片的农田规模较大,空间分布较为均衡,如图2所示,左图为TM遥感影像数据,空间分辨率为30m(属于较高空间分辨率的反射率数据,即小尺度数据),右图为MODIS遥感影像数据,空间分辨率为500m(属于较低空间分辨率的反射率数据,即大尺度数据))和河北省粮食主产区(华北农田下垫面:集中连片的农田规模较小,空间分布较不均衡,如图3所示,左图为TM遥感影像数据,空间分辨率为30m(属于较高空间分辨率的反射率数据,即小尺度数据),右图为MODIS遥感影像数据,空间分辨率为500m(属于较低空间分辨率的反射率数据,即大尺度数据))获取的小麦多空间尺度遥感观测数据为信息源,对基于泰勒级数展开法的叶面积指数的空间尺度转换方法和基于本发明实施例提供的叶面积指数空间尺度转换方法进行比对。
本示例中,需要对空间分辨率为30m的叶面积指数转换为空间分辨率为500m的叶面积指数。
如图4a-4c所示,为黑河流域盈科绿洲区叶面积指数空间尺度转换结果对比图。其中,图4a为对图2左图进行升尺度后得到的遥感数据进行叶面积指数遥感反演得到的叶面积指数与由图2左图通过叶面积指数遥感反演得到的叶面积指数进行升尺度得到的叶面积指数的对应关系,图4b为基于泰勒级数展开法的叶面积指数的空间尺度转换方法得到的叶面积指数与由图2左图通过叶面积指数遥感反演得到的叶面积指数进行升尺度得到的叶面积指数的对应关系,图4c为基于本发明实施例提供的叶面积空间尺度转换方法得到的叶面积指数与由图2左图通过叶面积指数遥感反演得到的叶面积指数进行升尺度得到的叶面积指数的对应关系。图4a-4c中,虚线为理想情况下,由图2右图通过叶面积指数遥感反演得到的叶面积指数(即实测数据)与由图2左图通过叶面积指数遥感反演得到的叶面积指数进行升尺度得到的叶面积指数的对应关系,即理想情况下,由图2左图通过叶面积指数遥感反演得到的叶面积指数进行升尺度得到的叶面积指数等于实测数据。每个图中的实线为由图中的分布的点拟合得到的直线,显然,基于本发明实施例提供的叶面积空间 尺度转换方法得到的叶面积指数更接近理想情况,本示例中,基于泰勒级数展开法的叶面积指数的空间尺度转换方法得到的叶面积指数比理想情况高11.87%,而基于本发明实施例提供的叶面积空间尺度转换方法得到的叶面积指数只比理想情况高7.26%,精确度比基于泰勒级数展开法的叶面积指数的空间尺度转换方法得到的叶面积指数提高4.61%。
如图5a-5c所示,为河北省粮食主产区叶面积指数空间尺度转换结果对比图。其中,图5a为对图3左图进行升尺度后得到的遥感数据进行叶面积指数遥感反演得到的叶面积指数与由图3左图通过遥感反演得到的叶面积指数进行升尺度得到的叶面积指数的对应关系,图5b为基于泰勒级数展开法的叶面积指数的空间尺度转换方法得到的叶面积指数与由图3左图通过叶面积指数遥感反演得到的叶面积指数进行升尺度得到的叶面积指数的对应关系,图5c为基于本发明实施例提供的叶面积空间尺度转换方法得到的叶面积指数与由图3左图通过叶面积指数遥感反演得到的叶面积指数进行升尺度得到的叶面积指数的对应关系。图5a-5c中,虚线为理想情况下,由图3右图通过叶面积指数遥感反演得到的叶面积指数(即实测数据)与由图3左图通过叶面积指数遥感反演得到的叶面积指数进行升尺度得到的叶面积指数的对应关系,即理想情况下,由图3左图通过叶面积指数遥感反演得到的叶面积指数进行升尺度得到的叶面积指数等于实测数据。每个图中的实线为由图中的分布的点拟合得到的直线,显然,基于本发明实施例提供的叶面积空间尺度转换方法得到的叶面积指数更接近理想情况,本示例中,基于泰勒级数展开法的叶面积指数的空间尺度转换方法得到的叶面积指数比理想情况高9.07%,而基于本发明实施例提供的叶面积空间尺度转换方法得到的叶面积指数只比理想情况高5.63%,精确度比基于泰勒级数展开法的叶面积指数的空间尺度转换方法得到的叶面积指数提高3.44%。
与方法实施例相对应,本发明实施例还提供一种叶面积指数空间尺度转换装置,本发明实施例提供的叶面积指数空间尺度转换装置的一种结构示意图如图6所示,可以包括:
变换模块61,获取模块62和确定模块63;其中,
变换模块61用于对通过叶面积指数遥感反演模型获取的叶面积指数进行空间尺度变换,得到第一变换结果;
在通过叶面积指数遥感反演模型对第一遥感影像进行反演得到叶面积指数后,变换模块对得到的叶面积指数进行空间尺度变换,该空间尺度变换可以是升尺度变换算法,也可以是降尺度变换算法。具体可以根据空间尺度变换的目标空间分辨率确定,若目标空间分辨率低于第一遥感影像的空间分辨率,则采用升尺度变换算法对得到的叶面积指数进行空间尺度变换,若目标空间分辨率高于第一遥感影像的空间分辨率,则采用降尺度变换算法对得到的叶面积指数进行空间尺度变换。
假设p为较高空间分辨率遥感影像的像素点,该像素点的反射率值可以表示为(R1(p),R2(p),...,Rn(p));q为较低空间分辨率遥感影像的像素点,该像素点的反射率值可以表示为(R1(q),R2(q),...,Rn(q)),则较高空间分辨率的反射率数据(小尺度数据)通过升尺度算法可以得到较低空间分辨率的反射率数据(大尺度数据)。具体的,较高空间分辨率的反射率数据与较低空间分辨率的反射率数据之间的关系公式可以表示为:
其中,U表示较高空间分辨率数据所表征的研究区域,u表示较高空间分辨率的一个像素点所表征的研究区域,Us表示较低空间分辨率的像素点所表征的研究区域所覆盖的较高空间分辨率的像素点所表征的研究区域U的面积和。
升尺度变换和降尺度变换为逆变换。
假设M(·)为农作物叶面积指数遥感反演模型,其以遥感影像的反射率数据为输入,以农作物叶面积指数为输出。则对较高空间分辨率的叶面积指数M(R1(p),R2(p),...,Rn(p))进行升尺度变换得到较低空间分辨率的叶面积指数M'(R1(p),R2(p),...,Rn(p)),或者,对较低空间分辨率的叶面积指数M(R1(q),R2(q),...,Rn(q))进行降尺度变换得到较高空间分辨率的叶面积指数M'(R1(q),R2(q),...,Rn(q))。M'(R1(q),R2(q),...,Rn(q))和M'(R1(p),R2(p),...,Rn(p))均属于第一变换结果。
获取模块62用于获取基于上述叶面积指数遥感反演模型的近似模型确定的空间尺度转换增量,上述近似模型为:基于切比雪夫多项式构建的叶面积指数遥感反演模型的最佳平方逼近n次多项式;
反射率数据的取值范围为[0,1],则对农作物叶面积指数遥感反演模型M(x)而言,存在唯一多项式是M(x)的最佳平方逼近n次多项式,其中,aj为基于和叶面积指数遥感反演模型M(x)确定的计算系数;为n个线性无关的正交基函数。
本发明实施例中,n次多项式g(x)中的线性无关的正交基函数基于切比雪夫多项式构造。
也就是说,本发明实施例中,用n次多项式g(x)近似表示农作物叶面积指数遥感反演模型M(x)。
本发明实施例中,空间尺度增量可能为正数,也可能为负数。
确定模块63用于基于得到的第一变换结果和空间尺度转换增量确定获取的叶面积指数的空间尺度转换结果。
本发明实施例提供的叶面积指数空间尺度转换装置,对通过叶面积指数遥感反演模型获取的第一空间分辨率遥感影像的叶面积指数遥感反演结果进行空间尺度变换,得到第一变换结果,获取通过基于切比雪夫多项式构建的近似模型得到的空间尺度转换增量,基于第一变换结果和空间尺度变换增量确定叶面积指数遥感反演结果的空间尺度转换结果。由于近似模型基于切比雪夫多项式构建,因此,近似模型不涉及导数,因此,本发明实施例提供的叶面积指数空间尺度转换装置只要求叶面积指数遥感反演模型在地表下垫面内连续即可,应用范围更广,而且通过实验可以确定,本发明实施例提供的叶面积指数空间尺度转换装置的转换精度较高。
上述实施例中,可选的,n次多项式g(x)中的线性无关的正交基函数可以基于第一类切比雪夫多项式构造。
第一类切比雪夫多项式为:
T0(x)=1
T1(x)=x
Tn+1(x)=2xTn(x)-Tn-1(x),n=1,2,3,...
可选的,及相应的,上述近似模型可以为:
其中,
Tk(x)为第一类切比雪夫多项式,M(x)为叶面积指数遥感反演模型。
本发明实施例中,基于第一类切比雪夫多项式构造n次多项式g(x)中的线性无关的正交基函数的方式为本发明实施例中不限于这一种构造方式,也可以为基于第一类切比雪夫多项式构造n次多项式g(x)中的线性无关的正交基函数的其它的构造方式,只要为线性无关的正交基函数即可。
可选的,上述空间尺度变换增量可以为:
Δm=g(f(R(p)))-f(g(R(p)))
其中,Δm表示所述空间尺度转换增量;R(p)表示用于获取所述叶面积指数的遥感影像中像素点p的反射率数据;f(·)表示空间尺度变换函数;g(·)表示所述近似模型。
对所公开的实施例的上述说明,使本领域专业技术人员能够实现或使用本发明。对这些实施例的多种修改对本领域的专业技术人员来说将是显而易见的,本文中所定义的一般原理可以在不脱离本发明的精神或范围的情况下,在其它实施例中实现。因此,本发明将不会被限制于本文所示的这些实施例,而是要符合与本文所公开的原理和新颖特点相一致的最宽的范围。
- 还没有人留言评论。精彩留言会获得点赞!