一种五自由度串联机器人的逆运动学通用求解方法与流程

本发明属于机器人逆运动学领域，具体涉及一种五自由度串联机器人的逆运动学通用求解方法。

背景技术：

机器人运动学是研究机器人末端姿态与各关节角度之间的关系，其中逆运动学是探讨在给定末端姿态的情况下，求解相对应的各关节角度值。逆运动学的求解精度直接影响机器人控制参数，即影响机器人最终的运动精度。对于串联机器人来说，逆解是不唯一的，它与机器人自身的结构有关。机器人逆解包括两大类：封闭解和数值解，其中数值解耗时、精度低；而封闭解则精度高、计算快，但其需要满足Pieper约束：三个相邻关节轴线交于一点或三个相邻关节轴线平行。目前大部分工业机器人采用末端三个关节轴线交于一点的结构，但即使在这样的约束条件下求逆解也是一件非常复杂的工作。Paden-Kahan等人提出一种将逆解问题化简成多个子问题进行求解的方法，该方法是基于POE(Product of Exponential)模型，相对D-H模型更加灵活、完备，这些子问题都是基于几何关系求解的，具有稳定的几何意义和数值稳定性，是近几年的研究热点。目前现有的子问题求解方法繁多，而且每一种子问题都有不同的求解方法，在应用的时候需要耗费时间去分析和计算，这为实际开发和应用带来很多不便。

技术实现要素：

针对现有技术中存在的上述技术问题，本发明提出了一种五自由度串联机器人的逆运动学通用求解方法，设计合理，克服了现有技术的不足，具有良好的效果。

为了实现上述目的，本发明采用如下技术方案：

一种五自由度串联机器人的逆运动学通用求解方法，包括如下步骤：

步骤1：求解机器人的肩部关节角度θ₁

根据指数积模型，机器人运动学方程可表示为：

且

其中，下标t和w分别表示末端工具坐标系与世界坐标系，θ是各关节的旋转角度向量θ＝[θ₁,...,θ₅]，g_wt(0)和g_wt(θ)分别表示在初始状态下和θ状态下末端工具坐标系相对世界坐标系的变换关系，为第i关节的运动旋量，包括关节轴的单位方向向量ω_i和轴上的任意一点r_i，ω_i和r_i被称为旋量参数，为第i关节坐标变换的指数表达形式，为是旋转矩阵的指数表达形式，其Rodrigues表达形式为：

空间任一向量p的齐次坐标用表示；

利用消元法消去机器人的腕部关节，设r₃是腕部关节的交点，将公式(1)两边同乘以可得：

其中根据旋量理论中的距离相等原则可知：

||c-r₂||＝||p-r₂|| (6)；

将带入公式(6)，两边平方后进行整理，并利用的Rodrigues旋转表达式将其化简为关于θ₁的三角函数公式：

x₁sinθ₁+y₁cosθ₁＝z₁ (11)；

其中为已知参数，则根据公式(11)可解得θ₁为：

其中

步骤2：求解机器人的肘部关节角度θ₂

将θ₁的值带入中可获得c的值，而c还可表示为：

将的Rodrigues表达式(3)带入式(15)，整理可得：

x₂sinθ₂+y₂cosθ₂＝z₂ (16)；

其中均已知，则根据公式(16)可解得θ₂的表达式为：

θ₂角度的具体象限由和的符号决定；

步骤3：求解机器人的腕部前两个关节角度θ₃和θ₄

将θ₁和θ₂带入公式(1)，并将已知项移到公式(1)的左边，可得：

将式(20)两边同乘以且r₅≠r₃，易知可得：

其中，可见公式(21)与公式(5)的形式相同，则根据θ₁和θ₂的表达式可给出θ₃和θ₄的表达式；

其中，且θ₄所在象限由和的符号来决定；

步骤4：求解机器人的腕部末端关节角度θ₅

将θ₁、θ₂、θ₃和θ₄带入公式(1)，并将已知项移到公式(1)的左边，可得：

将式(24)两边同乘以除r₅以外的点，这里取点p₂，可得：

其中，易得：

公式(26)与公式(15)形式相同，则可直接得出角度θ₅的表达式

其中，均已知，且θ₅所在象限由和的符号来决定。

本发明所带来的有益技术效果：

1、计算精度高，给出了各关节角度的封闭解，可利反三角函数直接求出，具有很高的计算精度；2、实现简单，每个关节的表达形式非常简单易懂，只需求解一次反三角函数即可；3、形式统一，5个关节可用两个表达式统一表达，容易记忆，方便应用。

附图说明

图1为5自由度机器人运动学简图。

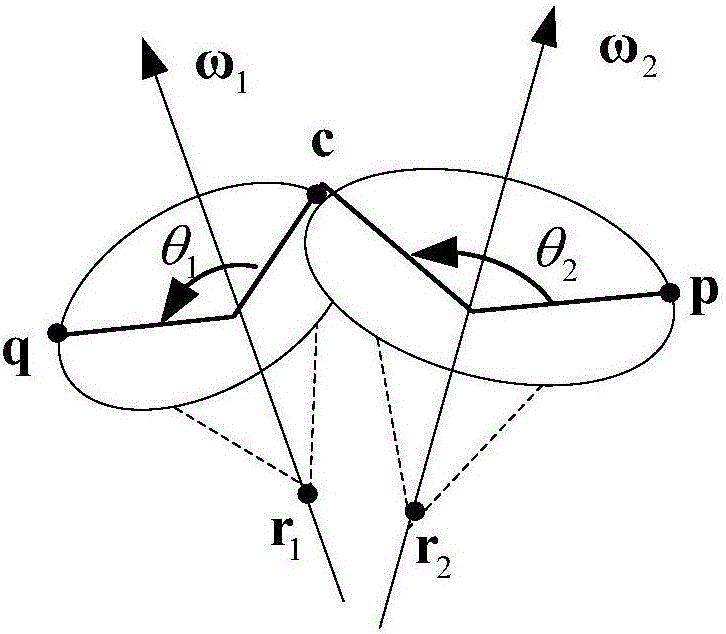
图2为两条任意轴线的结构简图。

其中，1-肩关节轴；2-肘关节轴；3-第一腕关节轴；4-第二腕关节轴；5-第三腕关节轴。

具体实施方式

下面结合附图以及具体实施方式对本发明作进一步详细说明：

如图1-2所示，针对5R机器人，包括肩关节轴1、肘关节轴2、第一腕关节轴3、第二腕关节轴4和第三腕关节轴5，腕部三条关节轴线相交于一点r₃，肩关节和肘关节的轴线相互异面。

根据指数积模型，机器人运动学方程可表示为：

且

其中，下标t和w分别表示末端工具坐标系与世界坐标系，θ是各关节的旋转角度向量θ＝[θ₁,...,θ₅]，g_wt(0)和g_wt(θ)分别表示在初始状态下和瞬时状态下末端工具坐标系相对世界坐标系的变换关系，为第i关节的运动旋量，包括关节轴的单位方向向量ω_i和轴上的任意一点r_i，ω_i和r_i被称为旋量参数，为第i关节坐标变换的指数表达形式，为是旋转矩阵的指数表达形式，其Rodrigues表达形式为：

为了叙述方便假设空间任一向量p的齐次坐标可用表示。

实施过程分为三步，第一步求解机器人的肩部和肘部关节角度，第二步求解机器人的腕部前两个关节角度，最后求解机器人腕部末端关节角。

1)求θ₁和θ₂。首先，针对图1所示机器人，利用消元法消去机器人的腕部关节，将五自由度的逆解问题转化为多个低自由度的子问题进行求解。设r₃是腕部关节的交点，将公式(3)两边同乘以r₃，可得：

根据旋量理论的位置保持不变原则可知：

则公式(4)变为：

其中根据旋量理论中的距离相等原则可知：

||c-r₂||＝||p-r₂|| (6)；

根据旋量理论的基本性质可知：

联立式(7)和式(8)相减，并将的表达式(2)带入，整理可得：

将公式(9)带入公式(6)可得：

将的Rodrigues表达式(3)带入式(10)，然后两边平方，整理可得：

x₁sinθ₁+y₁cosθ₁＝z₁ (11)；

其中：

设x₁＝ρcosφ，y₁＝ρsinφ，则利用三角函数的积化和差公式，公式(11)可变为：

其中同理可以得到：

则关节角度θ₁可表示为：

需要注意的是，在上式中需选择合适的r₁和r₂来保证需保证

将θ₁的值带入公式(9)中可获得c的值，而c还可表示为：

再将的Rodrigues表达式(3)带入上式，整理可得：

x₂sinθ₂+y₂cosθ₂＝z₂ (16)；

其中

由于则在公式(16)两边分别同乘以和可得：

则θ₂可表示为：

θ₂角度的具体象限由和的符号决定；

2)求θ₃和θ₄。将θ₁和θ₂带入公式(1)，并将已知项移到公式(1)的左边，可得：

将式(20)两边同乘以r₅，且r₅≠r₃，易知可得：

其中，可见公式(21)与公式(5)的形式相同，且r₃≠r₄≠r₀，r₀是两条轴线的交点，则根据θ₁和θ₂的表达式可给出θ₃和θ₄的表达式；

其中

其中，需要通过调整r₄来保证且θ₄所在象限根据和的符号来决定；

3)求θ₅。将θ₁、θ₂、θ₃和θ₄带入公式(1)，并将已知项移到公式(1)的左边，可得：

两边同乘以除r₅以外的点，这里取点p₂，可得：

其中根据公式(9)同理可得：

公式(26)与公式(15)形式相同，则可直接得出角度θ₅的表达式，

其中

θ₅所在象限由和的符号来决定。

当然，上述说明并非是对本发明的限制，本发明也并不仅限于上述举例，本技术领域的技术人员在本发明的实质范围内所做出的变化、改型、添加或替换，也应属于本发明的保护范围。