一种基于Z变换的脉冲成形中子伽马甄别方法与系统与流程

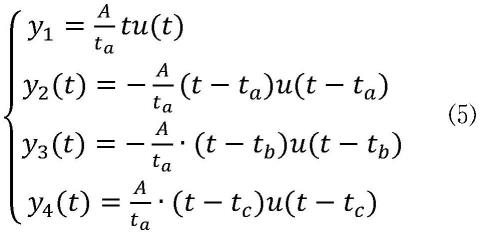
一种基于z变换的脉冲成形中子伽马甄别方法与系统
技术领域
1.本发明属于核辐射探测技术领域，具体涉及一种基于z变换的脉冲成形中子伽马甄别方法与系统。


背景技术：

2.随着世界核辐射探测技术领域的发展，中子的研究与应用得到了越来越多的科研工作者的关注，通常，核辐射包括了α辐射、β辐射、中子辐射和γ辐射等。对特定的辐射进行测量时，常伴随着其他类型的辐射，因此核脉冲波形甄别显得尤为重要。随着中子探测技术的不断发展，对中子的精准测量要求也越来越高。中子辐射场中往往伴随着γ粒子，这就需要对中子和γ粒子进行甄别。
3.现有技术中，中子、伽马甄别方法主要有电荷比较法、过零比较法、脉冲梯度法和上升时间法等。电荷比较法利用了中子和伽马射线产生的不同比例的快慢成分进行甄别。记总电荷量为q，慢电荷量为qs，通过计算qs/q进行甄别；脉冲梯度法的原理是利用中子与伽马下降部分的衰减差异进行甄别。选取脉冲峰值(t
p
,a
p
)处和距离峰值 25ns处的点(tc,ac)，计算脉冲的梯度进行甄别。脉冲梯度的计算方法为：
[0004][0005]
现有技术中存在以下技术问题：
[0006]
现有的甄别技术可以大致分为时域甄别方法、频域甄别方法和智能甄别方法。其中时域甄别法中的电荷比较法的慢电荷积分的开始时间和结束时间差对甄别效果影响较大，而脉冲梯度法利用的脉冲信息较少；而频域甄别方法中的小波变换法等实现过程复杂。
[0007]
在高计数率的adc采样下，获得的脉冲信号具有上升时间短，拖尾较长，而且现有的电荷比较法以及脉冲梯度法在对中子、伽马进行甄别时，涉及到了δt。在电荷比较法中，δt由慢电荷积分的开始时间和结束时间共同决定，在脉冲梯度法中，δt表示选取的两个采样点的时间差。δt无法正确选取影响到甄别效果的问题。


技术实现要素：

[0008]
针对上述现有技术中存在的问题，本发明提出了一种基于z变换的脉冲成形中子伽马甄别方法与系统，其目的为：利用梯形与反锯齿脉冲幅度之比进行甄别，既补偿了弹道亏损，也利用了较多的原始脉冲信息。通过与电荷比较法和脉冲梯度法对比，结果表明，该方法具有更好的甄别效果，既可以离线实现甄别，也可以通过成形系统实时甄别，且能够应用于复杂的测量环境。
[0009]
为实现上述目的本发明所采用的技术方案是：提供一种基于z变换的脉冲成形中子伽马甄别方法，包括：
[0010]
s1:获取探测器输出的原始信号，并对所述原始信号进行预处理，得到归一化并滤波的双指数信号；
[0011]
s2：进行预处理时观察脉冲的宽度，对一个脉冲设定时间阈值，然后判断所述脉冲在时间阈值内是否存在脉冲堆积；
[0012]
s3：基于s2的判断，将堆积脉冲舍弃掉，调节梯形成形和反锯齿成形的成形参数，对所述脉冲分别进行梯形成形和反锯齿成形，得到梯形成形信号和反锯齿成形信号；
[0013]
s4：提取s3所成形信号的信号幅度，然后通过统计梯形成形信号和反锯齿成形信号的幅度的比值进行中子、伽马的甄别。
[0014]
较优的，本发明s1中对原始信号进行预处理具体包括：
[0015]
s1.1：将原始信号取负获得正值信号；
[0016]
s1.2：取s1.1中的正值信号的任一段信号，且求取平均值作为基线，然后通过扣除该基线实现基线恢复；
[0017]
s1.3：对基线恢复后的信号进行滑动均值滤波；
[0018]
s1.4:对滑动均值滤波处理后的信号进行归一化处理，得到归一化并滤波的双指数信号。
[0019]
较优的，本发明s1.3具体为：定义yi为待平滑的第i道脉冲数据，将m个数据点做算术平均值作为该道的修正值，即：
[0020][0021]
较优的，本发明s2中，通过一阶导数法判断所述双指数信号在时间阈值内是否存在脉冲堆积，通过一阶导数法寻峰，当时间阈值内峰的个数大于1，则判定存在脉冲堆积，反之则不存在。
[0022]
较优的，本发明s3中，对所述双指数信号进行梯形成形具体为：
[0023]
s3.1：定义双指数信号如公式(2)所示：
[0024][0025]
其中，a为双指数信号的幅度，τ1和τ2均为时间常数；
[0026]
s3.2:对双指数信号离散化并进行z变换，得到双指数z变换信号，如公式(3) 所示：
[0027][0028]
其中，ts为adc的采样周期；
[0029]
s3.3：对双指数信号进行梯形成形，梯形在时域的表达式如公式(4)所示：
[0030][0031]
其中：
[0032][0033]
其中，ta为梯形的上升时间，tb为梯形的平顶时间，tc为梯形的脉冲宽度，且 tc＝ta+tb，a为脉冲幅度；
[0034]
令采样周期为ts时，对公式(4)进行z变换得：
[0035][0036]
其中，na＝ta/ts，nb＝tb/ts，nc＝tc/ts；
[0037]
从而得到梯形成形的传递函数：
[0038][0039]
将所述传递函数进行z逆变换，得到梯形成形的时域表达式：
[0040][0041]
较优的，本发明s3中，对所述双指数信号进行反锯齿成形具体为：
[0042]
s3.4:定义反锯齿信号的表达式如公式(9)所示：
[0043][0044]
其中：
[0045][0046]
式中，a为反锯齿的脉冲幅度；ta为反锯齿的脉冲宽度；u(t)为单位阶跃函数；
[0047]
令adc的采样周期为ts，t＝n
·
ts，ta＝na·
ts，将vo(t)离散化并且进行z变换，如下式所示：
[0048][0049]
从而得到反锯齿成形的传递函数hz为：
[0050]
[0051]
对式
⑿
进行z逆变换，推导出反锯齿成形的时域表达式：
[0052][0053]
其中：n＝t/ts，n是序列号；vi[n]是双指数输入序列，vo[n]是反锯齿输出序列。
[0054]
较优的，本发明s4中，将两种成形信号的幅度的比值定义为tips，即：
[0055][0056]
然后根据tips分布的散点图区分中子和伽马，对中子和伽马在不同tips下的计数进行统计，得到统计直方图，对统计得到的直方图进行高斯拟合，得到的中子和伽马的谱分布图，然后采用fom值作为评价指标，其表达式为：
[0057][0058]
其中，s为中子峰和伽马峰的间隔，γ
γ
为伽马峰的半高全宽，γn为中子峰的半高全宽。
[0059]
本发明还提出了一种基于z变换的脉冲成形中子伽马甄别系统，包括：
[0060]
预处理模块:获取探测器输出的原始信号，并对所述原始信号进行预处理，得到归一化并滤波的双指数信号；
[0061]
脉冲堆积判别模块：对原始信号进行预处理时观察脉冲的宽度，对一个脉冲设定时间阈值，判断所述双指数信号在时间阈值内是否存在脉冲堆积；
[0062]
脉冲成形模块：对所述双指数信号分别进行梯形成形和反锯齿成形，得到梯形成形信号和反锯齿成形信号；
[0063]
甄别模块：将堆积脉冲舍弃掉，然后通过脉冲成形模块得到梯形成形信号和反锯齿成形信号，提取这两种成形信号的幅度，然后通过统计这两种成形信号的幅度的比值进行中子、伽马的甄别。
[0064]
较优的，本发明脉冲成形模块中，对所述双指数信号进行梯形成形具体为：
[0065]
步骤1：定义双指数信号如公式(2)所示：
[0066][0067]
其中，a为双指数信号的幅度，τ1和τ2均为时间常数；
[0068]
步骤2:对双指数信号离散化并进行z变换，得到双指数z变换信号，如公式(3) 所示：
[0069]
[0070]
其中，ts为adc的采样周期；
[0071]
步骤3：对双指数信号进行梯形成形，梯形在时域的表达式如公式(4)所示：
[0072][0073]
其中：
[0074][0075]
其中，ta为梯形的上升时间，tb为梯形的平顶时间，tc为梯形的脉冲宽度，且 tc＝ta+tb，a为脉冲幅度；
[0076]
令采样周期为ts时，对公式(4)进行z变换得：
[0077][0078]
其中，na＝ta/ts，nb＝tb/ts，nc＝tc/ts；
[0079]
从而得到梯形成形的传递函数：
[0080][0081]
将所述传递函数进行z逆变换，得到梯形成形的时域表达式：
[0082][0083]
较优的，本发明脉冲成形模块中，对所述双指数信号进行反锯齿成形具体为：
[0084]
步骤4:定义反锯齿信号的表达式如公式(9)所示：
[0085][0086]
其中：
[0087][0088]
式中，a为反锯齿的脉冲幅度；ta为反锯齿的脉冲宽度；u(t)为单位阶跃函数；
[0089]
令adc的采样周期为ts，t＝n
·
ts，ta＝na·
ts，将vo(t)离散化并且进行z变换，如下式所示：
[0090][0091]
从而得到反锯齿成形的传递函数hz为：
[0092][0093]
对式
⑿
进行z逆变换，推导出反锯齿成形的时域表达式：
[0094][0095]
其中：n＝t/ts，n是序列号；vi[n]是双指数输入序列，vo[n]是反锯齿输出序列。
[0096]
相比现有技术，本发明的技术方案具有如下优点/有益效果：
[0097]
1.本发明采用了脉冲成形方法，相比于其他的甄别方法，能够降低噪声的影响，补偿弹道亏损，还可以利用更多的脉冲信息，并且可以满足不同的采样率，既可以离线甄别，也可以实时甄别，实现简单。
[0098]
2.本发明将采集得到的双指数信号进行梯形成形和反锯齿成形，利用梯形与反锯齿脉冲幅度之比进行甄别，既抵消了弹道亏损的影响，也利用了较多的原始脉冲信息。通过与电荷比较法和脉冲梯度法对比，具有更好的甄别效果，既可以离线实现甄别，也可以通过成形系统实时甄别，能够用于复杂的测量环境。
[0099]
3.本发明构建了快慢双通道的脉冲成形算法。在慢通道，对脉冲进行脉冲宽度可调节的梯形成形，可以补偿弹道亏损，减小拖尾，并且容易提取脉冲幅度。在快通道，对脉冲进行反锯齿成形，该形状具有较短的成形时间，实现较低的信号丢失率。由于不同的粒子在快慢通道成形后的脉冲幅度比值不同，可以利用两者幅度之比进行脉冲形状甄别。
附图说明
[0100]
为了更清楚地说明本发明实施方式的技术方案，下面将对实施方式中所需要使用的附图作简单地介绍，应当理解，以下附图仅示出了本发明的某些实施例，因此不应被看作是对范围的限定，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他相关的附图。
[0101]
图1是本发明原始信号示意图。
[0102]
图2是图1的原始信号取负值示意图。
[0103]
图3是图2的脉冲信号基线恢复示意图。
[0104]
图4是图3经过均值滑动滤波后信号示意图。
[0105]
图5是图4经过归一化处理后信号示意图。
[0106]
图6是梯形成形信号示意图。
[0107]
图7是反锯齿成形信号示意图。
[0108]
图8是反锯齿成形信号基线恢复示意图。
[0109]
图9是tips分布的散点图。
[0110]
图10是中子和伽马的谱分布图。
[0111]
图11是中子和伽马甄别的fom图。
[0112]
图12是梯形脉冲示意图。
[0113]
图13是反锯齿脉冲示意图。
具体实施方式
[0114]
为使本发明目的、技术方案和优点更加清楚，下面对本发明实施方式中的技术方案进行清楚、完整地描述，显然，所描述的实施方式是本发明的一部分实施方式，而不是全部的实施方式。基于本发明中的实施方式，本领域普通技术人员在没有作出创造性劳动前提下所获得的所有其他实施方式，都属于本发明保护的范围。因此，以下提供的本发明的实施方式的详细描述并非旨在限制要求保护的本发明的范围，而是仅仅表示本发明的选定实施方式。
[0115]
实施例1：
[0116]
在利用闪烁体探测器测量射线时，中子和伽马射入灵敏体积时会产生大量的次级粒子，由于中子与伽马的质量阻止本领不同，导致在灵敏体积内的能量沉积也不同，从而获得电压信号在波形上有差异。而且，经研究表明，中子与伽马在与闪烁体发生反应时，产生的闪烁光脉冲中的快慢成分占比是不同的。中子脉冲快成分占比小，慢成分占比大，伽马射线与之相反。因此，本实施例1基于该原理，提出了一种基于z 变换的脉冲成形中子伽马甄别方法，包括：
[0117]
s1:获取探测器输出的原始信号，如图1所示，并对所述原始信号进行预处理，得到归一化并滤波的双指数信号；s1中对原始信号进行预处理具体包括：
[0118]
s1.1：将原始信号取负获得正值信号，如图2所示；
[0119]
s1.2：取s1.1中的前110个信号，且求取平均值作为基线，然后通过扣除该基线实现基线恢复，如图3所示；
[0120]
s1.3：对基线恢复后的信号进行滑动均值滤波，具体为：
[0121]
定义yi为待平滑的第i道脉冲数据，将m个数据点做算术平均值作为该道的修正值，即：
[0122][0123]
在本实施例1中，m取10。滑动均值滤波后的信号波形如图4所示。
[0124]
s1.4:对滑动均值滤波处理后的信号进行归一化处理，得到归一化并滤波的双指数信号，本实施例1将数据映射到(0，1)上，如图5所示。
[0125]
在高计数率的情况下，往往会出现脉冲堆积的现象，这会造成脉冲幅度难以提取，能量分辨率不高，所以脉冲堆积的判别尤为重要。
[0126]
s2：通过预处理时观察脉冲的宽度，对一个脉冲设定时间阈值，本实施例的时间阈值为402ns，在没有脉冲堆积的情况下，402ns内只有一个峰；通过一阶导数法判断所述双指数信号在时间阈值内是否存在脉冲堆积，通过一阶导数法寻峰，当时间阈值内峰的个数大
于1，则判定存在脉冲堆积，反之则不存在。对脉冲信号求一阶导数，一阶导数由正变为负，过零点所对应的道值即为峰位，一阶导数由负变为正，过零点所对应的道值为峰边界。
[0127]
s3：对所述双指数信号将堆积脉冲舍弃之后，分别进行梯形成形和反锯齿成形，得到梯形成形信号和反锯齿成形信号，如图6和图7所示；具体为：
[0128]
s3.1：定义双指数信号如公式(2)所示：
[0129][0130]
其中，a为双指数信号的幅度，τ1和τ2均为时间常数；
[0131]
s3.2:对双指数信号离散化并进行z变换，得到双指数z变换信号，如公式(3) 所示：
[0132][0133]
其中，ts为adc的采样周期；
[0134]
s3.3：对双指数信号进行梯形成形，梯形脉冲示意图如图12所示，梯形在时域的表达式如公式(4)所示：
[0135][0136]
其中：
[0137][0138]
其中，ta为梯形的上升时间，tb为梯形的平顶时间，tc为梯形的脉冲宽度，且 tc＝ta+tb，a为脉冲幅度；
[0139]
令采样周期为ts时，对公式(4)进行z变换得：
[0140][0141]
其中，na＝ta/ts，nb＝tb/ts，nc＝tc/ts；
[0142]
从而得到梯形成形的传递函数：
[0143][0144]
将所述传递函数进行z逆变换，得到梯形成形的时域表达式：
[0145][0146]
s3.4:反锯齿脉冲示意图如图13所示，定义反锯齿信号的表达式如公式(9)所示：
[0147][0148]
其中：
[0149][0150]
式中，a为反锯齿的脉冲幅度；ta为反锯齿的脉冲宽度；u(t)为单位阶跃函数；
[0151]
令adc的采样周期为ts，t＝n
·
ts，ta＝na·
ts，将vo(t)离散化并且进行z变换，如下式所示：
[0152][0153]
从而得到反锯齿成形的传递函数hz为：
[0154][0155]
对式
⑿
进行z逆变换，推导出反锯齿成形的时域表达式：
[0156][0157]
其中：n＝t/ts，n是序列号；vi[n]是双指数输入序列，vo[n]是反锯齿输出序列。
[0158]
由反锯齿成形结果可知，反锯齿有较强的基线漂移，这与成形算法的收敛性有关。为了抑制基线漂移，将输入信号的第一列之前增加一列0，之后进行反锯齿成形。修正后的反锯齿成形如图9所示，可见成形后的脉冲基线得到恢复。
[0159]
s4：通过s3得到梯形成形信号和反锯齿成形信号，提取这两种成形信号的幅度，然后通过统计这两种成形信号的幅度的比值进行中子、伽马的甄别；
[0160]
将两种成形信号的幅度的比值定义为tips，即：
[0161]
[0162]
计算得到的tips分布的散点图如图9所示，比值较大的为中子，比值较小的为伽马，可见采用梯形幅度与反锯齿幅度之比的方法可以甄别中子和伽马。
[0163]
然后根据tips分布的散点图区分中子和伽马，对中子和伽马在不同tips下的计数进行统计，得到统计直方图，对统计得到的直方图进行高斯拟合，得到的中子和伽马的谱分布图，如图10所示，然后采用fom值作为评价指标，其表达式为：
[0164][0165]
其中，s为中子峰和伽马峰的间隔，γ
γ
为伽马峰的半高全宽，γn为中子峰的半高全宽，各参数图示如图11所示。
[0166]
在实际测量中，受到电路噪声的影响，脉冲有较快的上升沿和较长的拖尾，而且高速采样率会造成脉冲堆积，由于实验中堆积脉冲个数较少，所以直接舍弃堆积脉冲。
[0167]
本实施例1通过公式(15)计算图10的fom值，得到fom＝4.0391，为了验证该方法具有甄别效果好的优势，与传统的时域下的电荷比较法和脉冲梯度法进行了比较：
[0168]
电荷比较法利用了中子和伽马射线产生的不同比例的快慢成分进行甄别。记总电荷量为q，慢电荷量为qs，通过计算qs/q进行甄别，得到的fom值为2.2064。
[0169]
脉冲梯度法的原理是利用中子与伽马下降部分的衰减差异进行甄别。选取脉冲峰值(t
p
,a
p
)处和距离峰值25ns处的点(tc,ac)，计算脉冲的梯度进行甄别。脉冲梯度的计算方法为：
[0170]
通过计算得到的fom值为3.0618。
[0171]
下表表示了三种方法的甄别效果。
[0172]
表3不同方法的甄别效果对比
[0173][0174]
由上表可知，本文提出的脉冲成形的方法相较于电荷比较法和脉冲梯度法，有较好的甄别效果。
[0175]
本实施例1还提出了一种基于z变换的脉冲成形中子伽马甄别系统，包括：
[0176]
预处理模块:获取探测器输出的原始信号，对其进行归一化预处理，生成双指数信号；
[0177]
脉冲堆积判别模块：对原始信号进行预处理时观察脉冲的宽度，对一个脉冲设定时间阈值，判断所述双指数信号在时间阈值内是否存在脉冲堆积；
[0178]
脉冲成形模块：对所述双指数信号分别进行梯形成形和反锯齿成形，得到梯形成形信号和反锯齿成形信号；具体为：
[0179]
步骤1：定义双指数信号如公式(2)所示：
[0180][0181]
其中，a为双指数信号的幅度，τ1和τ2均为时间常数；
[0182]
步骤2:对双指数信号离散化并进行z变换，得到双指数z变换信号，如公式(3) 所示：
[0183][0184]
其中，ts为adc的采样周期；
[0185]
步骤3：对双指数信号进行梯形成形，梯形在时域的表达式如公式(4)所示：
[0186][0187]
其中：
[0188][0189]
其中，ta为梯形的上升时间，tb为梯形的平顶时间，tc为梯形的脉冲宽度，且 tc＝ta+tb，a为脉冲幅度；
[0190]
令采样周期为ts时，对公式(4)进行z变换得：
[0191][0192]
其中，na＝ta/ts，nb＝tb/ts，nc＝tc/ts；
[0193]
从而得到梯形成形的传递函数：
[0194][0195]
将所述传递函数进行z逆变换，得到梯形成形的时域表达式：
[0196][0197]
步骤4:定义反锯齿信号的表达式如公式(9)所示：
[0198][0199]
其中：
[0200][0201]
式中，a为反锯齿的脉冲幅度；ta为反锯齿的脉冲宽度；u(t)为单位阶跃函数；
[0202]
令adc的采样周期为ts，t＝n
·
ts，ta＝na·
ts，将vo(t)离散化并且进行z变换，如下式所示：
[0203][0204]
从而得到反锯齿成形的传递函数hz为：
[0205][0206]
对式
⑿
进行z逆变换，推导出反锯齿成形的时域表达式：
[0207][0208][0209]
其中：n＝t/ts，n是序列号；vi[n]是双指数输入序列，vo[n]是反锯齿输出序列。
[0210]
甄别模块：将堆积脉冲舍弃掉，然后通过脉冲成形模块得到梯形成形信号和反锯齿成形信号，提取这两种成形信号的幅度，然后通过统计这两种成形信号的幅度的比值进行中子、伽马的甄别；
[0211]
以上仅是本发明的优选实施方式，应当指出的是，上述优选实施方式不应视为对本发明的限制，本发明的保护范围应当以权利要求所限定的范围为准。对于本技术领域的普通技术人员来说，在不脱离本发明的精神和范围内，还可以做出若干改进和润饰，这些改进和润饰也应视为本发明的保护范围。