一种坐标变换并行计算方法和装置与流程

本发明涉及数字处理技术领域，尤其涉及基于cordic算法的三角函数计算与矢量变换的并行计算。

背景技术：

坐标旋转数字计算机cordic(coordinaterotationdigitalcomputer，简称cordic)由j.volder于1959年提出的，它是一种用于计算常用超越函数的循环迭代算法，其基本思想是是通过一系列的只与运算基数有关的固定小角度的不断偏摆来逼近所要旋转的角度。为了扩展可计算函数的个数，1971年j.wahher提出了统一cordic算法，即把圆周坐标、线性坐标和双曲坐标统一到同一个cordic迭代方程中。

cordic算法因为能够将多种难以用硬件电路直接实现的复杂运算分解为简单的加减法和移位操作，所以很适合用数字电路来实现，因而其应用范围也就极其广泛，比如数控振荡器、正余弦函数发生器、数字频率合成器等。

下面介绍旋转模式圆周坐标下的cordic算法：

在平面坐标系下，将向量(x1，y1)旋转到如附图1的向量(x2，y2)，两个向量之间满足如式1所示的运算关系。

对所旋转θ角度进行分解，将其分成n个递减的小旋转角θi，即其中θi，δi为判决算子，用于确定旋转的方向。当顺时针旋转θi角度时，δi为-1；当逆时针旋转θi角度时，δi为1.每次小的角度旋转都有

再令θi＝tan^-12^-i，即tanθi＝2^-i。

这样，平面坐标系中的向量(x1，y1)经过n次圆周旋转之后达到同一坐标平面中的向量(x2，y2)，该旋转过程可表示为

其中k为伸缩因子

其中，k值可以提前计算出，k＝0.607529350088。

此时若令x1＝k，y1＝0，可得出x2＝cosθ，y2＝sinθ。

通过上述的理论推导，平面向量(x1，y1)的旋转计算问题就可以由如下基本计算式迭代n次实现。此时第i次的迭代公式就转变为下式：

由上式可知道，传统的cordic算法中，每一步的旋转方向都要根据上一步的结果进行判断，即δi＝sign(zi)。要想得到n位的精度，需要至少迭代n次，需要n个时钟周期才能完成一次计算。为了提高运算速度，最有效的办法就是减少z通路的计算，提高运算的并行度。

tso-bingjuang，shen-fuhsiao等人于2004年提出并行cordic算法。其思想是根据输入角度的n位二进制表示，将其分为高m位和低n-m位，先对高位实施binary-to-bipolar(bbr)转换，一次产生高位的旋转次序，然后将高位产生的角度误差叠加在低位，然后在对低位采用bbr转换，一次产生低位的旋转次序。为了维持统一的矫正因子k，对于一次高位旋转2^-i的弧度，采用若干次统一方向的微旋转进行补偿(此方法称为microrotationanglerecoding)，使其在第i次旋转产生的误差可以在低位进行补偿而不会产生高位的精度损失。该方法的虽然实现了cordic的并行处理，但增加了很多补偿的微旋转(在输入角度位数为32位时，需要额外8次微旋转)，造成x/y路径的延迟加大。公布号为cn102073471a，已授权生效的发明专利“一种处理器cordic迭代运算方法及电路”将三次迭代运算并行展开，目的是想一次计算三次迭代，但是这三次迭代的方向无法在开始迭代前确定，还是需要在计算通路中确定，实际上并没有使运算加速多少。目前大部分cordic算法都是采用流水线计算或者迭代结构。得到一个计算的值往往需要很多时钟周期，非常不利于cordic算法在fpga上的快速实现。

技术实现要素：

针对现有技术的缺点，提出一种新型的低z通路判断，低延迟，高精度的并行cordic计算方法和装置。

旋转弧度可用二进制表示为其中i∈{0,1}，θ≤π/4。

将输入的弧度拆分成三个部分：高位，中位，低位：

m是满足2^-m-tan^-12^-m<2^-n的最小值，可得出m＝[(n-log23)/3]。当i≥m时，tan2^-i＝2^-i。l为n/2，此时模矫正因子

根据现有技术对θ^h进行bbr转换，可得到：

根据(9)式，因为bi-1∈{0,1}，所以ri∈{-1,1}，由此可根据输入弧度的高m-1位直接得到1到m次旋转方向及r1,r2,…,rm的值。

此时，理想的情况下1到m次的旋转的角度都为2^-i，i＝1,2,…,m。但此时i＝1,2,…,m-1.硬件上难以实现tan2^-i。

对弧度2^-i进行量化处理可由下式表示：

为第i次旋转的角度值。如图2所示，实线为第i次旋转目标角度，虚线为实际旋转角度，若旋转超过目标角度，角度误差-εi，若旋转未达到目标角度，角度误差为εi。

此时第i次变换矩阵变为：

σj的取值满足式12的前提下，取

1到m-1次旋转由式(11)替代，由式(10)可得θ^h产生的剩余角度为：

结合式(12)和式(16)可知所以σj满足式(12)就可以将高位产生的误差传递到低位而不会丢失精度。变换矩阵(11)硬件上可由简单的移位和相加实现。

进一步的经过前m次转换，剩余弧度为:

对θ^m′继续采用与θ^h同样的转换，得到:

其中rm＝1-2b′m-1,ri＝(2bi-1-1)，i＝m+1，m+2,…，l.

根据式(18)可得rm,rm+1,…,rl次旋转的值，因为i在这个区间内，满足tan^-12^-i＝2^-i，转换矩阵变为传统矩阵如下：

经过第二阶段l-m次旋转，剩余弧度为:

在i∈[l,n]，由于模矫正因子cosθi＝1，可以得出若后续的某些旋转没有进行，也能保持统一的模校正因子，所以无需进行变换，此时可根据θ^l″进行简单的单向旋转，对于bi″＝0的不进行旋转，bi″＝1的进行单向旋转。直接根据二进制所在位的值，直接确定剩余旋转的次序。更进一步的，当i>n/2，任意的两次相邻的旋转由下式表示：

式(21)中2^-(m+n)<2^-n，已超出了最小精度，所以式(21)可简化为：

由式(22)可得n/2到n次旋转可压缩成下面矩阵表示：

式(23)中，若剩余弧度为负，则s为-1，否则为1。式(23)可由两次无符号乘法，两次加法实现。

上述中旋转方向的预测可分为两步，第一步根据θ^h得出r1,r2,…,rm的值，第二步根据θ^m′+θ^l′，对θ^m′和θ^l′采用不同的预测方法，可同时得出rm,rm+1,…,rl,rl,…,rn的值。所以整体的并行cordic运算只要两拍。

根据上述推导，伪旋转产生的总校正因子可以提前计算出来，不会因为输入角度不同而不同，保留了传统cordic算法的优点，且不需要额外的微旋转进行补偿。

附图说明：

图1是cordic算法旋转示意图。

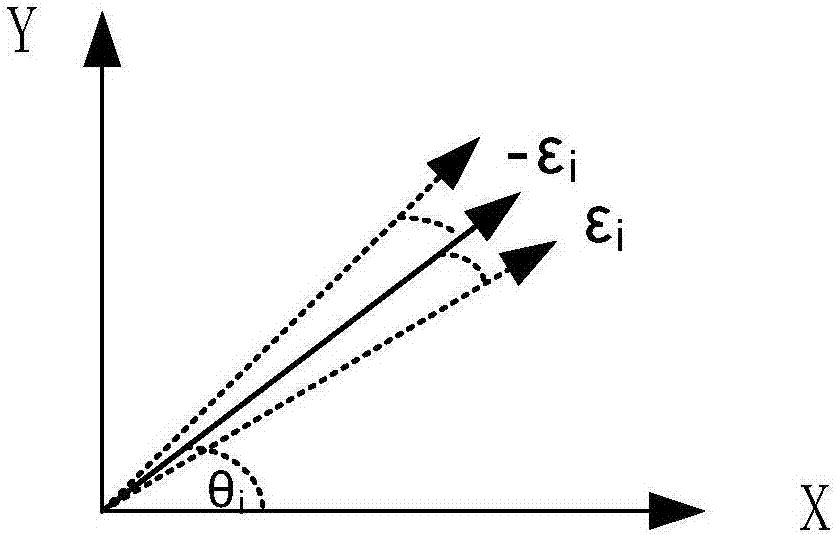
图2是第i次旋转误差产生示意图。

图3是式(11)的旋转矩阵结构示意图。

图4是本实施例32位系统第一旋转矩阵硬件结构示意图。

图5是本实施例总体结构示意图。

具体实施方式：

本发明的具体实施步骤为：

(1)对输入的xin，yin，zin进行变换，使输入角度值调整到(0，π/4)区间内。对调整后的弧度拆分成三个部分：高位，中位，低位：

(2)对θ的前m-1次进行预测得出r1,r2,…,rm的值，对前m-1旋转的目标角度进行量化，产生新的旋转矩阵。将前m次旋转误差累计到低位，得到新的θ^m′+θ^l′，根据θ^m′+θ^l′，对θ^m′和θ^l′采用不同的预测方法，可同时得出rm,rm+1,…,rl,rl,…,rn的值。

(3)对m到l次旋转采用传统矩阵，对l到n次旋转利用乘法直接求得。最后进行象限恢复输出计算得到的三角函数值。

本实施例以32位的系统为例进行说明，对于一个32位系统，最大的弧度为2π，所以采用3位二进制表示整数和29位二进制表示小数。对于输入弧度不在(0，π/4)区间中的，根据现有的区间折叠技术，很容易将输入的弧度调整到(0，π/4)中，这里不在赘述。

调整后的弧度可表示为其中bi∈{0,1}，θ≤π/4。

将输入的弧度拆分成三个部分：高位，中位，低位：

对于θ^h进行bbr转换，得到：

根据式(27)可一次得到r1,r2,…,r10的值。

前10次的微旋转角度和矩阵为：

θ1＝tan^-1(2^-1+2^-5+2^-6)(28)

θ2＝tan^-1(2^-2+2^-8+2^-10)(30)

θ3＝tan^-1(2^-3+2^-11+2^-13)(32)

θ4＝tan^-12^-4(34)

θ5＝tan^-12^-5(35)

θ6＝tan^-12^-6(37)

θ7＝tan^-12^-7(38)

θ8＝tan^-12^-8(39)

θ9＝tan^-12^-9(40)

θ10＝tan^-12^-10＝2^-10(41)

4到10次采用传统的旋转矩阵

由上述各个微旋转产生的误差为：

ε1＝|2^-1-θ1|＝0.00044＝o(2^-12)(42)

ε2＝|2^-2-θ2|＝0.00043＝o(2^-12)(43)

ε3＝|2^-3-θ3|＝0.00008＝o(2^-14)(44)

ε4＝|2^-4-θ4|＝0.000081＝o(2^-14)(45)

ε5＝|2^-5-θ5|＝0.00001＝o(2^-17)(46)

ε6＝|2^-6-θ6|＝0.000001＝o(2^-20)(47)

ε7＝|2^-7-θ7|＝o(2^-23)(48)

ε8＝|2^-8-θ8|<o(2^-23)(49)

ε9＝|2^-9-θ9|<o(2^-23)(50)

由θ^h产生的误差最大弧度为

预先将每一个微旋转的误差值制表保存。每一步旋转的误差值用保留进位加法器叠加产生新的

对中位θ^m′进行数学转换可得到

r10＝1-2b′9,ri＝(2bi-1-1)，i＝11,12,…,15(51)

可直接得到r10,r11,r12,r13,r14,r15的值。对i∈[10,15]采用传统的旋转矩阵。

后15到29次旋转矩阵可由下式表示：

根据式的原码表示，若为负，s＝-1，反之，s＝1。ri与位权2^-i所在位的值相等，ri∈{0,1}。15到29次旋转直接由两次乘法，两次加法实现。上述中旋转方向的预测可分为两步，第一步根据θ^h得出r1,r2,…,r9的值，第二步根据θ^m′+θ^l′，对θ^m′和θ^l′采用不同的预测方法，可同时得出r10,…,r15,r15,…,r29的值。

下面结合附图5进行说明：

附图5中1为前处理模块，采用区间折叠技术，对输入的xin，yin，zin进行变换，使输入角度值调整到(0，π/4)区间内，并输出象限信息。

附图5中3为第一角度预测模块，对调整后的弧度拆分成三个部分：高位，中位，低位：

对θ^h进行数学转换，重编码后一次产生r1,r2,…,r10。各个值的确定方法如下：由于调整后的弧度一直为正，所以r1＝1，ri＝1-2bi-1。确定r1,r2,…,r10值后，结合α1,α2,…,α9的值，每次旋转后产生的角度误差与θ^m+θ^l相加形成θ^m′+θ^l′。

上面提到的α1,α2,…,α9由每次旋转后的误差值确定，若实际转过的角度大于目标角度，则当前次αi＝-1，若实际转过的角度小于目标角度，则当前次αi＝1。

附图5中2为第一旋转模块包含10次旋转。第一级旋转的角度为θ1＝tan^-1(2^-1+2^-5+2^-6)，转换矩阵为：第二级旋转的角度为θ2＝tan^-1(2^-2+2^-8+2^-10)，转换矩阵为第三级旋转的角度为θ3＝tan^-1(2^-3+2^-11+2^-13)，转换矩阵为后面四级到十级旋转角度依次为θ4＝tan^-12^-4，θ5＝tan^-12^-5，θ6＝tan^-12^-6，θ7＝tan^-12^-7，θ8＝tan^-12^-8，θ9＝tan^-12^-9，θ10＝tan^-12^-10＝2^-10，转换矩阵为传统的矩阵。r1,r2,…,r10由第一角度预测模块得到后，开始由第一级到第十级依次计算，x/y通路的延迟严格保持一样。在x/y加法的计算中，根据现有技术，可选择csa加法器合成的4-2压缩加法器加速计算，计算完的x/y值输入第二选择模块。

附图5中5为第二角度预测模块，第一角度预测模块累加的剩余角度传入第二角度预测模块。对剩余角度的第10到第14位进行与第一预测模块高位值相同的等式变换，产生r10,r11,r12,r13,r14,r15的值，同时产生低n/2位的剩余角度θ^l″，根据θ^l″的值产生r15,…,r29的值。r10＝1-2b′9,r11＝2b′10-1,r12＝2b′11-1,r13＝2b′12-1,r14＝2b′13-1,r15＝2b′14-1。r15,…,r29与θ^l″的原码对应，r15＝b″15,…,，r29＝b″29。

附图5中4为第二旋转计算模块包括6次传统旋转计算和一次乘法计算。第二旋转模块接收第一旋转模块的x/y的输出，接收第二角度预测模块输出的r9,r10,…,r15,r15,…,r29的值。r9,r10,…,r15用于确定第10级到第15级传统旋转的方向。r15,…,r29的值确定15位的乘数。

附图5中6为后处理模块，后处理模块对第二旋转计算模块的x/y根据1中输出的象限信息进行象限的恢复。最后输出x/y的值。