一种强鲁棒性1比特压缩贝叶斯感知方法与流程

本发明属于信号检测与估计(signal detection and estimation)技术领域，特别涉及一种利用变形最大期望(variational expectation-maximization，V-EM)算法同时识别符号反转误差和估计稀疏信号的鲁棒贝叶斯压缩感知方法。

背景技术：

传统的1比特压缩感知算法都认为1比特测量是无误的，但由于信号采集与传输的过程中都会引入噪声，因此有些比特可以已经反转到了与之前相反的状态，这会导致这些传统算法有相当大的性能损失。

目前已经有一些算法考虑到了符号反转问题，如自适应异常值追踪算法、自适应噪声归一化固定点迭代算法等，这些算法可以自动找到符号反转误差。但这些算法都需要知道反转误差的数目，这是不可能提前获知的，因此这些算法的实用性并不高。本发明中，通过将符号反转误差建模成一个稀疏噪声向量的扰动未量化的观测值，从而利用贝叶斯理论来精确确定反转误差和稀疏信号。

技术实现要素：

本发明的目的在于提供一种强鲁棒性1比特压缩贝叶斯感知方法。本发明通过将符号反转误差建模成一个稀疏噪声向量的扰动未量化的观测值，并在该稀疏噪声向量上施加逆高斯-Gamma分层先验来促进稀疏，通过使用贝叶斯理论，即可完成对符号反转误差和稀疏信号的联合估计。通过联合估计即可精确确定符号反转误差的数目与位置。

为了方便描述，首先对本发明使用系统模型和术语进行介绍：

设1比特量化问题中，t＝sign(y)＝sign(Ax+w)，其中，为二进制观测值，为未量化的原始测量值，为一个稀疏噪声向量，即仅有很少的非零系数，sign表示对向量元素取符号函数，若该元素大于0，返回1，否则返回0。

K-稀疏信号为随机产生的，K-稀疏信号的支撑集是根据一个均匀分布随机选取的。测量矩阵中的每个值都是从一个零均值单位方差的高斯分布中随机产生的，并且它的每一列都进行了归一化。符号反转误差也是根据一个均匀分布随机产生的，其中，m＝200,n＝100,K＝10,L＝10。

感知矩阵：用以对信号进行线性采样，起到降维的作用，把n维信号映射到m维空间，通常m<<n。

稀疏性：信号可以用一组基或者一个字典中若干元素线性表示。当这种表示是精确的，就称这个信号是稀疏的。大多数的高维信号所包含的信息远远低于它的维度所能包含的，稀疏信号模型为这种高维信号提供了数学上的解释。

稀疏表示：信号可以用一组基中若干元素线性表示，就称这组基为稀疏基。稀疏的信号在稀疏基下的表示即为信号的稀疏表示。

一种强鲁棒性1比特压缩贝叶斯感知方法，具体步骤如下：

S1、构造具有随机采样性质的感知矩阵A，对信号进行采样得到y，设置误差预设值ε；

S2、构造各个参数的先验、后验分布：

t关于y的后验分布为：其中，σ(y_i)＝1/(1+exp(-y))为逻辑函数，且为可导的，

x、w的高斯逆Gamma先验为：

S3、构建目标函数，具体为：

S31、引入之间变量δ，根据Jaakkola-Jordon不等式

其中，z＝(2t-1)y，

λ(δ)＝(1/4δ)tanh(δ/2)，tanh(δ)＝(exp(x)-exp(-x))/(exp(x)+exp(-x))；

S32、构建替代函数

S33、令θ＝{x,α,w,β}，构建目标函数G(t,θ,δ)＝F(t,x,w,δ)p(x|α)p(α)p(w|β)p(β)；

S4、令q(θ)＝q_x(x)q_α(α)q_w(w)q_β(β)，利用V-EM算法更新各参数：

S41、更新q_x(x)：

其中，Λ_α＝diag(α₁,...α_n)，

Λ_δ＝diag(λ(δ₁),...λ(δ_m))，则x的均值方差分别为Φ_x＝(Λ_<α>+2A^TΛ_δA)^-1，Λ_<α>＝diag(<α₁>,…<α_n>)，<α_i>为α_i关于分布q_α(α)的期望；

S42、更新q_w(w)：

其中，Λ_<β>＝diag(<β₁>,...<β_n>)，<β_i>为β_i关于分布q_β(β)的期望，因此w的均值方差分别为Φ_w＝(Λ_<β>+2Λ_δ)^-1；

S43、更新q_α(α)：

其中，为关于分布q_x(x)的期望，因此α服从如下Gamma分布：其中，则α_i的期望为

S44、更新q_β(β)：

其中，为关于分布q_w(w)的期望，因此β服从如下Gamma分布：其中则α_i的期望为

S45、对求导，可得令上式为0可得

其中，<xx^T>＝μ_xμ_x^T+Φ_x；

S6、如果上述迭代过程满足终止条件停止迭代，否则返回S4进行下一次迭代。

本发明的有益效果是：

本发明不需要知道符号反转数的先验信息和稀疏信号的稀疏程度，同时也不需要其他的设计参数，在比特反转误差数目较多的情况下，本发明相比其他算法有更大的性能优势。

附图说明

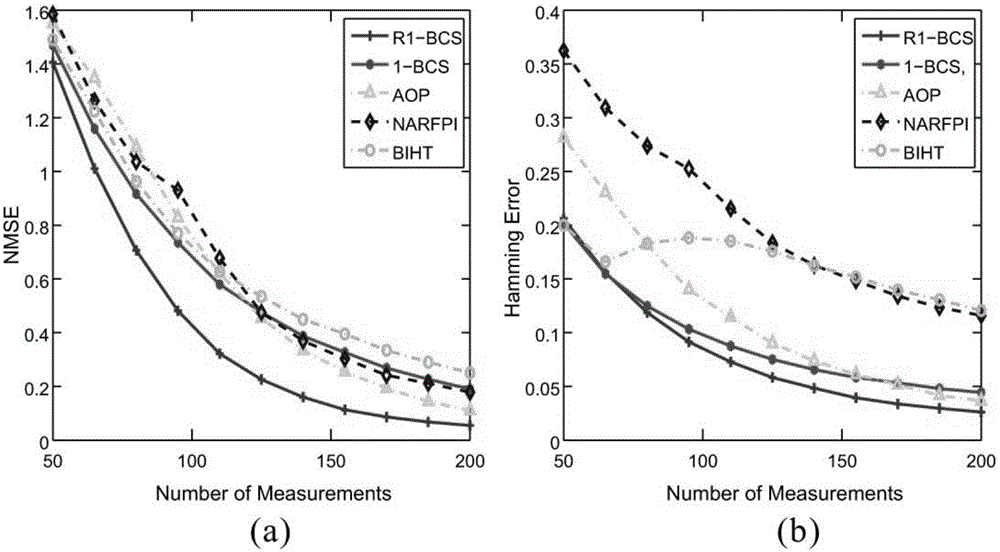
图1为各算法比特反转误差数目L与NMSE、汉明误差的关系。

图2为各算法测量次数m与NMSE、汉明误差的关系。

具体实施方式

下面结合具体实施例，对本发明作进一步地详细描述。

S1、构造具有随机采样性质的感知矩阵A，对信号进行采样得到y，设置误差预设值ε；

S2、构造各个参数的先验、后验分布：

t关于y的后验分布为：其中，σ(y_i)＝1/(1+exp(-y))为逻辑函数，且为可导的，

x、w的高斯逆Gamma先验为：

S3、构建目标函数，具体为：

S31、引入之间变量δ，根据Jaakkola-Jordon不等式

其中，z＝(2t-1)y，

λ(δ)＝(1/4δ)tanh(δ/2)，tanh(δ)＝(exp(x)-exp(-x))/(exp(x)+exp(-x))；

S32、构建替代函数

S33、令θ＝{x,α,w,β}，构建目标函数G(t,θ,δ)＝F(t,x,w,δ)p(x|α)p(α)p(w|β)p(β)；

S4、令q(θ)＝q_x(x)q_α(α)q_w(w)q_β(β)，利用V-EM算法更新各参数：

S41、更新q_x(x)：

其中，Λ_α＝diag(α₁,...α_n)，

Λ_δ＝diag(λ(δ₁),...λ(δ_m))，则x的均值方差分别为Φ_x＝(Λ_<α>+2A^TΛ_δA)^-1，Λ_<α>＝diag(<α₁>,...<α_n>)，<α_i>为α_i关于分布q_α(α)的期望；

S42、更新q_w(w)：

其中，Λ_<β>＝diag(<β₁>,...<β_n>)，<β_i>为β_i关于分布q_β(β)的期望，因此w的均值方差分别为Φ_w＝(Λ_<β>+2Λ_δ)^-1；

S43、更新q_α(α)：

其中，为关于分布q_x(x)的期望，因此α服从如下Gamma分布：其中，则α_i的期望为

S44、更新q_β(β)：

其中，为关于分布q_w(w)的期望，因此β服从如下Gamma分布：其中则α_i的期望为

S45、对求导，可得令上式为0可得其中，<xx^T>＝μ_xμ_x^T+Φ_x；

S6、如果上述迭代过程满足终止条件停止迭代，否则返回S4进行下一次迭代。

经过上述操作，就完成了对稀疏信号和比特反转误差的双重估计。

下面将其他相关方法同本发明方法的算法性能对比分析，以进一步验证本发明的性能。

采用两种衡量指标来度量算法的性能。

一个是用来衡量稀疏信号的恢复准确性，叫做归一化均方误差(Normalized Mean Squared Error，简称NMSE)；

一个是用来衡量比特反转误差大小，叫做汉明误差(Hamming error).NMSE的定义为汉明误差的定义为

图1中m＝200,n＝100,K＝10，从该图可以看出相比那些忽视了比特反转误差的算法(BIHT,1-BCS)，本发明具有更大的性能优势；而相比那些考虑比特反转误差的算法，随着比特反转误差的增加，本算法的鲁棒性更强。图2中n＝100,K＝10,L＝10，即有10个比特反转误差，从该图可以看出，本发明随着测量个数m的增加，算法的性能相比其他算法有更大的提升。

综上，本发明方法是基于压缩感知的1比特量化误差估计方法，其将比特反转误差建模成一个稀疏信号，通过精心设计的迭代算法，更新算法各个相关参数，在不需要知道比特反转误差数目与位置的前提下，对稀疏信号和比特反转误差进行联合估计。在比特反转误差数目较多的情况下，本发明相比其他算法具有更高的鲁棒性，具有更大的性能优势。