一种基于神经网络预测的网络化控制系统故障检测方法与流程

本发明涉及一种基于神经网络预测的网络化控制系统故障检测方法，属电力系统和工业过程控制
技术领域：
。
背景技术：
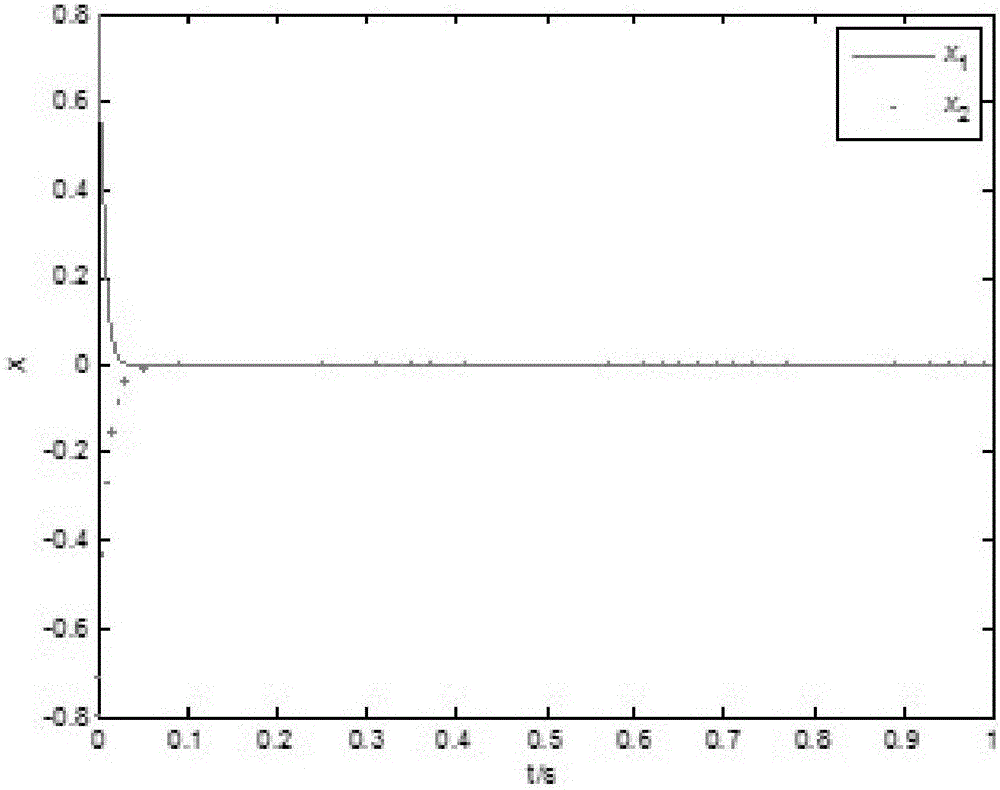
：网络化控制系统具有成本低，可靠性强，结构灵活等优点，被广泛应用于远程医疗、机器人、航空航天等领域，但网络的引入易产生时延丢包等问题，这些现象不仅会使系统性能下降，甚至使其运行不稳定[1,2]。随着网络规模逐渐扩大，系统的稳定性、安全性要求逐渐上升，因此网络化控制系统的故障检测问题受到专家学者们的广泛关注和研究，针对当前网络化控制系统运行中存在的问题，当前针对短时延网络化控制系统，通过构建Lyapunov函数并采用线性矩阵不等式(LMI)方法给出了系统稳定的充分条件；考虑存在时延和随机丢包的网络系统的滤波器设计问题，采用LMI的方法得到了系统均方指数稳定的充分条件；虽然这两种方法可一定程度上解决网络化控制系统运行的问题，但对于定理中出现的非线性项未做任何处理，其不等式约束是一个非严格的LMI，不能直接得到观测器参数，针对这一问题，当前又开发了基于传统的RBF神经网络对发生时延的网络化控制系统进行预测，可达到收敛速度快、唯一最佳逼近等优点，但中心矢量的选取具有任意性，造成系统性能不能达到满意的效果，因此不难看出，当前关于网络化控制系统运行存在的问题尚缺乏一种有效的解决及判定手段，为了提高网络化控制系统运行稳定性和可靠性，迫切需要开发一种全新的网络化控制系统故障检测方法。技术实现要素：本发明的目的是要提供一种基于神经网络预测的网络化控制系统故障检测方法。为达到上述目的，本发明是按照以下技术方案实施的：一种基于神经网络预测的网络化控制系统故障检测方法，包括如下步骤：第一步，构建RBF神经网络系统，首先构建存在传感器数据随机丢失和干扰的网络化控制系统数学模型，然后针对该网络化控制系统数学模型建立对系统输出进行预测的传统RBF神经网络，然后在传统RBF神经网络中引入至少一组隐含层函数、神经网络的误差代价函数及高效预测输出值运算函对传统RBF神经网络进行优化运算，并得到高精度的系统输出预判值；第二步，构建系统故障检测函数，基于第一步进行优化处理后的RBF神经网络系统，构建出系统故障检测函数，并同时获得系统增广数学模型；其中系统故障检测函数为：x‾(k+1)=Ax‾(k)+Bu^(k)+L[y′(k)-y‾(k)]u^(k)=β‾u‾(k)y‾(k)=α‾Cx‾(k)]]>其中，为存在传感器数据随机丢失和干扰的网络化控制系统数学模型的状态估计；为观测器的输出向量；为观测器的控制输入；为没有丢包发生时的控制输入；y′(k)为预测控制器的系统预测输出值，y′(k)＝(ψ(k)+1)y(k)，ψ(k)(0<ψ(k)<1)为预测输出值与实际输出值之间的误差；L为具有适当维数的观测器增益矩阵；系统增广数学模型为：z(k+1)=(AA1+BKβ(k)A2+BKβ‾A3+LCα‾A4+LCα(k)A5)z(k)+D1f(k)]]>其中，第三步，系统稳定性判定运算，判定系统稳定性时，1)需要通过：引理1Schur补：给定常数矩阵S、Q和A，若S、Q分别为对称正定矩阵，即S＝ST、Q＝QT，则ATSA+Q<0成立，当且仅当或引理2给定适维矩阵Y、H和E，若YT＝Y、FTF≤I，则Y+HFE+ETFTHT<0，当且仅当存在一个常数γ>0，使得Y+γHHT+γ-1ETE<0。为分析系统稳定性，由增广数学模型可得系统无故障时的观测器误差方程为：z(k+1)＝A′z(k)其中，2)由z(k+1)＝A′z(k)得：定理1对于给定标量γ(γ>0)，若存在适维矩阵H、S和Q(Q>0)，其中S为对称正定矩阵，使下面不等式成立：(B′-C′)Q[(B′)T-(C′)T][(A-Lα‾C)-B′]Q[(B′)T-(C′)T](B′-C′)Q[(A-Lα‾C)T-(B′)T]0<0]]>-S-1A′(A′)T-S<0]]>-S-1+γHHTA-Lα‾CB′(A-Lα‾C)T-S0(B′)T0-γI<0]]>且当0≤ψ(k)≤1时，观测器误差系统z(k+1)＝A′z(k)渐近稳定；3)证明：选取正定Lyapunov函数：V(k)＝zT(k)Sz(k)+eT(k)Qe(k)并可得：E{ΔV(k)}=E{V(k+1)-V(k)}=zT(k)[(A′)TS(A′)-S]z(k)+eT(k){[(A-Lα‾C)-B′]Q[(A-Lα‾C)T-(B′)T]-Q}e(k)+xT(k){[(A-Lα‾C)-B′]Q[(B′)T-(C′)T)]}e(k)-eT(k){(B′-C′)Q[(A-Lα‾C)T-(B′)T]x(k)+xT(k){(B′-C′)Q[(B′)T-(C′)T]}x(k)zT(k)[(A′)TS(A′)-S]z(k)+eT(k){[(A-Lα‾C)-B′]Q[(A-Lα‾C)T-(B′)T]-Q}e(k)]]>其中，若使观测器误差方程为渐近稳定，需使E{△V(k)}<0成立；首先，需使下式成立：(A′)TS(A′)-S<0[(A-Lα‾C)-B′]Q[(A-Lα‾C)T-(B′)T]-Q<0]]>由引理1，式(A′)TS(A′)-S<0可写为：-S-1A′(A′)T-S<0]]>则式(A′)TS(A′)-S<0小于0得证；由引理1，式(A′)TS(A′)-S<0可写为：-S-1(A-Lα‾C)-(B′)(A-Lα‾C)T-(B′)T-S<0]]>将式转化为如下形式：-S-1A-Lα‾C(A-Lα‾C)T-S+-100B′+{-100B′}T<0]]>由引理2可得：-S-1A-Lα‾C(A-Lα‾C)T-S+γ-10-10T+γ-10B′T0B′<0]]>结合Schur补引理，式可转化为则式小于0成立；4)接下来需使下式成立：x(k)e(k)T(B′-C′)Q[(B′)T-(C′)T][(A-Lα‾C)-B′]Q[(B′)T-(C′)T](B′-C′)Q[(A-Lα‾C)T-(B′)T]0x(k)e(k)<0]]>若式成立，则式成立，即E{△V(k)}<0成立，系统z(k+1)＝A′z(k)渐近稳定；5)由于式中存在-S-1+γHHT这一非线性项，因此定理1的条件式不再为LMI；通过添加一新的正定变量M(S-1>M)，由引理1可得则式中S-1用M代替，该问题就可转化为非线性最小化问题：若要直接求出式Tr(SM)中非线性最小化问题的全局最优解很困难，这里采用迭代算法进行求解：将式Tr(SM)最小化，同时对式进行验证，若式满足，就可终止最小化过程；其中迭代算法如下：首先确定变量：选择合适的充分小的初值γ0及一组合适的解(S0,M0,A’0,B’0,K’0,E’0,H0)，使它们均满足式和式并设k＝0。然后建立迭代关系式：求解关于式Tr(SM)和式的最小化问题：MinimizeTr(SkM+SMk)其中，令Sk+1＝S，Mk+1＝M。最后对迭代过程进行控制：若式满足，则适当增大γ0，接着回到第一步中确定合适解的部分；若式未在规定的迭代次数内满足，则退出，否则，设k＝k+1，退回到第二步。第四步，构建系统故障判定运算函数，首先构建出系统稳定性判定运算函数模型，然后在经过第三步的函数运行，并在系统运行稳定性符合运行要求后，利用系统故障判定运算函数进行系统故障运行分析；其中系统故障判定运算函数为：J(r,k)=[Σk=0LrT(k)r(k))]1/2Jth={E[Σk=0∞rT(k)r(k)]}1/2]]>其中，第一个式子表示系统的残差信号的评估函数，第二个式子表示系统的故障检测阈值；当评估函数大于阈值时，系统发生故障，反之，正常运行；L为仿真的时间段大小；残差向量r(k)＝Q[y(k)-y′(k)]为系统的实际输出与预测控制器的输出向量之差与输出权矩阵的乘积。进一步的，所述的第一步中的网络化控制系统数学模型为：x(k+1)=Ax(k)+Bu(k)+Df(k)y(k)=α(k)Cx(k)]]>其中：x(k)∈Rm、u(k)∈Rn、y(k)∈Rp和f(k)∈Rm分别为系统的状态、输入、输出和故障向量；A、B和D均为适维矩阵；α(k)∈R为满足Bernoulli0-1序列分布的变量，表示控制器到执行器通道的随机丢包情况，当α(k)＝0时，系统发生数据丢包现象，当α(k)＝1时系统无数据丢包发生：prob{α(k)=1}=E{α(k)}=α‾]]>prob{α(k)=0}=1-E{α(k)}=1-α‾]]>var{α(k)}=E{(α(k)-α‾)2}=(1-α‾)α‾]]>其中，数据包的丢包率一定且进一步的，所述的第一步中的隐含层函数的径向基函数为反常s型函数，其具体表达式为：hj=1/exp(-||yj-Tj||22cy2),j=1,2,3,4,5]]>其中，Tj为隐含层第j个结点的中心矢量；cj为隐含层第j个结点的基宽度参数。进一步的，所述的第一步中的神经网络的误差代价函数表达式为：E(k)＝0.5(y(k)-Y'(k))2其中，神经网络的实际输出与预测输出间误差为ζ(k)＝y(k)-y'(k)，并通过反馈校正对实际输出与预测输出间误差进行修正，令Y'(k)＝y'(k)+l*ζ(k)，其中l＝y(k)/y'(k)为修正系数。进一步的，所述的第一步中的高效预测输出值运算函数为：首先，运用迭代算法计算神经网络的中心矢量△Tj(k)、基宽度参数△cj(k)和连接权向量△wj(k)，其中η为学习效率：ΔTj(k)=-η∂E(k)∂Tj(k)=ηwjcj2Σi=15eihj(yj-Tj),Tj(k+1)=Tj(k)+ΔTj(k)]]>Δcj(k)=-η∂E(k)∂cj(k)=ηwjcj3Σi=15eihj(||yj-Tj||2),cj(k+1)=cj(k)+Δcj(k)]]>Δwj(k)=-η∂E(k)∂wj(k)=ηΣi=15eihj,wj(k+1)=wj(k)+Δwj(k)]]>然后，为得到更精确的预测输出值Y'(k)，添加调整参数α(0<α<1)对连接权向量△wj(k)进行修正，得到修正公式为：wj(k+1)＝wj(k)+α△wj(k)在预测过程中采用在线调整学习效率η的方法减少训练次数，若k时刻的实际输出值与预测输出值间误差过大，则在k+1时刻适当减小η使误差变小，从而得到更好的收敛性和预测效果，为故障观测器能够更快的检测出故障打下基础。进一步的，所述的第二步中，在进行系统故障检测函数运算时，需考虑控制器与执行器间存在丢包现象，并为克服这一问题，引入状态反馈控制函数，所述的状态反馈控制函数为：u‾(k)=-Kx‾(k)]]>u(k)=β(k)u‾(k)]]>其中，u(k)∈Rn为被控对象的控制输入；β(k)为控制器到执行器通道上的丢包情况，当β(k)＝0时，系统发生数据丢包现象；当β(k)＝1时，无数据丢包；β(k)∈R为满足Bernoulli0-1序列分布的变量：prob{β(k)=1}=E{β(k)}=β‾]]>prob{β(k)=0}=1-E{β(k)}=1-β‾]]>var{β(k)}=E{(β(k)-β‾)2}=(1-β‾)β‾]]>其中，数据包的丢包率一定且定义状态估计误差并得观测器的状态估计误差优化方程为：e(k+1)=(A-Lα‾C)e(k)+BK(β(k)-β‾)x(k)-BK(β(k)-β‾)e(k)-LC[(ψ(k)+1)α(k)-α‾]x(k)+Df(k).]]>本发明系统构成及计算过程简单，计算效率及运行精度具相对较高，通过采用改进的RBF神经网络的预测控制器有效预测出系统输出数据信息，从而有效抵消丢包给系统带来的不良影响，并在对得到的预测输出值采用反馈校正进行修正的基础上通过调整学习效率来使误差变小、训练次数降低，从而得到更好的收敛性和更快的预测速度。同时，当系统发生故障时，能够根据所设计的故障观测器及判定准则快速检测出故障的发生。附图说明下面结合附图和具体实施方式来详细说明本发明图1：隐含层RBF神经网络结构图；图2：引入观测器后系统的状态响应曲线图；图3：系统的预测输出与实际输出图；图4：系统故障检测结果仿真图；图5：本发明实施步骤流程图。具体实施方式为使本发明实现的技术手段、创作特征、达成目的与功效易于明白了解，下面结合具体实施方式，进一步阐述本发明。如图1—5所示，一种基于神经网络预测的网络化控制系统故障检测方法，包括如下步骤：第一步，构建RBF神经网络系统，首先构建存在传感器数据随机丢失和干扰的网络化控制系统数学模型，然后针对该网络化控制系统数学模型建立对系统输出进行预测的传统RBF神经网络，然后在传统RBF神经网络中引入至少一组隐含层函数、神经网络的误差代价函数及高效预测输出值运算函对传统RBF神经网络进行优化运算，并得到高精度的系统输出预判值；第二步，构建系统故障检测函数，基于第一步进行优化处理后的RBF神经网络系统，构建出系统故障检测函数，并同时获得系统增广数学模型；其中系统故障检测函数为：x‾(k+1)=Ax‾(k)+Bu^(k)+L[y′(k)-y‾(k)]u^(k)=β‾u‾(k)y‾(k)=α‾Cx‾(k)]]>其中，为存在传感器数据随机丢失和干扰的网络化控制系统数学模型的状态估计；为观测器的输出向量；为观测器的控制输入；为没有丢包发生时的控制输入；y′(k)为预测控制器的系统预测输出值，y′(k)＝(ψ(k)+1)y(k)，ψ(k)(0<ψ(k)<1)为预测输出值与实际输出值之间的误差；L为具有适当维数的观测器增益矩阵；系统增广数学模型为：z(k+1)=(AA1+BKβ(k)A2+BKβ‾A3+LCα‾A4+LCα(k)A5)z(k)+D1f(k)]]>其中，第三步，系统稳定性判定运算，判定系统稳定性时，1)需要通过：引理1Schur补：给定常数矩阵S、Q和A，若S、Q分别为对称正定矩阵，即S＝ST、Q＝QT，则ATSA+Q<0成立，当且仅当或引理2给定适维矩阵Y、H和E，若YT＝Y、FTF≤I，则Y+HFE+ETFTHT<0，当且仅当存在一个常数γ>0，使得Y+γHHT+γ-1ETE<0。为分析系统稳定性，由增广数学模型可得系统无故障时的观测器误差方程为：z(k+1)＝A′z(k)其中，2)由z(k+1)＝A′z(k)得：定理1对于给定标量γ(γ>0)，若存在适维矩阵H、S和Q(Q>0)，其中S为对称正定矩阵，使下面不等式成立：(B′-C′)Q[(B′)T-(C′)T][(A-Lα‾C)-B′]Q[(B′)T-(C′)T](B′-C′)Q[(A-Lα‾C)T-(B′)T]0<0]]>-S-1A′(A′)T-S<0]]>-S-1+γHHTA-Lα‾CB′(A-Lα‾C)T-S0(B′)T0-γI<0]]>且当0≤ψ(k)≤1时，观测器误差系统z(k+1)＝A′z(k)渐近稳定；3)证明：选取正定Lyapunov函数：V(k)＝zT(k)Sz(k)+eT(k)Qe(k)并可得：E{ΔV(k)}=E{V(k+1)-V(k)}=zT(k)[(A′)TS(A′)-S]z(k)+eT(k){[(A-Lα‾C)-B′]Q[(A-Lα‾C)T-(B′)T]-Q}e(k)+xT(k){[(A-Lα‾C)-B′]Q[(B′)T-(C′)T)]}e(k)-eT(k){(B′-C′)Q[(A-Lα‾C)T-(B′)T]x(k)+xT(k){(B′-C′)Q[(B′)T-(C′)T]}x(k)zT(k)[(A′)TS(A′)-S]z(k)+eT(k){[(A-Lα‾C)-B′]Q[(A-Lα‾C)T-(B′)T]-Q}e(k)]]>其中，若使观测器误差方程为渐近稳定，需使E{△V(k)}<0成立；首先，需使下式成立：(A′)TS(A′)-S<0[(A-Lα‾C)-B′]Q[(A-Lα‾C)T-(B′)T]-Q<0]]>由引理1，式(A′)TS(A′)-S<0可写为：-S-1A′(A′)T-S<0]]>则式(A′)TS(A′)-S<0小于0得证；由引理1，式(A′)TS(A′)-S<0可写为：-S-1(A-Lα‾C)-(B′)(A-Lα‾C)T-(B′)T-S<0]]>将式转化为如下形式：-S-1A-Lα‾C(A-Lα‾C)T-S+-100B′+{-100B′}T<0]]>由引理2可得：-S-1A-Lα‾C(A-Lα‾C)T-S+γ-10-10T+γ-10B′T0B′<0]]>结合Schur补引理，式可转化为则式小于0成立；4)接下来需使下式成立：x(k)e(k)T(B′-C′)Q[(B′)T-(C′)T][(A-Lα‾C)-B′]Q[(B′)T-(C′)T](B′-C′)Q[(A-Lα‾C)T-(B′)T]0x(k)e(k)<0]]>若式成立，则式成立，即E{△V(k)}<0成立，系统z(k+1)＝A′z(k)渐近稳定；5)由于式中存在-S-1+γHHT这一非线性项，因此定理1的条件式不再为LMI；通过添加一新的正定变量M(S-1>M)，由引理1可得则式中S-1用M代替，该问题就可转化为非线性最小化问题：若要直接求出式Tr(SM)中非线性最小化问题的全局最优解很困难，这里采用迭代算法进行求解：将式Tr(SM)最小化，同时对式进行验证，若式满足，就可终止最小化过程；其中迭代算法如下：首先确定变量：选择合适的充分小的初值γ0及一组合适的解(S0,M0,A’0,B’0,K’0,E’0,H0)，使它们均满足式和式并设k＝0。然后建立迭代关系式：求解关于式Tr(SM)和式的最小化问题：MinimizeTr(SkM+SMk)其中，令Sk+1＝S，Mk+1＝M。最后对迭代过程进行控制：若式满足，则适当增大γ0，接着回到第一步中确定合适解的部分；若式未在规定的迭代次数内满足，则退出，否则，设k＝k+1，退回到第二步。第四步，构建系统故障判定运算函数，首先构建出系统稳定性判定运算函数模型，然后在经过第三步的函数运行，并在系统运行稳定性符合运行要求后，利用系统故障判定运算函数进行系统故障运行分析；其中系统故障判定运算函数为：J(r,k)=[Σk=0LrT(k)r(k))]1/2Jth={E[Σk=0∞rT(k)r(k)]}1/2]]>其中，第一个式子表示系统的残差信号的评估函数，第二个式子表示系统的故障检测阈值；当评估函数大于阈值时，系统发生故障，反之，正常运行；L为仿真的时间段大小；残差向量r(k)＝Q[y(k)-y′(k)]为系统的实际输出与预测控制器的输出向量之差与输出权矩阵的乘积。进一步的，所述的第一步中的网络化控制系统数学模型为：x(k+1)=Ax(k)+Bu(k)+Df(k)y(k)=α(k)Cx(k)]]>其中：x(k)∈Rm、u(k)∈Rn、y(k)∈Rp和f(k)∈Rm分别为系统的状态、输入、输出和故障向量；A、B和D均为适维矩阵；α(k)∈R为满足Bernoulli0-1序列分布的变量，表示控制器到执行器通道的随机丢包情况，当α(k)＝0时，系统发生数据丢包现象，当α(k)＝1时系统无数据丢包发生：prob{α(k)=1}=E{α(k)}=α‾]]>prob{α(k)=0}=1-E{α(k)}=1-α‾]]>var{α(k)}=E{(α(k)-α‾)2}=(1-α‾)α‾]]>其中，数据包的丢包率一定且进一步的，所述的第一步中的隐含层函数的径向基函数为反常s型函数，其具体表达式为：hj=1/exp(-||yj-Tj||22cj2),j=1,2,3,4,5]]>其中，Tj为隐含层第j个结点的中心矢量；cj为隐含层第j个结点的基宽度参数。进一步的，所述的第一步中的神经网络的误差代价函数表达式为：E(k)＝0.5(y(k)-Y'(k))2其中，神经网络的实际输出与预测输出间误差为ζ(k)＝y(k)-y'(k)，并通过反馈校正对实际输出与预测输出间误差进行修正，令Y'(k)＝y'(k)+l*ζ(k)，其中l＝y(k)/y'(k)为修正系数。进一步的，所述的第一步中的高效预测输出值运算函数为：首先，运用迭代算法计算神经网络的中心矢量△Tj(k)、基宽度参数△cj(k)和连接权向量△wj(k)，其中η为学习效率：ΔTj(k)=-η∂E(k)∂Tj(k)=ηwjcj2Σi=15eihj(yj-Tj),Tj(k+1)=Tj(k)+ΔTj(k)]]>Δcj(k)=-η∂E(k)∂cj(k)=ηwjcj3Σi=15eihj(||yj-Tj||2),cj(k+1)=cj(k)+Δcj(k)]]>Δwj(k)=-η∂E(k)∂wj(k)=ηΣi=15eihj,wj(k+1)=wj(k)+Δwj(k)]]>然后，为得到更精确的预测输出值Y'(k)，添加调整参数α(0<α<1)对连接权向量△wj(k)进行修正，得到修正公式为：wj(k+1)＝wj(k)+α△wj(k)在预测过程中采用在线调整学习效率η的方法减少训练次数，若k时刻的实际输出值与预测输出值间误差过大，则在k+1时刻适当减小η使误差变小，从而得到更好的收敛性和预测效果，为故障观测器能够更快的检测出故障打下基础。本实施例中，所述的第二步中，在进行系统故障检测函数运算时，需考虑控制器与执行器间存在丢包现象，并为克服这一问题，引入状态反馈控制函数，所述的状态反馈控制函数为：u‾(k)=-Kx‾(k)]]>u(k)=β(k)u‾(k)]]>其中，u(k)∈Rn为被控对象的控制输入；β(k)为控制器到执行器通道上的丢包情况，当β(k)＝0时，系统发生数据丢包现象；当β(k)＝1时，无数据丢包；β(k)∈R为满足Bernoulli0-1序列分布的变量：prob{β(k)=1}=E{β(k)}=β‾]]>prob{β(k)=0}=1-E{β(k)}=1-β‾]]>var{β(k)}=E{(β(k)-β‾)2}=(1-β‾)β‾]]>其中，数据包的丢包率一定且定义状态估计误差并得观测器的状态估计误差优化方程为：e(k+1)=(A-Lα‾C)e(k)+BK(β(k)-β‾)x(k)-BK(β(k)-β‾)e(k)-LC[(ψ(k)+1)α(k)-α‾]x(k)+Df(k).]]>基于以上过程，下面对运算进行数据运算结果进行仿真验证：首先设定一个由以下参数构成的网络化控制系统：A＝[01；0-0.1],B＝[0；0.1],C＝[10].然后进行仿真验证，其中仿真验证步骤为：第一步，设系统初始状态为：[0.8-0.8]T。给定信号传输通道参数为：应用MATLAB编程求解得出观测器的增益矩阵为：L＝[-10.1385]T；然后再应用simulink仿真得到引入观测器后系统的状态响应曲线图，并由该图得到系统状态x1、x2趋于平衡状态时间在0.08s左右趋于平衡，而当前传统检测方法得到的系统趋于平衡状态则需要0.4s左右，因此运用本文方法得到的系统状态响应速度比文献[5]更具优势；第二部，当系统发生数据丢包时，给定信号传输通道参数为：此时应用MATLAB编程得到系统的预测输出与实际输出图，并从该图可得，采用基于改进的RBF神经网络的预测控制器对系统输出进行预测，预测误差在0s-0.04s之间；而运当前传统检测方法得到的估计误差在0s-0.25s之间，因此采用本文所述方法得到的预测误差更小，跟踪精度更高，说明将该预测方法应用到发生丢包的网络化控制系统中可有效抵消数据丢包给系统带来的不良影响，第三部，假设当系统发生阶跃型突变故障时，选定故障检测阈值ε＝0.15，得到的故障检测结果仿真图，并从该图得到，当系统在1s时刻左右发生故障时，残差迅速发生跳变，超过选取的检测阈值，快速有效地检测出故障的发生，检测结果较为理想，说明所设计的故障观测器是有效的。本发明系统构成及计算过程简单，计算效率及运行精度具相对较高，通过采用改进的RBF神经网络的预测控制器有效预测出系统输出数据信息，从而有效抵消丢包给系统带来的不良影响，并在对得到的预测输出值采用反馈校正进行修正的基础上通过调整学习效率来使误差变小、训练次数降低，从而得到更好的收敛性和更快的预测速度。同时，当系统发生故障时，能够根据所设计的故障观测器及判定准则快速检测出故障的发生。本行业的技术人员应该了解，本发明不受上述实施例的限制，上述实施例和说明书中描述的只是说明本发明的原理，在不脱离本发明精神和范围的前提下，本发明还会有各种变化和改进，这些变化和改进都落入要求保护的本发明范围内。本发明要求保护范围由所附的权利要求书及其等效物界定。当前第1页1 2 3