一种实现爆发式同步的环形耦合振子系统及方法与流程

本发明属于非线性动力学中耦合系统同步控制技术领域，涉及一种环形耦合振子系统中的爆发式同步自组织动力学行为分析与控制方法，具体地说，涉及一种实现爆发式同步的环形耦合振子系统及方法。

背景技术：

自然界中许多系统，由于存在非线性而出现复杂的动力学行为。具有复杂动力学行为的个体通过相互作用可以产生许多自组织现象，如各种形式的同步与振荡死亡等动力学行为。这些自组织现象的形成不仅与单元系统本身的内在属性有关，还与各个单元之间的相互作用方式和各个单元的空间分布有关。在自然界中，许多自然现象如桥梁与行人共振和动物群体的涌现等均与耦合振子系统的的爆发式同步有关。近年来，研究人员对如何控制或实现爆发式同步，以及从连续相变到非连续相变的控制等方面进行了卓有成效的探索并取得大量成果。

目前人们发现，在非均匀的复杂网络耦合系统中，通过引入频率的不均匀性，且使频率的值与节点的度正相关，可以使复杂网络系统产生爆发式同步。然而，在均匀的复杂网络中(如er网络或规则网络)，仅通过引入频率和度的相关性并不能产生爆发式同步。全局耦合网络中，有报道称通过引入耦合的不均性能够实现爆发式同步。然而，在均匀网络中，在没有频率和度的相关性情况下，是否可以实现爆发式同步的问题仍不清楚。耦合权重的引入对爆发式同步的影响是什么也不明确。

技术实现要素：

为了克服现有技术中存在的缺陷，本发明提供一种实现爆发式同步的环形耦合振子系统及方法，通过在在环形耦合振子系统中引入一种特定的频率空间分布，通过控制频率差权重系数和耦合强度等参数，使耦合振子系统从不相关态过渡到爆发式同步态。通过理论分析确定实现爆发式同步所需的耦合作用强度参数区间。并进一步拓展到有频率差权重耦合情形下，环形耦合振子系统中实现爆发式同步的参数区间的预测和实现。本发明采用的理论分析方法可以很好地确定环形耦合振子系统中从混合爆发式同步到经典爆发式同步的影响因素和参数区间。对更好地理解和实现在规则网络结构中的耦合振子系统的自组织动力学行为具有指导意义，并具有潜在的实用价值。其技术方案如下：

一方面，本发明提供了一种实现爆发式同步的环形耦合振子系统，包括：

s1：由n个近邻耦合的环形振子系统构成，单个振子单元采用具有不同振荡频率ωj的kuromoto振子，其动力学方程如公式(1)所示：

其中，θi、ωi分别是第i个振子的状态变量和频率值，ε、α分别是系统的实参数且分别代表振子之间的耦合强度和耦合频率差权重系数，采用周期边界条件，即θn+1＝θ1，θ0＝θn。

s2：s1所述的环形耦合振子系统的频率值采用一定的空间分布如公式(2)：

另一方面，本发明还提供了一种在上述环形耦合振子系统中实现爆发式同步控制的方法，包括：对s1所述环形耦合振子系统，当选定具有s2所述的频率空间分布时，在不同的耦合频率差权重系数α下，通过增加参数耦合强度ε，当耦合强度大于某一临界值时，耦合系统会达到混合爆发式同步或经典爆发式同步。

进一步地，包括以下步骤：

第一步：定义序参量：

其中<…>t表示对时间求平均，则序参量r在[0,1]之间取值，当r＝0时表示耦合振子相关性低，而当r＝1时表示耦合振子处于同步态。如果序参量r从0连续增加到1，表明耦合振子系统从部分同步逐渐走向同步；如果序参量r从0突然跳变到1，则耦合振子系统从不同步突然变到全部振子同步，称为爆发式同步。爆发式同步往往伴随着序参量的双稳和迟滞现象。

第二步：基于公式(1)，选择公式(2)中的频率空间分布，采用龙格库塔法进行数值仿真，对于任意耦合频率差权重系数α，采用准静态法，分别渐渐增加或减少系统的耦合强度ε，观察不同耦合强度下的序参量(公式(3))确定耦合系统(1)达到同步所需的临界耦合强度值εc，并实现爆发式同步状态。当α≤0时，耦合系统为混合式爆发式同步，当

0＜α≤1时，耦合系统为经典的爆发式同步，而当α＞1时，耦合系统为连续相变到同步态。

第三步：基于公式(1)，理论分析并确定耦合系统(1)在不同频率差权重系数α下，达到爆发式同步所需的临界耦合强度值。详细步骤如下：

(1)分析无耦合权重的情形，即α＝0，此时，方程(1)可以写成

其中ωj＝sin(θj+1-θj)+sin(θj-1-θj),j＝1,2,…,n,(5)

当n较大时，由公式(2)可知ωi+1≈ωi-1，若振子j与j-1和j+1同步时，sin(θj+1-θj)≈sin(θj-1-θj)，因此我们可以知道在同步边界处有：

ωj＝2sin(θj+1-θj)，(6)

若振子j同步到平均频率为则有则方程(4)可写成：

考虑到sin函数的有界性，|ωj|≤ωbws＝2，可得到某振子j会落入到同步集团的必要条件为：

但考虑到受边界上不同步振子的影响，达到同步的振子实际边界值ωbps要小于自然边界ωbws，为了确定部分同步时的实际边界值。数值计算了达到同步集团的振子数ns占全部振子数n的比ps随耦合强度ε的变化关系，表明：

由公式(2)中给定的频率分布，可知，最靠近平均频率的ns个振子先达到同步，所以有

其中，ωs表示同步集团边界上的振子的频率。

则

确定|ωj|的两个边界后，则可以由直线与边界的交点确定部分同步区和爆发式同步区域。

1)如果某个振子的频率值ωj使|ωj|≤ωbps,则振子处于部分同步区；2)如果某个振子的频率值ωj使|ωj|＞ωbws,则振子处于不同步的区域；3)如果某个振子的频率值ωj使ωbps≤|ωj|≤ωbws，则振子处于同步与不同步的过渡区；特别地，随着耦合强度的增加，当过渡区边上的不同步区的振子数逐渐减少，一旦减少到零，则过渡区的振子有可能突然变成同步振子，而出现爆发式同步。因这种爆发式同步前存在部分同步，所以称为混合式爆发同步。

(2)分析有耦合权重的情形，即α≠0的情形。此时，公式(4)中的ωj可写成：

ωj＝|ωj+1-ωj|^asin(θj+1-θj)+|ωj-1-ωj|^asin(θj-1-θj)，(12)

同样的，若振子j，j+1和j-1处于同步态，则有：

sin(θj+1-θj)≈sin(θj-1-θj)，此时

ωj≈(|ωj+1-ωj|^a+|ωj-1-ωj|^a)sin(θj-1-θj),(13)

由正弦函数的特性可知，ωbws＝|ωj+1-ωj|^α+|ωj-1-ωj|^α，(14)

ωbps＝0.75(|ωj+1-ωj|^α+|ωj-1-ωj|^α)，(15)

此时，耦合振子的状态可以由|ωj|的两个边界和直线与边界的交点的位置确定。具体确定方法与α＝0时一致。耦合权重系数α对两个边界ωbws和ωbps的形状产生影响，从而影响耦合振子在各种态的分布，即同步振子、不同步的振子，和过渡区振子的分布。

本发明通过理论分析确定实现爆发式同步所需的耦合作用强度参数区间，并进一步拓展到有频率差权重耦合情形下，环形耦合振子系统中实现爆发式同步的参数区间的预测和实现。本发明采用的理论分析方法可以很好地确定环形耦合振子系统中从混合爆发式同步到经典爆发式同步的影响因素和参数区间。对更好地理解和实现在规则网络结构中的耦合振子系统的自组织动力学行为具有指导意义。

附图说明

图1：耦合振子频率空间分布。

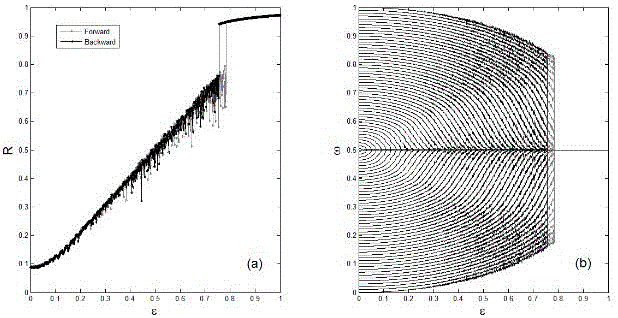
图2：(a)耦合振子同步序参量与耦合强度的关系图；(b)耦合振子平均频率与耦合强度的关系图。

图3：不同耦合权重系数下同步序参量与耦合强度的关系图。

图4：(a)-(c)不同耦合强度下，ωj曲线与全局同步办界和部分同步边界曲线；(d)所有耦合强度下，耦合振子状态分布状态图。

图5：不同耦合权重系数，不同耦合强度下，ωj曲线与全局同步办界和部分同步边界曲线。图6：不同耦合权重系数下，所有耦合强度对应的耦合振子状态分布状态图。

具体实施方式

下面结合附图和具体实施方式对本发明所述的技术方案做进一步地详细说明。

一种实现爆发式同步的环形耦合振子系统，包括：

s1：由n个近邻耦合的环形振子系统构成，单个振子单元采用具有不同振荡频率ωj的kuromoto振子，其动力学方程如公式(1)所示：

其中，θi、ωi分别是第i个振子的状态变量和频率值，ε、α分别是系统的实参数且分别代表振子之间的耦合强度和耦合频率差权重系数，采用周期边界条件，即θn+1＝θ1，θ0＝θn。

s2：s1所述的环形耦合振子系统的频率值采用一定的空间分布如公式(2)：

在上述环形耦合振子系统中实现爆发式同步控制的方法，包括：对s1所述环形耦合振子系统，当选定具有s2所述的频率空间分布时，在不同的耦合频率差权重系数α下，通过增加参数耦合强度ε，当耦合强度大于某一临界值时，耦合系统会达到混合爆发式同步或经典爆发式同步。具体地，包括以下步骤：

第一步：定义序参量：

其中<…>t表示对时间求平均，则序参量r在[0,1]之间取值，当r＝0时表示耦合振子相关性低，而当r＝1时表示耦合振子处于同步态。如果序参量r从0连续增加到1，表明耦合振子系统从部分同步逐渐走向同步；如果序参量r从0突然跳变到1，则耦合振子系统从不同步突然变到全部振子同步，称为爆发式同步。

第二步：基于公式(1)，选择公式(2)中的频率空间分布，采用龙格库塔法进行数值仿真，对于任意耦合频率差权重系数α，采用准静态法，分别渐渐增加或减少系统的耦合强度ε，观察不同耦合强度下的序参量(公式(3))确定耦合系统(1)达到同步所需的临界耦合强度值εc。并实现爆发式同步状态。如图2中分别给出了α＝0时,耦合振子的同步序参量r和各个振子的平均频率随耦合强度的变化关系。随着耦合强度从0逐渐增加，序参量r先线性增加，增加到某一临界值εc2时，突然跳变到1附近。随着耦合强度从1逐渐减少，序参量r则先保持在1附近，当耦合强度小于某一临界值εc1(εc1＜εc2)时，r突然跳变到某一较小的值上，此变化过程相比于经典的爆发式同步，因先有部分振子先达到同步，然后耦合强度大于某一临界值时，剩余的振子突然达到同步。称之为混合式爆发式同步。图3给出了α＝-1,-0.5,0.8,1.0,1.1时序参量r随耦合强度变化的关系。结果表明，不同的耦合频率差权重系数对耦合振子走向同步的过渡过程不同。当α≤0时，耦合系统为混合式爆发式同步，当0＜α≤1时，耦合系统为经典的爆发式同步，而当α＞1时，耦合系统为连续相变到同步态。

第三步：基于公式(1)，理论分析并确定耦合系统(1)在不同频率差权重系数α下，达到爆发式同步所需的临界耦合强度值。详细步骤如下：

(1)简单起见，先分析无耦合权重的情形，即α＝0，此时，方程(1)可以写成

其中，ωj＝sin(θj+1-θj)+sin(θj-1-θj),j＝1,2,…,n,(5)

当n较大时，由公式(2)可知ωi+1≈ωi-1，若振子j与j-1和j+1同步时，sin(θj+1-θj)≈sin(θj-1-θj)，因此我们可以知道在同步边界处有：

ωj＝2sin(θj+1-θj),(6)

若振子j同步到平均频率为则有则方程(4)可写成：

考虑到sin函数的有限性，|ωj|≤ωbws＝2，可得到某振子j会落入到同步集团的必要条件为：

但考虑到受边界上不同步振子的影响，达到同步的振子实际边界值ωbps要小于2，为了确定部分同步时的实际边界值。我们数值计算了达到同步集团的振子数ns占全部振子数n的比ps随耦合强度ε的变化关系，表明：

由公式(2)中给定的频率分布，可知，最靠近平均频率的ns个振子先达到同步，所以有

其中，ωs表示同步集团边界上的振子的频率。

则

确定|ωj|的两个边界后，则可以由直线与边界的交点确定部分同步区和爆发式同步区域。

1)如果某个振子的频率值ωj使|ωj|≤ωbps，则振子处于部分同步区；2)如果某个振子的频率值ωj使|ωj|＞ωbws，则振子处于不同步的区域；3)如果某个振子的频率值ωj使ωbps≤|ωj|≤ωbws，则振子处于同步与不同步的过渡区；特别地，随着耦合强度的增加，当过渡区边上的不同步区的振子数逐渐减少，一旦减少到零，则过渡区的振子有可能突然变成同步振子，而出现爆发式同步。因这种爆发式同步前存在部分同步，所以称为混合式爆发同步。如图4(a)-(c)图给出了不同耦合强度ε＝0.5,0.75,1.0时，边界值ωbps(部分振子同步边界)，ωbws(整个系统同步的边界)和直线的关系图。当ε＝0.5时，整个系统有同步的振子(1区)，不同步的振子(2区)，和过渡振子(3区)构成。当ε＝0.75时，同步振子区域扩大，不同步的振子消失，过渡振子依初始条件可能处于同步或不同步双稳态。当ε＝1.0时，不存在过渡振子，全部振子处于同步态。

由式(8)和式(11)可以确定，所有不同耦合强度下的三种振子类型的分布，即同步振子(白色)、不同步的振子(黑色)，和过渡振子(灰色)如图5(d)所示。

(2)下面分析有耦合权重的情形，即α≠0的情形。此时，公式(4)中的ωj可写成：

ωj＝|ωj+1-ωj|^asin(θj+1-θj)+|ωj-1-ωj|^asin(θj-1-θj)，(12)

同样的，若振子j，j+1和j-1处于同步态，则有：

sin(θj+1-θj)≈sin(θj-1-θj)，此时

ωj≈(|ωj+1-ωj|^a+|ωj-1-ωj|^a)sin(θj-1-θj),(13)

由正弦函数的特性可知，ωbws＝|ωj+1-ωj|^α+|ωj-1-ωj|^α,(14)

ωbps＝0.75(|ωj+1-ωj|^α+|ωj-1-ωj|^α)，(15)

此时，耦合振子的状态可以由|ωj|的两个边界和直线与边界的交点确定。耦合权重系数α的存在对两个边界的形状产生影响，从而影响耦合振子在各种态的分布，详见图5(a)-(f)给出不同的耦合权重系数α＝-1，-0.5，0.8，1.1，1.7和不同的耦合强度ε＝0.5，0.8，1.1下，耦合系统中各种态的分布情况。同样地，可以给出不同的耦合权重系数α＝-1，-0.5，0.8，1.0，1.1，1.7时，所有耦合强度对应的耦合振子系统的状态分布图。

以上所述仅为本发明的较佳实施方式，凡依本发明所做的均等变化与修饰，皆应属本发明的涵盖范围。