干摩擦阻尼隔振器等效阻尼确定方法与流程

本发明属于机械领域，具体涉及一种等效阻尼确定方法。

背景技术：

在非线性振动研究领域中，含有干摩擦阻尼的隔振系统受到了广泛关注。在机械结构中，干摩擦能够快速有效抑制外部干扰激励对系统产生的动力学响应，因而广泛应用于航空发动机叶片、晶体振荡器等结构的隔振中。

近些年，国内外学者对具有干摩擦的非线性隔振器构成的振动系统做了大量研究。例如白鸿柏等研究了粘性阻尼滞迟振子简谐激励响应的等效线性化计算方法；文献研究受简谐激励摩擦振子的周期运动行为，并对滑动过程进行求解和数值模拟。颜肖龙等从能量的角度将摩擦力等效为总体的粘性阻尼，对干摩擦阻尼的无谐振峰特性进行了研究。但是上述现有文献对摩擦力与阻尼、频率之间的对应关系均没有给出明确的等效方法。

技术实现要素：

本发明运用试验测试和理论仿真相结合的方法，将阻尼值根据频率分成多个不同的频段，并用优化方法获得不同频段的阻尼值，为干摩擦阻尼隔振器等效阻尼的确定寻找到了一条新的有效方法。

本发明提供了一种干摩擦阻尼隔振器等效阻尼确定方法，具有这样的特征，包括以下步骤：

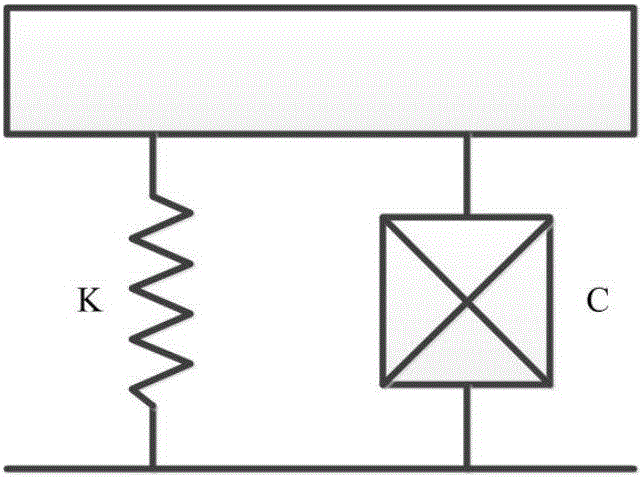
步骤1，建立干摩擦阻尼隔振器的理论模型，该隔振器的模型为包括刚度为K的弹簧和与所述弹簧并联的阻尼为C的一个弹簧阻尼单元；

步骤2，对加载有载荷M的所述隔振器进行扫频试验，分别测量所述隔振器的激励值和响应值并得到对应的隔振器激励曲线和隔振器响应曲线；

步骤3，进行有限元仿真，在有限元软件中建立所述隔振器的包括激励加载单元、弹簧阻尼单元以及载荷单元的有限元模型；

步骤4，在步骤3中的所述有限元模型中输入所述隔振器激励曲线进行有限元计算，得到有限元计算响应值以及对应的有限元计算响应曲线；

步骤5，阻尼优化，对所述有限元模型中的阻尼参数不断进行优化，对所述有限元计算响应曲线与所述隔振器响应曲线进行拟合,使得所述有限元计算响应曲线与所述隔振器响应曲线相吻合后得到最优的所述有限元计算响应曲线；

步骤6，从步骤5中得到的最优的所述有限元计算响应曲线中相应地得到所述有限元计算响应曲线的对应的优化的所述阻尼参数值，从而确定所述隔振器在载荷为M下的实际等效阻尼C。

在本发明提供的干摩擦阻尼隔振器等效阻尼确定方法中，还可以具有这样的特征，还包括：步骤7，根据步骤6中所述隔振器在载荷为M下的实际等效阻尼C，通过比例计算得到任意一个载荷为M×t下的理论等效阻尼C×t，其中，t为比例值，是一个常数。

另外，在本发明提供的干摩擦阻尼隔振器等效阻尼确定方法中，还可以具有这样的特征：其中，步骤1中所述阻尼C由干摩擦产生，其数值大小与受到的外部激励频率相关且随所述外部激励频率进行改变。

另外，在本发明提供的干摩擦阻尼隔振器等效阻尼确定方法中，还可以具有这样的特征：其中，步骤3中所述的有限元模型是使用商用软件HyperWorks软件中的CBush单元来模拟弹簧阻尼单元中的刚度K和阻尼C。

另外，在本发明提供的干摩擦阻尼隔振器等效阻尼确定方法中，还可以具有这样的特征：其中，步骤4中的所述隔振器激励曲线在所述有限元模型中的所述激励加载单元中输入。

另外，在本发明提供的干摩擦阻尼隔振器等效阻尼确定方法中，还可以具有这样的特征：其中，步骤4中获取有限元计算响应值的位置设置在所述弹簧阻尼单元与所述承载单元的共节点。

另外，在本发明提供的干摩擦阻尼隔振器等效阻尼确定方法中，还可以具有这样的特征：其中，步骤5中所述阻尼优化包括以下步骤：

S5-1,确定设计变量，所述设计变量为非线性的阻尼C在各关键频率点上的取值；

S5-2,建立目标函数,所述目标函数的表达式为：

S5-3,最小化目标函数,所述最小化目标函数的表达式为：

min(OBJ)，

其中y_i为所述有限元计算响应曲线上各对应点的位移响应，δ_i为所述隔振器响应曲线稀疏处理后各点对应的位移响应，i＝1，2，3，……n。

发明的作用与效果

根据本发明所涉及的干摩擦阻尼隔振器等效阻尼确定方法，包括步骤1，建立干摩擦阻尼隔振器的理论模型；步骤2，对加载有载荷的隔振器进行扫频试验，步骤3，进行有限元仿真；步骤4，在进行有限元计算，步骤5，阻尼优化，步骤6，确定隔振器的实际等效阻尼C。本发明所涉及的干摩擦阻尼隔振器等效阻尼确定方法运用了试验测试和理论仿真相结合的方法，通过扫频振动试验获取隔振器的隔振曲线，并将该试验隔振曲线作为优化目标，以各频段的阻尼为变量，用有限元仿真方法确定来干摩擦阻尼隔振器的等效阻尼，为干摩擦阻尼隔振器等效阻尼的确定寻找到了一条新的有效方法。

附图说明

图1是本发明的实施例中干摩擦阻尼隔振器的理论模型；

图2是本发明的实施例中试验中测得的隔振器激励曲线和隔振器响应曲线；

图3是本发明的实施例中在有限元软件中建立的隔振器有限元模型；

图4是本发明的实施例中优化前有限元计算响应曲线和试验响应曲线图；

图5是本发明的实施例中隔振器阻尼优化迭代曲线；

图6是本发明的实施例中优化后有限元计算响应曲线和试验响应曲线图；

图7是本发明的实施例中10kg试样有限元计算所得到的响应曲线与试验测得的响应曲线对比图；

图8是本发明的实施例中70kg试样有限元计算所得到的响应曲线与试验测得的响应曲线对比图；以及

图9是本发明的实施例中100kg试样有限元计算所得到的响应曲线与试验测得的响应曲线对比图。

具体实施方式

为了使本发明实现的技术手段、创作特征、达成目的与功效易于明白了解，以下实施例结合附图对本发明所提供的干摩擦阻尼隔振器等效阻尼确定方法作具体阐述。

实施例

步骤1，建立干摩擦阻尼隔振器的理论模型，该隔振器的模型为包括刚度为K的弹簧和与所述弹簧并联的阻尼为C的一个弹簧阻尼单元。

干摩擦阻尼隔振器的理论模型如图1所示，该隔振器实际可以简化为一个弹簧阻尼单元。由于隔振器力学模型的刚度K为弹簧的刚度，可以通过试验准确测出其数值，而模型中的阻尼C由干摩擦产生，其数值大小跟外部激励频率相关，是一个随频率变化的量。

在本实施例中，通过扫频振动试验获取隔振器的隔振曲线，并将该试验隔振曲线作为优化目标，以各频段的阻尼为变量，用有限元仿真方法确定干摩擦阻尼隔振器的阻尼。

步骤2，对加载有载荷M的所述隔振器进行扫频试验，分别测量所述隔振器的激励值和响应值并得到对应的隔振器激励曲线和隔振器响应曲线。

将一个质量为50kg的载荷安装于隔振器上部，隔振器的刚度为46N/mm，并有一定的干摩擦力。通过用一个已知信号进行激励，用本实施例确定干摩擦阻尼值，并用不同型号干摩擦阻尼隔振器对该方法进行验证。

对标称载荷为50kg的干摩擦阻尼隔振器进行扫频试验。将隔振器固定于振动台上，隔振器上部安装50kg的质量块作为负载，在振动台和质量块上各安装一个加速度计，测量激励值和响应值。

试验条件按正弦扫频振动进行，在5～16Hz频段为等位移激励，单振幅1mm；在16～176Hz频段为等加速度激励，加速度幅值为1g。

试验中测得的隔振器激励曲线和隔振器响应曲线如图2所示。

图2中位于中间的曲线3为隔振器激励信号曲线，曲线1为隔振器激励信号高限失效曲线，曲线2为隔振器激励信号高限预警曲线，曲线4为隔振器激励信号低限预警曲线，曲线5为隔振器响应曲线，曲线6为隔振器激励信号低限失效曲线。

激励的类型为5～16Hz时1g等加速度激励，16～176Hz为1mm等位移激励。

步骤3，进行有限元仿真，在有限元软件中建立所述隔振器的包括激励加载单元、弹簧阻尼单元以及承载单元的有限元模型。

在有限元软件HyperWorks中建立隔振器的有限元模型10，其中用CBush单元来模拟刚度和阻尼，该隔振器的有限元模型10如图3所示，隔振器的有限元模型10包括荷载11、弹簧阻尼单元12以及激励加载单元13。

实施例中，荷载11为50kg质量块。在底部三角处的激励加载单元13加载图2中的隔振器激励曲线，隔振器激励信号通过中间的弹簧阻尼单元12传递到上面的50kg质量块上，在弹簧阻尼单元12与荷载11共节点的位置J检测输出信号。因此，只要通过改变该弹簧阻尼单元12的刚度与阻尼值，即可获得与试验响应结果相近的响应曲线即可。

表1阻尼分段变化初值表

步骤4，在步骤3中的所述有限元模型10中输入所述隔振器激励曲线进行有限元计算，得到有限元计算响应值以及对应的有限元计算响应曲线。

在有限元软件HyperWorks中进行有限元计算，用弹簧阻尼单元模拟隔振器，但刚度阻尼的参数需要设定。在本实施例中，刚度为46N/mm，阻尼初始赋值如表1所示。

在有限元模型中输入图2的隔振器激励曲线进行有限元计算，得到有限元计算的响应曲线。

为了便于比较，将有限元计算的响应曲线和图2中的隔振器响应曲线放在一起(取5～110Hz)，如图4所示。从图4可以看出，有限元计算得到的响应曲线41和试验测得的隔振器响应曲线42有较大误差，必须对有限元模型的参数(干摩擦阻尼)进行优化。

步骤5，阻尼优化，对所述有限元模型中的阻尼参数不断进行优化，拟合所述有限元计算响应曲线与所述隔振器响应曲线,使得所述有限元计算响应曲线与所述隔振器响应曲线相吻合后得到最优的所述有限元计算响应曲线。

以试验测得的响应数据为目标，通过优化有限元模型中各关键频率点的阻尼值，使得有限元计算所得的响应结果与试验测得的响应结果总体差距最小。具体做法如下：

①设计变量

本次曲线拟合的设计变量为非线性的阻尼C在各关键频率点上的取值。初始值及变量的变化范围如表2所示。

表2设计变量取值表

②建立目标函数，其中y_i为所述有限元计算响应曲线上各对应点的位移响应，δ_i为所述隔振器响应曲线稀疏处理后各点对应的位移响应，i＝1，2，3，……n(频响分析结果每0.5Hz输出一个点，输出曲线上共有n个值)，实施例中，n＝191。

③最小化目标函数：min(OBJ)

根据目标函数，未优化之前目标值OBJ＝1.236。经过有限元HyperWorks优化计算后，目标值OBJ＝0.199。优化的迭代曲线如图5所示。

步骤6，从步骤5中得到的最优的所述有限元计算响应曲线中相应地得到所述有限元计算响应曲线的对应的优化的所述阻尼参数值，从而确定所述隔振器在载荷为M下的实际等效阻尼C。

优化后的有限元计算响应曲线与实际测量的隔振器响应曲线如图6所示，有限元结果与实验测量结果基本吻合。

优化之后的阻尼表如表3所示。

表3优化后阻尼表

步骤7，根据步骤5中所述隔振器在载荷为M下的实际等效阻尼C，通过比例计算得到任意一个载荷为M×t下的理论等效阻尼C×t，t为比例值，是一个常数。

为验证该方法的可推广性，针对不同型号的干摩擦阻尼隔振器的阻尼值进行简单计算。在本发明中以标称载荷分别为10kg、70kg和100kg的干摩擦阻尼隔振器为例进行验证。

本实施例叙述的优化方法可以得到标称载荷为50kg的各频段的等效阻尼值，将这些阻尼值分别表按照质量的比例分别得到10kg、70kg和100kg的阻尼值。

如表4所示，干摩擦阻尼隔振器的阻尼值大小一般与其标称载荷的大小成正比。

表4 10kg、70kg与100kg试样分段阻尼值

将表4所得到的阻尼值代入有限元模型，用同样的方法进行有限元计算，可分别得到标称载荷为10kg、70kg和100kg的干摩擦阻尼有限元计算响应曲线。有限元计算所得到的响应曲线与试验测得的隔振器响应曲线如图7、图8、图9所示。

从以上结果可以看出，有限元计算的响应曲线与实际测得的响应曲线基本吻合，这说明该优化方法可以简便准确地确定不同载荷的干摩擦阻尼隔振器的等效阻尼。

实施例的作用与效果

根据本实施例所涉及的干摩擦阻尼隔振器等效阻尼确定方法，包括步骤1，建立干摩擦阻尼隔振器的理论模型；步骤2，对加载有载荷的隔振器进行扫频试验，步骤3，进行有限元仿真；步骤4，在进行有限元计算，步骤5，阻尼优化，步骤6，确定隔振器的实际等效阻尼C。本实施例所涉及的干摩擦阻尼隔振器等效阻尼确定方法运用了试验测试和理论仿真相结合的方法，通过扫频振动试验获取隔振器的隔振曲线，并将该试验隔振曲线作为优化目标，以各频段的阻尼为变量，用有限元仿真方法确定来干摩擦阻尼隔振器的等效阻尼，为干摩擦阻尼隔振器等效阻尼的确定寻找到了一条新的有效方法。

另外，根据步骤6中所述隔振器在载荷为M下的实际等效阻尼C，通过比例计算得到任意一个载荷为M×t下的理论等效阻尼C×t，这极大地方便了技术人员获得任意载荷下的隔振器理论等效阻尼。

上述实施方式为本发明的优选案例，并不用来限制本发明的保护范围。