基于参数估计的压缩感知成像方法与流程

本发明属于雷达成像领域，涉及回波缺失情况下的逆合成孔径雷达成像方法。

背景技术：

逆合成孔径雷达(ISAR)的经典成像算法为距离-多普(RD)成像算法。主要原理为依据回波中不同散射点在距离向上的延时不同对距离单元进行分辨，在距离压缩的基础上，再依据不同方位向上相对雷达转动时所产生的多普勒频率的不同进行方位分辨。为获得较高的距离向分辨率通常发射大带宽的信号，而方位向分辨率则主要依赖于目标旋转的积累角度。RD算法的适用条件为目标小角度匀速转动，在此条件下目标上的散射点不会产生距离单元走动，此假设通常可以满足。RD算法的优点在于成像算法较为简单，计算量小，效率高。然而对于一些复杂的特殊情况，运用RD算法所得到的成像结果却并不理想。

压缩感知理论是近年来出现的新信号处理理论，已经得到广泛的研究。本次发明将运用压缩感知原理进行目标回波缺失情况下的雷达成像。依据压缩感知理论，如果信号是系稀疏的，那么就可以利用信号的可压缩性进行降维采样，通过非线性的优化处理过程就可以从测量值中高概率的恢复原始信号。雷达目标回波可看作目标上多个强散射点的回波叠加而成，因而满足压缩感知处理稀疏信号的条件。

当目标回波缺失时，运用RD算法所得的成像结果将会产生方位向散焦的结果，因而如何解决这一问题也是雷达成像中的研究课题之一。近年来出现的压缩感知理论便可用于稀疏雷达信号的恢复，进而可以较好地解决稀疏回波情况下的成像问题。

技术实现要素：

本发明的目的是为了解决目标回波缺失情况下，经典的RD算法对逆合成孔径雷达成像时无法获得高分辨图像的问题，而提出基于参数估计的压缩感知成像方法。

步骤一、将每个距离单元的回波信号表示为线性调频信号模型；

步骤二、根据线性调频信号模型构造压缩感知稀疏基矩阵，根据压缩感知稀疏基矩阵构造图像Θ(γ₀,α)；

步骤三、依据图像对比度的定义选取检索范围，结合压缩感知的成像方法进行参数估计，得到每个距离单元的回波信号的初始参考频率和每个距离单元的回波信号频率的倾斜度两个参数的估计值；

步骤四、根据每个距离单元的回波信号的初始参考频率和每个距离单元的回波信号频率的倾斜度两个参数的估计值，结合压缩感知的成像方法进行成像，得到回波缺失情况下目标的高分辨图像。

本发明的有益效果为：

基于参数估计的压缩感知成像算法，运用高效的恢复算法进行信号重构，以获得高分辨的目标雷达图像。

传统的距离-多普勒成像方法对于回波缺失情况下，得到的图像是散焦的，如图3；而本发明提出的方法可获得较高分辨率的目标图像。

本发明提出的算法对距离单元回波信号进行了模型重构，相比于传统的算法信号模型的精确度有所提高，如图4、5。

选取MG-25飞机数据，数据段大小为512×64，选取其中128段数据进行成像，结果如下图所示。

图3为传统的距离-多普勒成像方法得到的成像结果，由于目标的部分回波缺失，因而得到的图像散焦。

图4是本发明的方法获得的目标成像结果图；图5是本发明的方法获得的目标图像对比度检索结果图；可见，此时可清晰地看出目标形状，图像的分辨率得到了提高。

成像的质量可选择一定的指标进行定量的分析，可选用图像熵作为图像质量的评价指标。具体表达式如下：

式中，Θ为所得的图像矩阵，大小为M×N，其中图像熵越小则说明所得图像质量越好。传统RD方法所得图像熵为126.877，本发明方法所得图像熵为69.263。由此可见本发明方法得到的图像质量较好。

附图说明

图1是本发明的成像方法流程图；

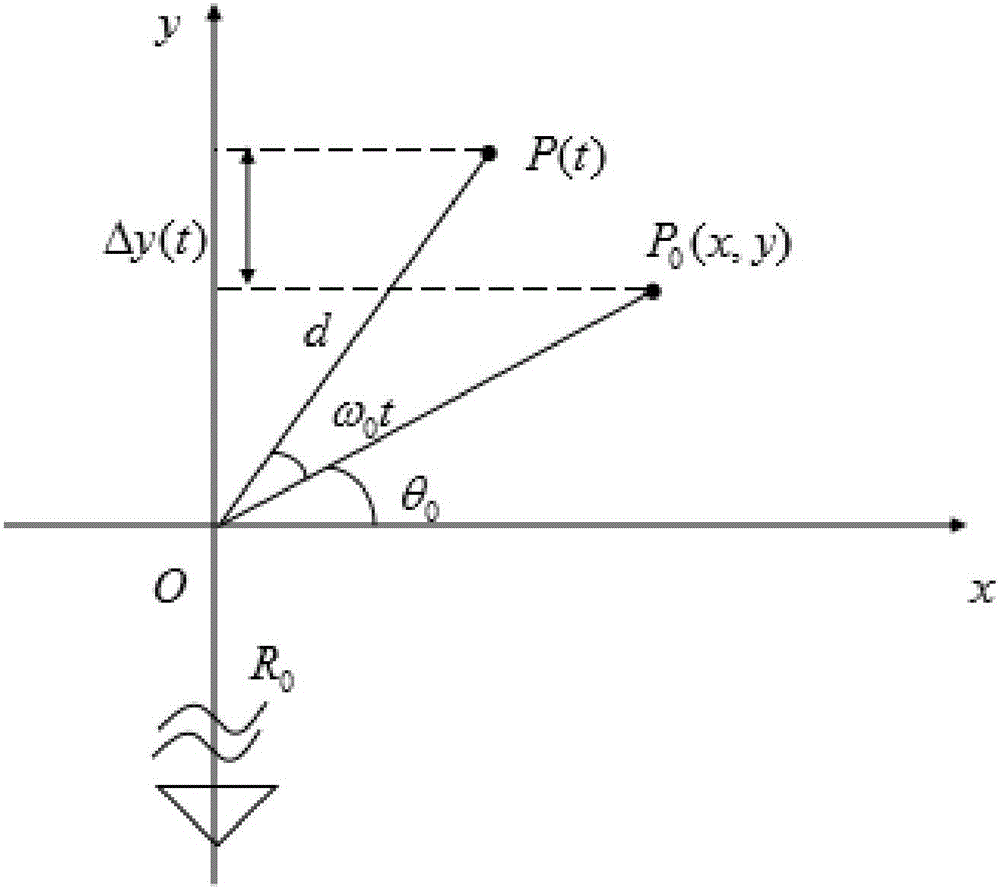
图2是本发明中目标散射点模型图，y为距离；P₀(x,y)为转动目标上的点，经过时间t运动到点P(t)；ω₀为角速度；P(t)为运动到的点；d为散射点到目标转动中心的距离；R₀为散射点到转动中心的距离；Δy(t)为两点间距离；θ₀为目标转角；

图3是传统的距离-多普勒成像方法得到的示意图；

图4是本发明的方法获得的目标成像结果图；

图5是本发明的方法获得的目标图像对比度检索结果图，image contrast为图像对比度数值，chirp rate reference为α频率参数，slope ofthe linear trend为γ₀频率倾斜度参数。

具体实施方式

具体实施方式一：结合图1说明本实施方式，本实施方式的基于参数估计的压缩感知成像方法具体过程为：

步骤一、将每个距离单元的回波信号表示为线性调频信号模型；

步骤二、根据线性调频信号模型构造压缩感知稀疏基矩阵，根据压缩感知稀疏基矩阵构造图像Θ(γ₀,α)；

步骤三、依据图像对比度的定义选取合理的检索范围，结合压缩感知的成像方法进行参数估计，得到每个距离单元的回波信号的初始参考频率和每个距离单元的回波信号频率的倾斜度两个参数的估计值；

步骤四、根据每个距离单元的回波信号的初始参考频率和每个距离单元的回波信号频率的倾斜度两个参数的估计值，结合压缩感知的成像方法进行成像，得到回波缺失情况下目标的高分辨图像。

具体实施方式二：本实施方式与具体实施方式一不同的是：所述步骤一中将每个距离单元的回波信号表示为线性调频信号模型；具体过程为:

如图2在较短的相干处理时间内，目标的转动速度可近似为常数。在这种情况下，转动目标上的点P₀(x,y)，经时间t以角速度ω₀运动到点P(t)，则两点间距离可表示为

Δy(t)＝d sin(θ₀+ω₀t)-d sinθ₀

＝x sinω₀t+y(cosω₀t-1)

式中，d为散射点到目标转动中心的距离。考虑到在很短的相干处理时间内，目标转角Δθ并不是很大，故式(1)可化简为

Δy(t)≈xω₀t

目标的多普勒频率可表示为

其中，R(t)和R₀分别为散射点到雷达和转动中心的距离。

y(t)＝d sin(θ₀+ω₀t)

＝x sinω₀t+y cosω₀t

为了对信号更加精确的表示将cosω₀t进行泰勒展开并保留前两项，即

线性调频信号模型的建立：

其中，μ_m为散射点的个数，σ_i为第i个散射点的反射系数，i取值为正整数；为第i个散射点的多普勒频率，j是虚数单位，j²＝-1；T为时间；γ_m为信号线性调频参数；s_m(T)为线性调频信号模型；

γ_m的具体表示形式如下

其中，Δr为两个连续距离单元间的距离，即为距离向分辨率；y为目标位置；为角速度；λ为波长；y₀为目标初始位置；N为距离单元个数，取值为正整数；γ₀为每个距离单元的回波信号的初始参考频率，α为每个距离单元的回波信号频率的倾斜度。

其它步骤及参数与具体实施方式一相同。

具体实施方式三：本实施方式与具体实施方式一或二不同的是：所述步骤二中根据线性调频信号模型构造压缩感知的稀疏基矩阵，根据压缩感知的稀疏基矩阵构造图像Θ(γ₀,α)；具体过程为：

依据线性调频信号模型，设K为多普勒频率的离散度，构造压缩感知的稀疏基矩阵如下：

其中，K为多普勒频率的离散度，f_k为离散多普勒频率，f_k＝k·f_r/K,k＝1,2,...,K，K取值为正整数；

则每个距离单元的回波表示为：

S_m＝Φ(γ_m)θ_m (4)

式中，S_m＝[s_m(1),s_m(2),...,s_m(N)]^T，θ_m为包含了所有散射点的反射系数；中每一列；图像Θ(γ₀,α)为所有距离单元θ_m的集合，即Θ(γ₀,α)＝{θ₁,θ₂,...,θ_M}。

其它步骤及参数与具体实施方式一或二相同。

具体实施方式四：本实施方式与具体实施方式一至三之一不同的是：所述步骤三中依据图像对比度的定义选取合理的检索范围，结合压缩感知的成像方法进行参数估计，得到每个距离单元的回波信号的初始参考频率和每个距离单元的回波信号频率的倾斜度两个参数的估计值；

依据图像对比度的定义选取合理的检索范围，结合压缩感知的成像方法进行参数估计，得到参数；具体过程为:

对于压缩感知的恢复算法，可采用工程上常用的正交匹配追踪算法(OMP)。图像Θ是关于参数γ₀和α的函数，即Θ(γ₀,α)。参数γ₀和α的选取直接影响成像结果。为了找到适合的参数，引入图像对比度的定义，具体如下

其中，<·>表示平均算子；图像对比度越大则说明成像质量越好。故在参数检索范围内，当图像对比度达到最大值时表明所选择的参数最合适，即

其它步骤及参数与具体实施方式一至三之一相同。

具体实施方式五：本实施方式与具体实施方式一至四之一不同的是：所述α＝0.65,γ₀＝-5.9。

其它步骤及参数与具体实施方式一至三之一相同。

采用以下实施例验证本发明的有益效果：

实施例一：

本实施例基于参数估计的压缩感知成像方法具体是按照以下步骤制备的：

本发明的具体实施方法如图1所示，其过程如下：

首先对回波信号进行距离压缩，然后进行运动补偿，包括包络对齐和相位校正两部分；从而建立目标距离单元的线性调频回波信号模型。运用压缩感知原理进行图像对比度检索进行信号参数估计，依据所得的估计参数进行成像，最后得到目标的高分辨图像。

回波信号模型及稀疏基矩阵的建立

目标进行距离向压缩和运动补偿后，所得信号的频域表示如下

其中T_p为脉冲宽度，f₀表示线性调频信号的初始频率，k为信号的调频斜率，R_Δ＝R_t-R_ref为目标上的点与参考点间的距离。

假设目标的转动速度近似为常数，则第m个距离单元回波信号多普勒频率的变化率可表示为

因而第m个距离单元内的回波信号可表示为

依据回波信号模型，对其进行离散则可构建稀疏基矩阵如下

二、正交匹配追踪算法及图像对比度检索

运用OMP算法可较快的对距离单元内的信号进行恢复，得到目标图像。依据图像对比度的定义，可在参数检索范围内进行搜索，采用OMP算法得到图像并算出检索范围内每幅图像的对比度，进而对参数估计。得到估计的参数后则可得到最优的成像结果。下面简述OMP算法的重构步骤：

设原始信号为x，重构矩阵为Φ，观测值为y，信号稀疏度为K，且设重构信号为观测值y的估计值为残差信号为r。开始，迭代次数l＝0，则残差值为观测值，即r⁰＝y，重构信号x⁰＝0，表示选择的原子索引集OMP算法的具体步骤可以表示为：

1、计算残差r与重构矩阵Φ中每一个列向量的内积值gⁿ＝Φ^Tr^n-1；

2、找出gⁿ中值最大的元素，k＝argmax|gⁿ[i]|,i∈{1,2,...,N}；

3、更新索引集Γⁿ＝Γ^n-1∪{k}及原子集合

4、利用最小二乘求得近似解

5、更新残差rⁿ＝y-Φxⁿ；

6、判断是否满足预设的迭代停止条件，若满足则令r＝rⁿ，并且输出和rⁿ，否则转到步骤1继续迭代直至满足条件。

基于参数估计的压缩感知成像算法的具体过程

1.选定参数{γ₀,α}的检索范围，计算每个距离单元的γ_m。

2.构建稀疏基矩阵Φ(γ_m)∈C^N×K。

3.通过OMP算法重构θ_m，进而得到图像Θ(γ₀,α)。

4.依据所选参数范围进行检索，找出满足条件的参数{γ₀,α}。

5.用检索到的参数{γ₀,α}进行成像。

本发明还可有其它多种实施例，在不背离本发明精神及其实质的情况下，本领域技术人员当可根据本发明作出各种相应的改变和变形，但这些相应的改变和变形都应属于本发明所附的权利要求的保护范围。