一种计及对潮流影响的电动汽车充电站电气接入点的选择方法与流程
本发明涉及电动汽车充电负荷在空间上合理布局领域,特别是涉及一种计及对潮流影响的电动汽车充电站电气接入点的选择方法。
背景技术:
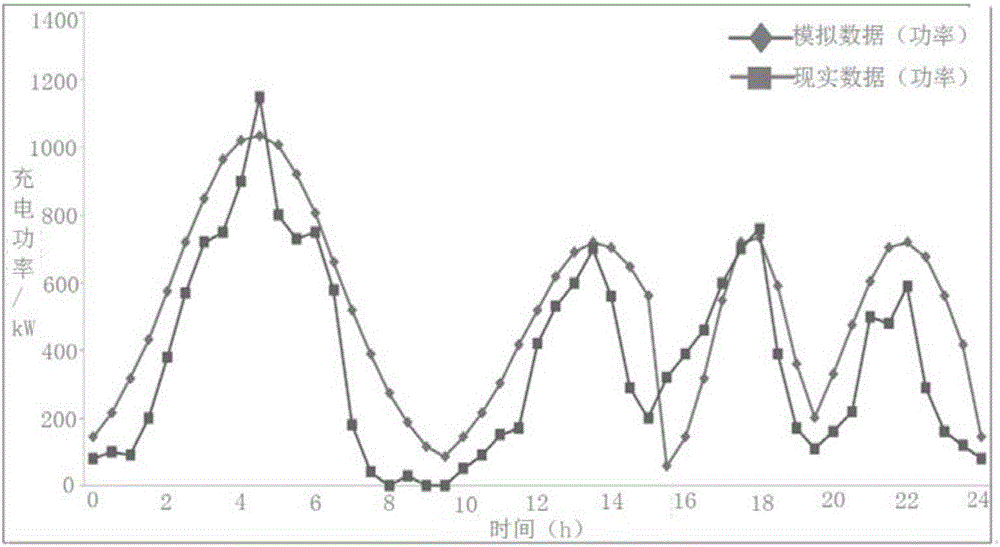
:作为解决传统化石能源短缺、城市环境污染加剧、全球气候变暖的一种有效途径,电动汽车正在全世界范围内受到广泛的关注,目前已逐渐成为各国政府、汽车生产企业、广大消费者关注的焦点。现有研究表明,大量电动汽车的充电负荷会对电力系统运行的安全性、经济性和电能质量产生明显影响,因而需要对充电负荷进行合理引导和调控。影响电动汽车充电负荷的因素包括电池初始荷电状态、起始充电时刻、充电方式、汽车出行规律等,考虑到一些影响因素具有随机性,一般采用概率表分布模拟充电负荷,为此,就需要比较准确的模拟充电负荷的分布特性。针对电动汽车充电负荷在空间上合理布局问题,现有研究主要围绕充电站的选址和定容展开,而就如何确定充电站在所属区域配电系统中的电气接入点则尚未论及。技术实现要素:本发明的目的是针对现有技术的不足,提供一种计及对潮流影响的电动汽车充电站电气接入点的选择方法。本发明的目的是通过以下技术方案实现的:一种计及对潮流影响的电动汽车充电站电气接入点的选择方法,包括以下步骤:步骤一:依据电动汽车出行统计数据的拟合结果,得到不同时段电池初始荷电状态和起始充电时刻的概率分布特性,进而建立电动出租车充电负荷的概率模型p(t);具体为:(1.1)依据电动出租车日行驶里程统计数据拟合结果,并经Jarque-Bera正态分布假设检验,电动出租车日平均行驶里程概率密度函数f(s)表示为:式中:s表示电动出租车的日平均行驶里程(km),t表示充电时间,μ和σ分别表示均值和标准差。(1.2)引入时间间隔系数β(以天为单位)来模拟相邻两次充电间的时间间隔,假设电池荷电量的下降与其日平均行驶里程成线性关系,则下一次充电开始时电池初始荷电状态Isoc和日平均行驶里程s的约束关系如下:式中:M表示电池满电量情况下最大行驶里程。根据式(1)-(2),由连续型随机变量函数的概率密度分布定理可导出,对应上述两个时段的电动出租车初始荷电状态概率密度函数如下式所示:式中:μs和σs分别表示对应日行使里程(s)分布特性的均值和标准差;f(Isoc)表示电池初始荷电状态概率密度函数。(1.3)确定特定充电方式下对应的充电持续时间Z,单位为小时。一天内充电时刻划分的颗粒度用相邻两充电时刻的时间间隔I表示,单位为小时。假设一天划分为n个时间段,则:n取整数且n≥1(14)对任意t时刻充电概率有影响的之前时间点共有Q个,则:当I>Z,则Q=0;当I≤Z,则Q=[Z/I](取整)。(1.4)根据电池初始荷电状态分布特性和开始充电时刻分布特性,一天内某时刻t电动出租车充电概率p(t)表示为:式中:t-z表示t时刻前第z个时刻点。步骤二:根据电动出租车充电负荷的概率模型p(t),以节点电压偏差百分数和支路有功功率损耗增量百分数为基础,构造用于评估电动汽车充电站对配电系统潮流影响的综合指标,结合步骤1获得的电动出租车充电负荷的概率模型p(t),采用牛顿-拉夫逊潮流算法,确定电动汽车充电站的电气接入点。具体为:(2.1)系统节点电压偏差百分数和支路有功功率损耗增量百分数分别如下式所示:式中:Δum,k表示配电系统中节点k在电动汽车充电站充电负荷接入后引起的电压偏差百分数;Δploss,l表示配电系统支路l在电动汽车充电站充电负荷接入后引起的有功功率损耗增量百分数;um,k和um,k,EV分别表示电动汽车充电站充电负荷接入配电系统前后节点k的电压幅值;ploss,l和ploss,l,EV分别表示电动汽车充电站充电负荷接入配电系统前后支路l上的有功功率损耗;pl表示充电负荷接入前配电系统支路l的传输有功功率。(2.2)各节点电压偏差平均值和各支路有功功率损耗增量平均值分别表示为和其中,N、L分别表示电动汽车充电站所属服务区域配电系统电气节点总数和支路总数。潮流影响综合评价指标如下式所示:(2.3)根据潮流影响综合评价指标值最小原则,电动汽车充电站在所属服务区域配电系统内最优电气接入点kop,EV的选择依据如下式所示:其中,kEV表示电动汽车充电站充电负荷在所属服务区域配电系统内的电气接入点,kop,EV表示基于潮流影响综合最小的最优电气接入点。本发明通过充分的统计数据以及适当的概率分布对初始荷电状态、起始充电时间等充电影响因素随机特性进行了模拟,提高了电动汽车充电负荷概率模型的精度。有益效果主要为:(1)依据车辆出行统计数据拟合结果获得初始荷电状态和起始充电时刻分布特性,考虑了充电延续性对充电负荷在时间维度上的累加效应,实现对充电负荷更准确模拟。(2)兼顾了节点电压偏差和支路功率损耗增量的双重影响,通过定义节点电压偏差百分数和支路有功功率损耗增量百分数,提出了电动汽车充电站对配电系统潮流影响的综合评价指标,给出了充电站最优电气接入点的选择方法。(3)配电系统在开环运行状态下,充电站充电负荷越大,对系统潮流的影响越大;在同一负荷水平下,充电站充电负荷在系统不同电气节点接入时,对系统潮流的影响不同;系统闭环运行状态下充电对系统潮流的影响要比开环小。本方法的提出也可用于电动汽车充电站在同一服务区域内不同电气设计方案的比较,由此确定基于潮流影响最小的充电站最优设计方案。附图内容图1为充电负荷估算值与实际值的对比。图2为IEEE33节点配电系统拓扑图。图3为基于潮流影响最小化的充电站电气接入点选择算法流程。图4为不同负荷水平下充电站充电负荷在系统不同电气节点接入时对系统潮流影响综合评价指标值。图5为不同运行方式下负荷水平为level1的充电站在系统不同电气节点接入时的潮流影响综合评价指标值。图6为负荷水平为level1时充电站充电负荷在系统不同电气节点接入时对系统节点电压幅值影响。具体实施方式本发明通过分析得到不同时段电动汽车电池初始荷电状态和起始充电时刻的概率分布特性,提出了用于评估电动汽车充电站对配电系统潮流影响的综合指标,以此确定充电站的电气接入点。具体包括以下步骤步骤一:依据电动汽车出行统计数据的拟合结果,得到不同时段电池初始荷电状态和起始充电时刻的概率分布特性。进而建立电动出租车充电负荷的概率模型p(t);依据电动出租车日行驶里程统计数据拟合结果,并经Jarque-Bera正态分布假设检验,电动出租车日平均行驶里程概率密度函数f(s)表示为:式中:s表示电动出租车的日平均行驶里程(km),t表示充电时间,μ和σ分别表示均值和标准差。引入时间间隔系数β(以天为单位)来模拟相邻两次充电间的时间间隔,假设电池荷电量的下降与其日平均行驶里程成线性关系,则下一次充电开始时电池初始荷电状态Isoc和日平均行驶里程s的约束关系如下:式中:M表示电池满电量情况下最大行驶里程。根据式(1)-(2),由连续型随机变量函数的概率密度分布定理可导出,对应上述两个时段的电动出租车初始荷电状态概率密度函数如下式所示:式中:μs和σs分别表示对应日行使里程(s)分布特性的均值和标准差;f(Isoc)表示电池初始荷电状态概率密度函数。考虑充电的延续性,需要确定特定充电方式下对应的充电持续时间,这里用Z表示,单位为小时。一天内充电时刻划分的颗粒度用相邻两充电时刻的时间间隔I表示,单位为小时。假设一天划分为n个时间段,则:n取整数且n≥1(24)定义对任意t时刻充电概率有影响的之前时间点共有Q个,则:当I>Z,则Q=0;当I≤Z,则Q=[Z/I](取整)。考虑充电持续性对充电负荷在时间维度的累加效应,根据电池初始荷电状态分布特性和开始充电时刻分布特性,一天内某时刻t电动出租车充电概率p(t)表示为:式中:t-z表示t时刻前第z个时刻点。这样,某时刻t单台电动汽车的充电负荷期望值d(t)可用下式求取:d(t)=p(t)P(27)式中:P表示单辆电动汽车的充电功率。由大数定律可知,假设N台电动汽车之间的充电行为彼此独立则N台电动汽车的充电负荷期望收敛于单台电动汽车充电负荷的N倍。由此就可以求得一天内不同时刻一定数量电动汽车的充电负荷。步骤二:根据电动出租车充电负荷的概率模型p(t),以节点电压偏差百分数和支路有功功率损耗增量百分数为基础构造用于评估电动汽车充电站对配电系统潮流影响的综合指标结合步骤1获得的电动出租车充电负荷的概率模型p(t),采用牛顿-拉夫逊潮流算法,确定电动汽车充电站的电气接入点。(2.1)所述系统节点电压偏差百分数和支路有功功率损耗增量百分数分别如下式所示:式中:Δumk表示配电系统中节点k在电动汽车充电站充电负荷接入后引起的电压偏差百分数;Δplossl表示配电系统支路l在电动汽车充电站充电负荷接入后引起的有功功率损耗增量百分数;umk和umkEV分别表示电动汽车充电站充电负荷接入配电系统前后节点k的电压幅值;plossl和plosslEV分别表示电动汽车充电站充电负荷接入配电系统前后支路l上的有功功率损耗;pl表示充电负荷接入前配电系统支路l的传输有功功率。Δumk和Δplossl都是用来表示充电负荷接入后引起的配电系统潮流变化以上两式具有如下性质:1)两者都做了标准化处理没有量纲并用百分数的形式表示;2)两者的大小均与潮流影响的大小成正比且充电负荷增减时两者的变化趋势是一致的。(2.2)为了全面反映充电站充电负荷对系统潮流的影响评价指标的计算应计及系统所有节点和各条支路采用各节点电压偏差平均值和各支路有功功率损耗增量平均值分别表示为和其中N、L分别表示电动汽车充电站所属服务区域配电系统电气节点总数和支路总数。为了综合反映充电站充电负荷对系统潮流的影响既考虑节点电压偏差又计及支路功率损耗基于潮流影响综合最小原则来选择充电站最优电气接入点定义潮流影响综合评价指标如下式所示:依据式(8)和(9)的性质综合评价指标能够有效反映充电对系统潮流的影响兼顾了节点电压偏差和支路功率损耗的变化综合指标中两个分量具有一致性变化趋势任意分量及其组合的变化都能够反映在综合指标上综合指标大小与潮流影响的大小成正比。整体上讲综合指标越小充电对系统潮流的影响越小反之则相反。这里用kEV表示电动汽车充电站充电负荷在所属服务区域配电系统内的电气接入点kop,EV表示基于潮流影响综合最小的最优电气接入点。根据潮流影响综合评价指标值最小原则电动汽车充电站在所属服务区域配电系统内最优电气接入点kop,EV的选择依据如下式所示:下面结合实施例对本发明作进一步说明。参数设置:假设电动出租车一天内需充电2次,均采用快速充电方式假定每次充电持续时长1小时,电动出租车充电功率取值32kW电池满电量的最大行驶里程300km。为了与实际数据做同一数量级的对比验证充电站电动出租车的数量取45台,一天内以半小时为时间间隔,并且假定配电系统容量充足。以IEEE33节点配电系统为例节点基准电压12.66kV基准容量取10MVA系统接线图和系统参数分别见的图2和表1。根据配电系统闭环结构、开环运行的常态当系统联络开关全部断开时采用牛顿-拉夫逊潮流算法计算得出电动出租车充电站充电负荷未接入配电系统时系统各节点电压、各支路有功功率损耗及传输功率如表2、3所示。表1IEEE33节点系统参数表2充电负荷未接入系统时各节点电压幅值节点电压(p.u.)节点电压(p.u.)节点电压(p.u.)11.05120.984231.03121.047130.979241.02431.034140.977251.02141.027150.976261.00151.02160.976270.99861.002170.975280.98770.999180.999290.9880.995191.047300.97690.99201.043310.972100.985211.042320.972110.985221.042330.971表3充电负荷未接入系统时各支路有功功率损耗及传输功率根据给定的算例场景及初始条件采用牛顿-拉夫逊潮流算法计算充电站充电负荷在所属配电系统不同电气节点接入时对系统潮流的影响基于潮流影响综合评价指标最小原则确定充电站最优电气接入点具体流程示意图如图3所示。为了说明基于潮流影响最小化的充电站电气接入点选择方法,假设充电站充电负荷分别从节点编号为3、5、15、22、26、33节点接入系统。需要指出,这里所提及的电气接入节点,均指符合电动汽车充电站专用变压器电压等级的节点,且节点容量充足。根据算例初始条件和给出的算法流程,在配电系统开环运行的情况下,计算得出电动汽车充电站负荷水平为level1时在不同节点接入下充电站充电负荷对系统潮流的影响如表4所示。表4负荷水平为level1时充电站充电负荷对系统潮流影响同理也可以计算得出负荷水平分别为level2、level3时充电站充电负荷对系统潮流的影响。根据潮流影响综合评价指标的定义可以计算得出不同负荷水平下充电站充电负荷在系统不同电气节点接入时对系统潮流影响的综合评价指标值如图4所示。由潮流影响计算结果可知在负荷水平为level1时当充电站充电负荷从系统电气节点3接入时潮流影响综合评价指标值最小其值为0.0033。随着充电站规模扩大当负荷水平分别为level2、level3时相应的潮流影响综合评价指标最小值分别为0.00721、0.0106此时对应的充电站电气接入节点也都是节点3。考虑到在故障状态或转供电情况下配电系统可能处于闭环运行状态。依据上述方法同理可以计算出配电系统闭环运行状态下当充电站负荷水平为level1时充电负荷在不同电气节点接入时对系统潮流的影响与开环状态下同一负荷水平的潮流影响结果的比较见图5所示。计算结果显示配电系统在开环运行状态下当充电站从节点15接入时对系统潮流影响最大相应的潮流影响综合评价指标值是闭环运行时最大值的1.82倍而从节点3接入无论系统运行状态如何潮流影响都是最小的。总体而言在系统闭环运行状态下充电站对系统潮流的影响要比开环小。通过充分的统计数据以及适当的概率分布对初始荷电状态、起始充电时间等充电影响因素随机特性进行了模拟提高了电动汽车充电负荷概率模型的精度。在此基础上以IEEE33节点配电系统为例基于对潮流影响最小化为目标确定充电站在配电系统最优电气接入节点。该方法依据车辆出行统计数据拟合结果获得初始荷电状态和起始充电时刻分布特性考虑了充电延续性对充电负荷在时间维度上的累加效应实现对充电负荷更准确模拟。并且,兼顾了节点电压偏差和支路功率损耗增量的双重影响通过定义节点电压偏差百分数和支路有功功率损耗增量百分数提出了电动汽车充电站对配电系统潮流影响的综合评价指标给出了电动汽车充电站最优电气接入点的选择方法。配电系统在开环运行状态下充电站充电负荷越大对系统潮流的影响越大;在同一负荷水平下充电站充电负荷在系统不同电气节点接入时对系统潮流的影响不同;系统闭环运行状态下充电对系统潮流的影响要比开环小。当前第1页1 2 3
相关技术
网友询问留言
已有0条留言
- 还没有人留言评论。精彩留言会获得点赞!
1