基于自适应终端滑模控制的汽车线控转向控制方法与流程

本发明属于车辆工程领域的线控转向技术，具体涉及一种基于自适应终端滑模控制的汽车线控转向控制方法。

背景技术：

滑模控制是最强大的非线性控制方法之一。由于在滑模平面上，滑模控制对参数变化和外部干扰具有不变性，滑模控制已经成功应用于许多实用的机电系统。然而传统的基于超平面的线性滑模控制，跟踪误差不能在有限时间内收敛，并且在闭环系统中存在抖振现象。

文献“b.beltran,t.ahmed-ali,andm.benbouzid,‘high-ordersliding-modecontrolofvariable-speedwindturbines,’ieeetrans.ind.electron.,vol.56,no.9,pp.3314–3321,sep.2009.(b.beltran,t.ahmed-ali,andm.benbouzid.变速风力发电机的高阶滑模控制方法.ieee工业电子.2009,56(9):3314-3321)”中提出了高阶滑模控制技术，能够减少抖振并保持经典滑模控制的鲁棒性和高控制精度。然而，设计这一滑模控制系统所需的不确定参数和扰动值的界限在实际应用中很难预先获得。

文献“k.nam,h.fujimoto,andy.hori,‘lateralstabilitycontrolofin-wheel-motor-drivenelectricvehiclesbasedonsideslipangleestimationusinglateraltireforcesensors,’ieeetrans.veh.technol.,vol.61,no.5,pp.1972–1985,jun.2012.(k.nam,h.fujimoto,andy.hori.基于使用侧向轮胎力传感器进行侧滑角估计的轮内电机驱动的电动车辆的侧向稳定性控制.ieee车辆技术.2012,61(5):1972-1985)”中提出了轮胎扰动转矩在线估计的pd控制技术，能够减轻变化参数和扰动的影响。但是运用该技术的线控转向车辆在遇到道路条件频繁变化的情况时，无法确保稳定的转向性能。

综上所述，现有的汽车线控转向系统控制方法存在如下问题：

1、传统的基于超平面的线性滑模控制，跟踪误差不能在有限时间内收敛，并且闭环系统存在抖振现象；

2、高阶滑模控制系统所需的不确定参数和干扰值的界限在实际应用中很难预先获得；

3、在线估计的pd控制技术无法在道路条件频繁变化的情况下保证稳定的转向性能。

因此，本领域需要一种能够实现在汽车线控转向系统中不需要提前知道系统参数和道路条件，同时又能够克服道路条件变化对系统产生的影响的具有鲁棒性的控制方法，来提升车辆的转向性能。

技术实现要素：

本发明要解决的技术问题为克服现有技术中控制器的跟踪误差无法在有限时间内收敛以及需要提前知道系统参数和路况信息的不足，提供了一种用于线控转向车辆的新型自适应终端滑模控制方案。

本发明的目的是这样实现的。本发明公开了一种基于自适应终端滑模控制的汽车线控转向控制方法，包括前轮转角δf和方向盘转角θh的实时信号采集，其主要步骤如下：

步骤1，令汽车线控转向系统的伺服驱动器运行在转矩控制模式，实时采集前轮转角δf和方向盘转角θh；

步骤2，根据步骤1所得的前轮转角δf和方向盘转角θh，定义跟踪误差e＝δf-θhr，其中θhr为方向盘转动参考角，nθ是方向盘转角θh和前轮转角δf之间的比例因子；

步骤3，将步骤1采集到的前轮转角δf通过一阶微分得到前轮转角角速度将步骤2得到的跟踪误差e通过一阶微分得到跟踪误差一阶微分值

步骤4，将步骤2得到的跟踪误差e、步骤3得到的跟踪误差一阶微分值给到终端滑模平面上，得到终端滑模变量s；

所述终端滑模变量s被定义为：

且2q>p

式中，λ为终端滑模参数1且它是一个正数，q为终端滑模参数2且它是一个正奇数，p为终端滑模参数3且它是一个正奇数；

步骤5，首先给定二个汽车线控转向系统参数标称值并分别记为汽车线控转向系统参数标称值a、汽车线控转向系统参数标称值b，然后，对汽车线控转向系统参数标称值a通过一阶微分得到一阶微分值并将一阶微分值的上界值记为ρ，即

步骤6，将步骤1得到的前轮转角δf、步骤3得到的前轮转角角速度和跟踪误差一阶微分值步骤4得到的终端滑模变量s通过自适应律得到汽车线控转向系统不确定参数和扰动值τfea的上界估计值汽车线控转向系统参数标称值a的上界估计值汽车线控转向系统参数标称值b的上界估计值汽车线控转向系统参数标称值a的一阶微分值的上界值ρ的估计值

步骤7，将步骤1得到的前轮转角δf、步骤2得到的跟踪误差一阶微分值步骤4得到的终端滑模变量s、步骤6得到的汽车线控转向系统不确定参数和扰动值τfea的上界估计值汽车线控转向系统参数标称值a的上界估计值汽车线控转向系统参数标称值b的上界估计值汽车线控转向系统参数标称值a的一阶微分值的上界估计值作为输入变量输入到自适应终端滑模控制器中，得到控制器输出信号u；

u＝us-k1sign(s)-k2s

式中，

k1为终端滑模控制器趋近律参数1且是一个正数；

k2为终端滑模控制器趋近律参数2且是一个正数；

us为终端滑模控制器中间控制律，其表达式为：

式中，sat(s)为饱和函数，表达式为δ表示终端滑模边界层厚度，为方向盘转动参考角的角加速度的上界值；

步骤8，将步骤7中的控制器输出信号u传送到转向电机伺服驱动器中给汽车线控转向设备发送电压指令，控制车轮转动，得到理想前轮转角δ′f。

优选的，步骤1所述实时采集的采样周期为t＝10ms。

优选的，步骤6所述汽车线控转向系统不确定参数和扰动值τfea的上界估计值的表达式如下：

式中，

为汽车线控转向系统不确定参数和扰动值的上界估计值的系数1，其表达式为其中，为的一阶微分值，其表达式为η1为自适应律调整比例参数1且是一个正数，σc0为汽车线控转向系统不确定参数和扰动值的上界估计值的系数1即的终端滑模变量调整参数，且σc0>0；

为汽车线控转向系统不确定参数和扰动值的上界估计值的系数2，其表达式为其中，为一阶微分值，其表达式为η2为自适应律调整比例参数2且是一个正数，σc1为汽车线控转向系统不确定参数和扰动值的上界估计值的系数2即的终端滑模变量调整参数，且σc1>0；

为汽车线控转向系统不确定参数和扰动值的上界估计值的系数3，其表达式为其中，为一阶微分值，其表达式为η3为自适应律调整比例参数3且是一个正数，σc2为汽车线控转向系统不确定参数和扰动值的上界估计值的系数3即的终端滑模变量调整参数，且σc2>0。

优选的，步骤6所述汽车线控转向系统参数标称值a的上界估计值的计算如下：

其中，为的一阶微分值，其表达式为：

式中，η4为自适应律调整比例参数4且是一个正数，为方向盘转动参考角的角加速度的上界值,σa1为汽车线控转向系统参数标称值a的上界估计值的终端滑模变量调整参数，且σa1>0。

优选的，步骤6所述汽车线控转向系统参数标称值b的上界估计值的计算如下：

其中，为的一阶微分值，其表达式为：

式中，η5为自适应律调整比例参数5且是一个正数，σb1为汽车线控转向系统参数标称值b的上界估计值的终端滑模变量调整参数，且σb1>0。

优选的，步骤6所述汽车线控转向系统参数标称值a的一阶微分值的上界值ρ的估计值的计算如下：

其中，为的一阶微分值，其表达式为式中，η6为自适应律调整比例参数6且是一个正数，σρ为汽车线控转向系统参数标称值a的一阶微分值的上界值ρ的估计值的终端滑模变量调整参数，且σρ>0。

本发明公开的基于自适应终端滑模控制的汽车线控转向控制方法，在系统参数未知和道路条件不同的情况下，实现了前轮转角密切跟踪方向盘转动参考角度的性能，具有很强的稳定性和鲁棒性，其有益效果具体体现在：

1.所提出的基于自适应终端滑模控制的汽车线控转向控制方法优于传统的基于超平面的线性滑模控制，能保证误差能在有限时间内收敛，具有很好的稳定性；

2.自适应律对系统参数不确定性和变化的行驶条件具有强鲁棒性，无需提前知晓系统参数和道路信息；

3.采用边界层方法克服了闭环系统抖振现象。

附图说明

图1是本发明的汽车线控转向系统控制结构图。

图2是本发明控制方法在斜坡转向测试中的跟踪性能曲线图。

图3是本发明控制方法在斜坡转向测试中的控制扭矩曲线图。

图4是本发明控制方法在斜坡转向测试中的系统参数估计值曲线图。

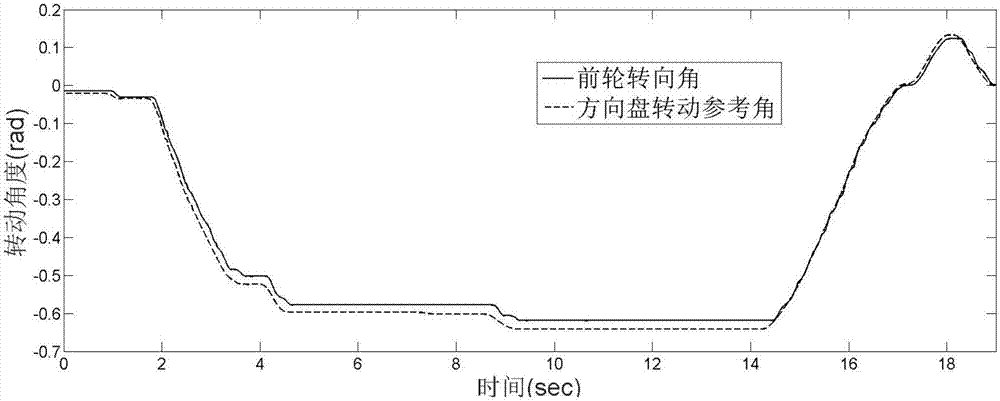
图5是本发明控制方法在双移线测试中的跟踪性能曲线图。

图6是本发明控制方法在双移线测试中的控制扭矩曲线图。

图7是本发明控制方法在双移线测试中的系统参数估计值曲线图。

具体实施方式

下面将结合附图对本发明的技术方案进行清楚、完整的描述。

参见图1。由该图可见，本发明所述基于自适应终端滑模控制的汽车线控转向控制方法，包括前轮转角δf和方向盘转角θh的实时信号采集，主要步骤如下：

步骤1，令汽车线控转向系统的伺服驱动器运行在转矩控制模式，实时采集前轮转角δf和方向盘转角θh。本实施例中，采样周期t＝10ms。

步骤2，根据步骤1所得的前轮转角δf和方向盘转角θh，定义跟踪误差e＝δf-θhr，其中θhr为方向盘转动参考角，nθ是方向盘转角θh和前轮转角δf之间的比例因子。在本实施例中，nθ＝12。

步骤3，将步骤1采集到的前轮转角δf通过一阶微分得到前轮转角角速度将步骤2得到的跟踪误差e通过一阶微分得到跟踪误差一阶微分值

步骤4，将步骤2得到的跟踪误差e、步骤3得到的跟踪误差一阶微分值给到终端滑模平面上，得到终端滑模变量s。

所述终端滑模变量s被定义为：

且2q>p

式中，λ为终端滑模参数1且它是一个正数，q为终端滑模参数2且它是一个正奇数，p为终端滑模参数3且它是一个正奇数。在本实施例中，λ＝8，p＝7，q＝5。

步骤5，首先给定二个汽车线控转向系统参数标称值并分别记为汽车线控转向系统参数标称值a、汽车线控转向系统参数标称值b，然后，对汽车线控转向系统参数标称值a通过一阶微分得到一阶微分值并将一阶微分值的上界值记为ρ，即

步骤6，将步骤1得到的前轮转角δf、步骤3得到的前轮转角角速度和跟踪误差一阶微分值步骤4得到的终端滑模变量s通过自适应律得到汽车线控转向系统不确定参数和扰动值τfea的上界估计值汽车线控转向系统参数标称值a的上界估计值汽车线控转向系统参数标称值b的上界估计值汽车线控转向系统参数标称值a的一阶微分值的上界值ρ的估计值

步骤7，将步骤1得到的前轮转角δf、步骤2得到的跟踪误差一阶微分值步骤4得到的终端滑模变量s、步骤6得到的汽车线控转向系统不确定参数和扰动值τfea的上界估计值汽车线控转向系统参数标称值a的上界估计值汽车线控转向系统参数标称值b的上界估计值汽车线控转向系统参数标称值a的一阶微分值的上界估计值作为输入变量输入到自适应终端滑模控制器中，得到控制器输出信号u。

u＝us-k1sign(s)-k2s

式中，

k1为终端滑模控制器趋近律参数1且是一个正数；

k2为终端滑模控制器趋近律参数2且是一个正数；

us为终端滑模控制器中间控制律，其表达式为：

式中，sat(s)为饱和函数，表达式为δ表示终端滑模边界层厚度，为方向盘转动参考角的角加速度的上界值。

在本实施例中，k1＝0.01，k2＝3.5，δ＝0.3。

步骤8，将步骤7中的控制器输出信号u传送到转向电机伺服驱动器中给汽车线控转向设备发送电压指令，控制车轮转动，得到理想前轮转角δ′f。

在步骤6中涉及的的具体计算如下。

1、步骤6所述汽车线控转向系统不确定参数和扰动值τfea的上界估计值的表达式如下：

式中，

为汽车线控转向系统不确定参数和扰动值的上界估计值的系数1，其表达式为其中，为的一阶微分值，其表达式为η1为自适应律调整比例参数1且是一个正数，σc0为汽车线控转向系统不确定参数和扰动值的上界估计值的系数1即的终端滑模变量调整参数，且σc0>0。在本实施例中，η1＝1000，σc0＝0.001。

为汽车线控转向系统不确定参数和扰动值的上界估计值的系数2，其表达式为其中，为一阶微分值，其表达式为η2为自适应律调整比例参数2且是一个正数，σc1为汽车线控转向系统不确定参数和扰动值的上界估计值的系数2即的终端滑模变量调整参数，且σc1>0。在本实施例中，η2＝500，σc1＝0.002。

为汽车线控转向系统不确定参数和扰动值的上界估计值的系数3，的表达式为其中，为一阶微分值，其表达式为η3为自适应律调整比例参数3且是一个正数，σc2为汽车线控转向系统不确定参数和扰动值的上界估计值的系数3即的终端滑模变量调整参数，且σc2>0。在本实施例中，η3＝500，σc2＝0.001。

2、步骤6所述汽车线控转向系统参数标称值a的上界估计值的计算如下：

其中，为的一阶微分值，其表达式为：

式中，η4为自适应律调整比例参数4且是一个正数，为方向盘转动参考角的角加速度的上界值,σa1为汽车线控转向系统参数标称值a的上界估计值的终端滑模变量调整参数，且σa1>0。在本实施例中，η4＝500，σa1＝0.0005，

3、步骤6所述汽车线控转向系统参数标称值b的上界估计值的计算如下：

其中，为的一阶微分值，其表达式为：

式中，η5为自适应律调整比例参数5且是一个正数，σb1为汽车线控转向系统参数标称值b的上界估计值的终端滑模变量调整参数，且σb1>0。在本实施例中，η5＝500，σb1＝0.0005.。

4、步骤6所述汽车线控转向系统参数标称值a的一阶微分值的上界值ρ的估计值的计算如下：

其中，为的一阶微分值，式中，η6为自适应律调整比例参数6且是一个正数，σρ为汽车线控转向系统参数标称值a的一阶微分值的上界值ρ的估计值的终端滑模变量调整参数，且σρ>0。在本实施例中，η6＝500，σρ＝0.0025。

参见图2、图3、图4、图5、图6、图7，为验证本发明的实施效果，在汽车线控转向系统实验平台中得到如图所示的控制效果图，图2、图3、图4为斜坡转向测试得到的曲线图，图5、图6、图7为双移线测试得到的曲线图，从六张图中可看出本发明的控制方法可以使得前轮转角密切跟踪方向盘转动参考角度，减小了跟踪误差，改善了抖振现象，增强了鲁棒性，同时各系统参数分别收敛至某个常数确保了闭环系统的稳定性。