一种基于变时间间距策略的异构车队容错控制方法与流程

本发明涉及异构车队控制技术领域，具体而言，尤其涉及一种基于变时间间距策略的异构车队容错控制方法。

背景技术：

近年来，自主车队的纵向控制得到了深入研究，zhengy等研究了异构车队信息流动协议问题，并利用精确反馈线性化建立线性化车辆动力学模型，最后利用代数图论和routh-hurwitz稳定性判据证明了异构车队的稳定性。但针对模型或者外界干扰不确定的非线性系统，反馈线性化不能提供有效的设计方法，即不能满足解决环境和系统动态特性不完备条件下的控制问题。为此很多学者提出了基于非线性的车队控制方法，如yuew等研究了协同自适应巡航控制系统的非线性控制，针对传感器失效的情况提出了切换控制器设计方法，从而实现了个体车辆的稳定性和车队的队列稳定性。高峰等研究了带有时延的非线性车队控制问题，并利用滑模控制器和比例积分微分控制器，根据队列稳定性判据，分别对两种控制器进行分析验证，最后得出了比例积分微分控制器具有更强的迟滞鲁棒性的结论。但大部分文献并没有考虑执行器故障的情况。然而，在实际车队控制系统中，执行器故障是经常存在的，会导致系统的性能下降甚至不稳定，因此，关于车队控制系统的容错控制研究具有极其重要的研究价值和实际意义。郭祥贵等人运用自适应增益的补偿控制律，模糊逼近技术和滑模控制方法设计出了自适应模糊容错控制器，使高速列车在执行器故障的情况下，不仅能保证单车稳定，还能保证队列稳定。通过建立李雅普诺夫函数，证明了车辆的有限时间稳定性和车队的队列稳定性。

针对车队控制系统存在执行器故障的问题研究相对较少，虽然郭祥贵等人提出了自适应容错控制，但研究成果是基于固定时间间距策略，其不能保证交通流量稳定性，因此本发明提出了变时间间距策略。另外，在郭祥贵等人的研究中，所有的车辆假设为同一规格，这明显的减少了技术的难度，也限制了实际的应用，因此本发明将对异质车队控制进行研究。

技术实现要素：

根据上述提出考虑到固定间距策略不能保证队列稳定，固定时间间距策略不能保证交通流量稳定性，非零的初始间距误差可能造成系统不稳定的技术问题，而提供一种基于变时间间距策略的异构车队容错控制方法。本发明提出的变时间间距策略，相比于传统的变时间间距策略，其不仅能解决非零间距误差的问题，而且还可以增加临界交通容量。

本发明采用的技术手段如下：

一种基于变时间间距策略的异构车队容错控制方法，包括如下步骤：

s1、对车辆纵向运动进行受力分析，并结合执行器故障模型，建立执行器故障下的车辆纵向动力学模型；

s2、根据车辆自身信息，构造带有故障信息下界的变时间间距策略；

s3、基于步骤s2中构造的变时间间距策略，建立比例积分微分滑模面和耦合滑模面；

s4、基于步骤s3建立的比例积分微分滑模面和耦合滑模面，选取合适的李雅普诺夫函数，设计容错控制器和自适应更新率，并证明系统的有限时间稳定性。

进一步地，所述步骤s4之后还包括：

s5、基于步骤s2中的带有故障信息下界的变时间间距策略，证明交通流量稳定性。

s6、基于步骤s3中的比例积分微分滑模面和耦合滑模面，证明车队的队列稳定性。

进一步地，所述步骤s1的具体过程如下：

s11、定义领头车辆的动态模型，如下所示：

其中，x0(t)、v0(t)、a0(t)分别表示领头车的位置、速度、加速度，另外a0(t)表示同一个给定的时间函数；

s12、对车辆纵向运动进行受力分析，获得车辆纵向动力学模型：

其中，xi,vi,ai分别是车辆i的位置、速度、加速度；ci是执行器输入，fi(vi,ai)是非线性函数，其函数表达式如下：

其中，τi是发动机时间常数，υ是空气质量常数，mi，ai，cdi和dmi分别是车辆i的质量，横截面积，拽力系数和机械拽力；

s13、结合执行器故障模型，建立执行器故障下的车辆纵向动力学模型；

所述执行器故障模型具体为：

uai＝ρi(t，tρi)ui+ri(t，tri)

其中，uai是执行器故障下的控制输入，ρi(t,tρi)代表执行器的效率故障，ri(t,tri)代表执行器的偏置故障，tρi和tri分别代表效率故障和偏置故障发生的时间；

将所述执行器故障模型带入到所述车辆纵向动力学模型，得到所述执行器故障下的车辆纵向动力学模型如下：

其中，xi,vi,ai分别是第i辆车的位置、速度、加速度。

进一步地，所述步骤s2的具体过程如下：

s21、定义位移跟踪误差，如下：

其中，δi为第i辆车与第i-1辆车的安全间距误差，γi是一个正常数，li是车辆i的长度，δi-1,i是两车之间的安全距离，h代表车队控制系统的延迟时间，σ代表安全系数，am是被控车辆期望的最大加速度，ρi0代表执行器故障的下界值；从而可以得出：

表示提出的变时间间距策略的初始值在任何情况下都是零；

s22、定义理想的车间距离，如下：

进一步地，所述步骤s3的具体过程如下：

s31、为了使δi在有限时间内趋近于无限接近于0并且保证队列的一致稳定性，构造比例积分微分滑模面：

其中，kp,ki,kd分别代表比例、积分、微分系数；

s32、根据传递函数gi(s)的定义，构建δi和δi+1的之间的关系，定义耦合滑模面：

其中，λ是耦合滑模面si和si+1的正常数；当si到达滑模表面时，si也能到达滑模表面。

进一步地，所述步骤s4的具体过程如下：

s41、采用模糊逻辑技术逼近未知的非线性函数，其函数表达式如下：

其中，是未知的，代表加权矩阵的最优向量；代表实矩阵；m代表模糊规则的个数；bi代表模糊系统的输入；代表模糊系统的径向基函数；代表径向基函数的重构误差，满足其中是未知的正常数；

s42、设计自适应误差，具体为：

式中，是ψi^*的估计误差，是ηi^*的估计误差；

s43、设计自适应更新律，具体为：

s44、结合滑模控制方法和模糊逼近技术，同时采用自适应方法对整个闭环系统进行处理，得到自适应模糊容错控制器，具体为：

其中，1≤1/ρi0≤λi，θi和ζi代表正常数，ki1代表控制器的增益，zi表示为：

s45、为了证明系统的有界性，构造lyapunov函数，其函数表达式如下：

对所述lyapunov函数求导，并将间距误差、耦合滑模面、自适应更新率和控制律所带入lyapunov函数求导后的公式，得到：

根据lyapunov稳定理论，得到闭环系统中的所有信号均最终一致有界，其中：

进一步地，所述步骤s5的具体过程如下：

s51、基于步骤s2中的带有故障信息下界的变时间间距策略，假设在稳定的状态下，第i辆跟随车的间距squad,i＝squad和速度vi＝v，在稳定的状态下γi＝0，得到：

交通密度：

s52、定义流量速率：

s53、为了分析整个车队的队列稳定性，计算再令计算临界交通密度：

s54、利用与步骤s51-s53相同的方法，得出传统变时间间距策略的临界交通密度：

s55、比较步骤s53和s54计算的临界交通密度，证明基于步骤s2中的带有故障信息下界的变时间间距策略可以提高临界交通密度。

进一步地，所述步骤s6的具体过程如下：

因为si＝λsi-si+1在有限时间内趋于无限接近于0域附近，可以得到的关系如下：

对上式的两边进行拉普拉斯变换，可得：

所以可得：gi(s)＝δi+1(s)/δi(s)＝λ，证明如果0＜λ≤1，整个车队的队列稳定性将被满足。

进一步地，所述步骤s6之后还包括：

s7、对采用基于变时间间距策略的异构车队容错控制方案的故障下的车辆纵向动力学模型、比例积分微分滑模面和耦合滑模面、容错控制器和自适应更新率进行仿真验证研究，与常规手段进行对比，进一步验证有效性和优越性。

较现有技术相比，本发明具有以下优点：

1、本发明提出的变时间间距策略不仅能保证队列稳定性，而且能保证交通流量稳定性。并且相比于传统的变时间间距策略，其不仅移除了零初始间距误差的假设，而且可以增加临界交通容量。

2、本发明针对异质车队系统环境下存在执行器故障的情况，同时考虑到模型参数的不确定性和外界扰动的影响，建立了带有执行器故障的非线性模型，设计了异质车队控制系统环境下的自适应容错控制，使车队能够在执行器故障的情况下正常的运行。

3、本发明考虑了执行器故障发生的情况，建立了包含故障信息的lyapunov函数，基于滑模控制方法和自适应补偿技术，得到了整个闭环系统有限时间稳定的条件。

基于上述理由本发明可在异构车队等领域广泛推广。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图做以简单地介绍，显而易见地，下面描述中的附图是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动性的前提下，还可以根据这些附图获得其他的附图。

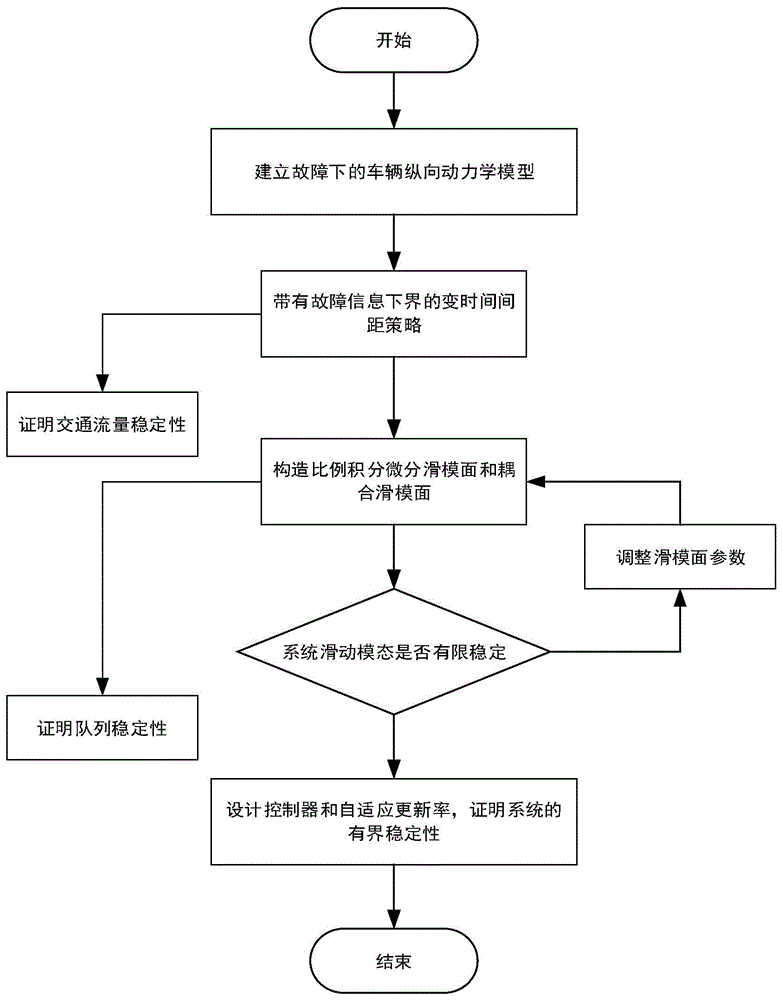
图1为本发明方法流程图。

图2为本发明实施例提供的异质车队示意图。

图3为本发明实施例提供的间距误差仿真图。

图4为本发明实施例提供的速度仿真图。

图5为本发明实施例提供的加速度仿真图。

图6为本发明实施例提供的滑膜面仿真图。

图7为本发明实施例提供的自适应律仿真图。

图8为本发明实施例提供的自适应律仿真图。

具体实施方式

为了使本技术领域的人员更好地理解本发明方案，下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分的实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都应当属于本发明保护的范围。

需要说明的是，本发明的说明书和权利要求书及上述附图中的术语“第一”、“第二”等是用于区别类似的对象，而不必用于描述特定的顺序或先后次序。应该理解这样使用的数据在适当情况下可以互换，以便这里描述的本发明的实施例能够以除了在这里图示或描述的那些以外的顺序实施。此外，术语“包括”和“具有”以及他们的任何变形，意图在于覆盖不排他的包含，例如，包含了一系列步骤或单元的过程、方法、系统、产品或设备不必限于清楚地列出的那些步骤或单元，而是可包括没有清楚地列出的或对于这些过程、方法、产品或设备固有的其它步骤或单元。

如图1所示，本发明提供了一种基于变时间间距策略的异构车队容错控制方法，包括如下步骤：

s1、对车辆纵向运动进行受力分析，并结合执行器故障模型，建立执行器故障下的车辆纵向动力学模型；

s2、根据车辆自身信息，构造带有故障信息下界的变时间间距策略；

s3、基于步骤s2中构造的变时间间距策略，建立比例积分微分滑模面和耦合滑模面；

s4、基于步骤s3建立的比例积分微分滑模面和耦合滑模面，选取合适的李雅普诺夫函数，设计容错控制器和自适应更新率，并证明系统的有限时间稳定性。

s5、基于步骤s2中的带有故障信息下界的变时间间距策略，证明交通流量稳定性。

s6、基于步骤s3中的比例积分微分滑模面和耦合滑模面，证明车队的队列稳定性。

实施例1

步骤s1的具体过程如下：

s11、定义领头车辆的动态模型，如下所示：

其中，x0(t)、v0(t)、a0(t)分别表示领头车的位置、速度、加速度，另外a0(t)表示同一个给定的时间函数；

s12、对车辆纵向运动进行受力分析，获得车辆纵向动力学模型：

其中，xi,vi,ai分别是车辆i的位置、速度、加速度；ci是执行器输入，fi(vi,ai)是非线性函数，其函数表达式如下：

其中，τi是发动机时间常数，υ是空气质量常数，mi，ai，cdi和dmi分别是车辆i的质量，横截面积，拽力系数和机械拽力；由于车的质量mi不确定，因此非线性函数fi(vi,ai)应该是未知的，我们选择模糊逼近技术来逼近未知的非线性函数fi(vi,ai)。

s13、结合执行器故障模型，建立执行器故障下的车辆纵向动力学模型；

所述执行器故障模型具体为：

uai＝ρi(t，tρi)ui+ri(t，tri)

其中，uai是执行器故障下的控制输入，ρi(t,tρi)代表执行器的效率故障，ri(t,tri)代表执行器的偏置故障，tρi和tri分别代表效率故障和偏置故障发生的时间；

将所述执行器故障模型带入到所述车辆纵向动力学模型，得到所述执行器故障下的车辆纵向动力学模型如下：

其中，xi,vi,ai分别是第i辆车的位置、速度、加速度。

实施例2

在实施例1的基础上，步骤s2的具体过程如下：

s21、定义位移跟踪误差，如下：

其中，δi为第i辆车与第i-1辆车的安全间距误差，γi是一个正常数，li是车辆i的长度，δi-1,i是两车之间的安全距离，h代表车队控制系统的延迟时间，σ代表安全系数，am是被控车辆期望的最大加速度，ρi0代表执行器故障的下界值；从而可以得出：

表示提出的变时间间距策略的初始值在任何情况下都是零；

s22、定义理想的车间距离，如下：

实施例3

在实施例2的基础上，步骤s3的具体过程如下：

s31、为了使δi在有限时间内趋近于无限接近于0并且保证队列的一致稳定性，构造比例积分微分滑模面：

其中，kp,ki,kd分别代表比例、积分、微分系数；

s32、根据传递函数gi(s)的定义，构建δi和δi+1的之间的关系，定义耦合滑模面：

其中，λ是耦合滑模面si和si+1的正常数；当si到达滑模表面时，si也能到达滑模表面。

实施例4

在实施例3的基础上，步骤s4的具体过程如下：

s41、采用模糊逻辑技术逼近未知的非线性函数，其函数表达式如下：

其中，是未知的，代表加权矩阵的最优向量；代表实矩阵；m代表模糊规则的个数；bi代表模糊系统的输入；代表模糊系统的径向基函数；代表径向基函数的重构误差，满足其中是未知的正常数；

s42、设计自适应误差，具体为：

式中，是ψi^*的估计误差，是ηi^*的估计误差；

s43、设计自适应更新律，具体为：

s44、结合滑模控制方法和模糊逼近技术，同时采用自适应方法对整个闭环系统进行处理，得到自适应模糊容错控制器，具体为：

其中，1≤1/ρi0≤λi，θi和ζi代表正常数，ki1代表控制器的增益，zi表示为：

s45、为了证明系统的有界性，构造lyapunov函数，其函数表达式如下：

对所述lyapunov函数求导，并将间距误差、耦合滑模面、自适应更新率和控制律所带入lyapunov函数求导后的公式，得到：

根据lyapunov稳定理论，得到闭环系统中的所有信号均最终一致有界，其中：

实施例5

在实施例4的基础上，步骤s5的具体过程如下：

s51、基于步骤s2中的带有故障信息下界的变时间间距策略，假设在稳定的状态下，第i辆跟随车的间距squad,i＝squad和速度vi＝v，在稳定的状态下γi＝0，得到：

交通密度：

s52、定义流量速率：

s53、为了分析整个车队的队列稳定性，计算再令计算临界交通密度：

s54、利用与步骤s51-s53相同的方法，得出传统变时间间距策略的临界交通密度：

s55、比较步骤s53和s54计算的临界交通密度，证明基于步骤s2中的带有故障信息下界的变时间间距策略可以提高临界交通密度。

实施例6

在实施例5的基础上，步骤s6的具体过程如下：

因为si＝λsi-si+1在有限时间内趋于无限接近于0域附近，可以得到的关系如下：

对上式的两边进行拉普拉斯变换，可得：

所以可得：gi(s)＝δi+1(s)/δi(s)＝λ，证明如果0＜λ≤1，整个车队的队列稳定性将被满足。

实施例7

在实施例1-5的基础上，还包括：

s7、对采用基于变时间间距策略的异构车队容错控制方案的故障下的车辆纵向动力学模型、比例积分微分滑模面和耦合滑模面、容错控制器和自适应更新率进行仿真验证研究，与常规手段进行对比，进一步验证有效性和优越性。

为了验证本实施例提供的基于变时间间距策略的自适应模糊容错控制方法的有效性，采用matlab进行仿真实验验证，并作出详细的说明。

如图2所示，为本实施例提供的异构车队模型，综合考虑执行器故障和外界干扰，采用了滑模技术和模糊逻辑逼近技术，设计出了容错控制器，能使得闭环系统有限时间稳定，具有良好的位置，速度，加速度跟踪性能，且对执行器故障具有一定的鲁棒性，对外界干扰具有良好的抑制性。

具体的，本实施例中，假设有一辆领头车和六辆跟随车在车道上直线行驶，领头车的加速度为：

在仿真中设置安全距离δi-1,i＝7m，延迟时间h＝0.08s，安全系数σ＝0.4，最大加速度am＝3.5m/s²，空气质量常数υ＝1.2kg/m³，车辆的横截面积ai＝2.2m²，拽力系数cdi＝0.35，机械拽力dmi＝5n；考虑干扰wi(t)＝0.1sin(t)，对于每一辆车辆，设置规则数为mi＝20，bi＝vi，模糊隶属度函数设置为：

考虑到由于执行器故障的实际输入uai＝ρi(t)ui(t)+ri(t)，其中，设置ρi(t)＝0.75+0.25sin(0.1it)，ri(t)＝0.1sin(t)，假设故障的下界ρi0＝0.5，利用关系1≤1/ρi0≤λi，可以得到λi≥2。另外六辆跟随车的质量mi分别为[1500，1600，1550，1650，1500，1400]，发动机时间常数τi分别为[0.1，0.3，0.2，0.4，0.25，0.4]，车长li分别为[4，4.5，5，5，4.5，3.5]；

最后在仿真中，整个车队包括一辆领头车和六辆跟随车的初始状态如下：初始位置xi(0)(m)＝[150，135，125.5，112.5，99.5，87，75.5]；初始速度vi(0)(m/s)＝[1，4，2，0，5，3，1]，初始加速度ai(0)(m/s²)＝[0，1，5，2，1，3，1]。

基于上述参数，对本发明提出的基于变时间间距策略的自适应模糊容错控制方法进行仿真验证如图3-8所示。其中，图3显示车间距离误差依次的递减，并且最终收敛到接近0附近，车队可以保证实现有限时间稳定和队列稳定；图4显示跟随车的速度跟随领头车的速度，并逐渐的收敛到期望的速度；图5显示了加速度跟踪曲线，最大的加速度小于设定的加速度，满足燃油经济的特性；图6显示了滑模曲线逐渐趋于接近0附近，并且最后抖振几乎完全消失；图7和图8显示了自适应参数逐渐趋于稳定的常数。至此完成了算法的数字仿真，验证了其有效性。

上述本发明实施例序号仅仅为了描述，不代表实施例的优劣。

在本发明的上述实施例中，对各个实施例的描述都各有侧重，某个实施例中没有详述的部分，可以参见其他实施例的相关描述。

最后应说明的是：以上各实施例仅用以说明本发明的技术方案，而非对其限制；尽管参照前述各实施例对本发明进行了详细的说明，本领域的普通技术人员应当理解：其依然可以对前述各实施例所记载的技术方案进行修改，或者对其中部分或者全部技术特征进行等同替换；而这些修改或者替换，并不使相应技术方案的本质脱离本发明各实施例技术方案的范围。